大跨度屋盖抗风设计背景效应分析

根据上节的分析可知，背景效应是联系基准响应与背景响应的桥梁，主要表现为相关性效应。实际的脉动风荷载是非完全相关的，在时域上表现为风压力时程的非同步性，在频域上表现为风压力互功率谱的部分相干性。这种非完全相关脉动荷载作用在“刚性”结构上，产生的准静力响应与脉动风荷载的互统计量有较大的关联。不仅如此，不同结构形式对部分相关脉动荷载的敏感性也有所不同。本节首先分析不同结构形式对非完全相关荷载准静力效应的敏感程度，进而结合时域相关性与频域相干性的联系，给出背景效应系数μc关于风压谱参数的半理论公式。

荷载的相关性效应必须体现在多自由度结构中，双自由度体系是最为简单的多自由度分析系统，能够较好地反映不同类型、典型大跨度屋盖结构的静力和动力特性，能够直观地将结构进行有效分类并进行概念性的延伸，便于寻求结构背景效应的概念性规律。因此，为研究不同形式的结构在不同相关性荷载作用下准静力响应的变化规律，本节选取简化的双自由度结构，变化作用在两个自由度上脉动荷载的相关性，考察结构响应的背景效应系数μc。

典型的大跨度结构，从形状上可以分为平面和曲面两大类，为了从概念上分析荷载相关性效应，本节选取的简化双自由度体系分析算例如图5-2所示。图中黑色实线代表简化的双自由度结构，黑色圆点代表自由度所在的质量元。结构的坐标系定义如下，沿结构方向（切向）为坐标，垂直于结构方向（法向）为自由度位移方向x。假设切向变形可忽略，因此，结构两个自由度分别为两个质量元的法向运动x1和x2。假设结构具有对称性，质量矩阵为单位矩阵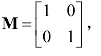结构具有对称模态和反对称模态对应的自振频率分别为ωs和ωa。结构刚度矩阵为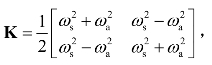其逆矩阵柔度矩阵为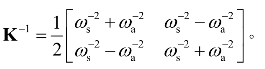可见，当刚度矩阵非主对角元素为正，即某以自由度上施加正向力，另一自由度上的位移为同向时，对称模态的阶数较小，即ωs＜ωa时，这类结构一般是平面类的，如梁、板、网架类结构，如图5-2a所示。另一类结构，当在某一自由度上施加正向力时，另一自由度上的位移为反向，刚度矩阵非对角元素为负，此时，反对称模态更容易发生，即ωs＞ωa，这类结构一般为曲面结构，如拱、壳类结构，如图5-2b所示。

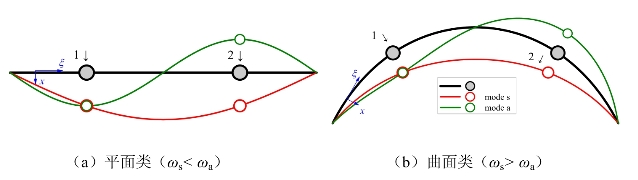
图5-2　两种典型的双自由度体系简图

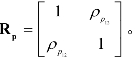假设作用在两个自由度上的脉动风荷载均方根分别为和即脉动风荷载均方根向量两个自由度上的脉动风荷载相关系数为即脉动风荷载相关系数矩阵根据背景响应的定义式（4-4）可得两个自由度上的背景响应为，

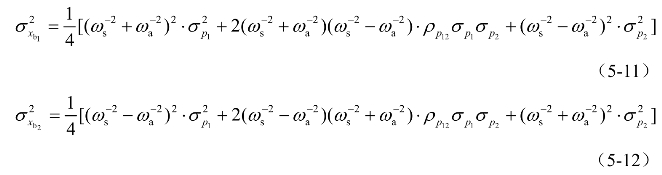
根据基准响应定义式（5-5），可得两个自由度上的基准响应为，

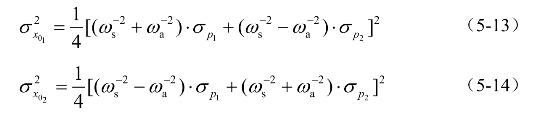
根据背景效应系数的定义，可得

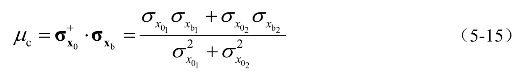
特别地，当两个自由度上的脉动荷载均方根相等，即时，式（5-15）可简化为，

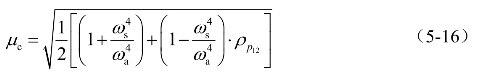
可以发现，对于不同结构形式，背景效应系数μc随脉动荷载相关性变化趋势主要与结构对称模态与反对称模态的频率比ωs/ωa有关。在不同频率比ωs/ωa下，结构背景效应系数μc 随脉动荷载相关系数的变化趋势如图5-3所示。

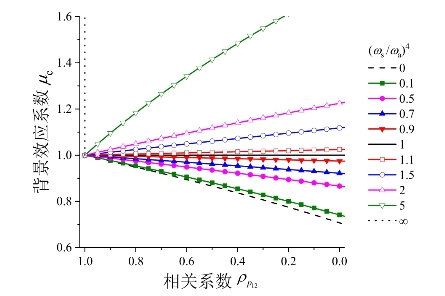
图5-3　背景效应系数随脉动荷载相关性的变化

由图5-3可以看出，对于对称模态起主导作用的平面类结构形式，背景效应系数一般小于1，称为背景折减效应。这种效应不仅局限在对称结构的情况，同样适用于同号模态起主导作用的结构，如悬挑结构（高层结构也属于这个范畴）。这是由于在同号模态上，非同步荷载可以看作是互相抵消的作用，这种作用随着脉动荷载相关性减弱而增强。而对于反对称（变号）模态为低阶的曲面类结构形式，背景效应系数可能大于1，称为背景放大效应。这是因为作用在变号模态上，同步性反而是一种抵消效应，非同步性可能放大变号模态的振动，这种效应很可能随着相关性减弱而增强。由于脉动荷载均方根相等，所以在当反对称模态绝对占优的情况（ωs/ωa→∞），表达式出现了奇异的情形，是由于在这种情况下，基准响应很小，远小于任意非完全相关荷载作用下的背景响应。在实际中，这种情况是不存在的。

针对一般的σp1≠σp2情况，可将式（5-11）至式（5-14）直接代入式（5-15）。图5-4a给出了（或1/2）时结构背景效应系数μc随脉动荷载相关系数变化趋势。由图可知，对于上述两种类型结构，结构背景效应系数μc随脉动荷载相关系数变化趋势与脉动荷载均方根相等时基本一致，曲面类结构背景放大效应程度减弱，上文提到的奇异的情形消失。这是因为曲面类结构对荷载的对称性较为敏感，当脉动荷载统计值完全对称时，结构的基准响应中反对称模态的分量接近于零，导致背景放大效应的奇异现象；而当脉动荷载统计值由对称变为非对称时，结构的基准响应中反对称模态的分量增加，使得背景放大效应程度减弱。在不同比值下，背景效应系数μc的取值范围在频率比ωs/ωa→0时最小，此时结构振动完全为“同号”模态，背景折减效应达到极致。当ωs/ωa→∞时，结构振动完全为“变号”模态，背景放大效应达到最大。不同比值下的这两个极限情况的背景效应系数μc随脉动荷载相关系数变化趋势如图5-4b所示。由图可知，脉动荷载均方根分布对称性越强，背景效应越显著，背景效应系数μc的取值越偏离1。特别地，当脉动荷载均方根相差悬殊，即时，背景效应系数μc取值趋于1。(www.xing528.com)

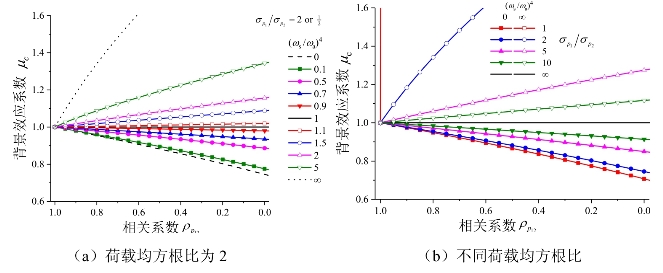
图5-4　不对称均方根脉动荷载作用下背景效应系数随脉动荷载相关性的变化

由上面分析可知，背景效应系数μc和脉动荷载的相关系数关系十分密切。因此，要建立背景效应系数与风压谱参数的联系，还需要讨论脉动荷载的相关系数与风压谱参数的关系，即建立时域相关性与频域相干性的联系。

根据脉动荷载的相关系数ρp12的定义，代入简化滤波表示的互功率谱模型式（4-12），可得，

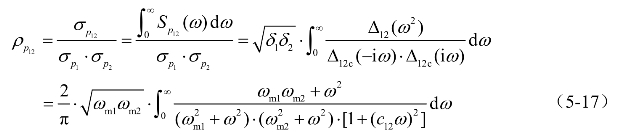
根据闭路积分原理可得到该积分的解析表达式，

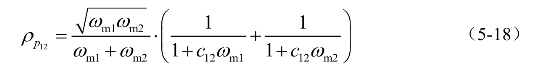
该式表达了时域相关性与频域相干性的联系，可以发现，两点脉动风压时程的相关系数不仅与描述互功率谱滤波相干系数有关，还与自功率谱的峰值频率ωm1、ωm2密切相关。下面将对其中的参数进行讨论。

当滤波相干系数c12=0时，两点风压时程的相关系数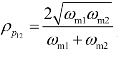为两点脉动风压自功率谱的峰值频率几何平均值与代数平均值之比。仅当两点脉动风压自功率谱的峰值频率相等，即ωm1=ωm2=ωm时，相关系数即完全相关。当峰值频率相差悬殊，即ωm1/ωm2→0或ωm1/ωm2→∞时，有即完全无关。一般地，当两点距离很小时，D12≈0，c12≈0，若两点处于流场中流动状态较为稳定的区域，ωm1≈ωm2，脉动风压力的相关性接近完全相关；而当两点恰好处于流场中发生转变的区域，峰值频率相差较大，即便两点距离很近，脉动风压相关性可能很小。

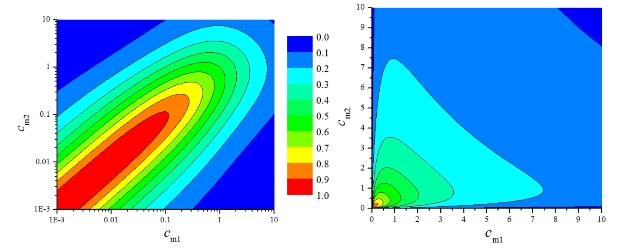
图5-5　相关系数随两点相关参数cm1、cm2的变化等值线图

当滤波相干系数c12→∞时，无论ωm1/ωm2取值如何，都有即完全无关。说明在相干指数很大kc→∞，或两点相距较远D12→∞，或风速很小U→0时，都可能存在脉动风压相关性很小的可能。

当滤波相干系数0＜c12＜∞时，定义无量纲数cmi=c12ωmi（i=1，2）为i点的相关参数，则式（5-18）亦可表达为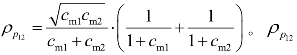随cm1、cm2的变化等值线图见图5-5。特别地，当两点脉动风压自功率谱的峰值频率相等，即ωm1=ωm2=ωm时，即cm1=cm2=cm，有

这里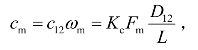，由此可以看出，滤波型相干指数Kc与无量纲峰值频率Fm的乘积是评价风荷载相关性的重要参数，也是预估背景效应的关键参数之一。

将式（5-19）的形式代入式（5-16），得到背景效应系数μc与风压谱参数的关系式，

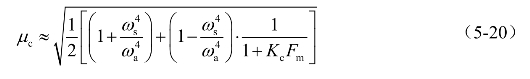
该式可作为预估背景效应的概念表达式。然而，随着自由度增加背景效应系数μc的取值出现一些离散性，与多自由度结构风荷载相关性的复杂程度有关，但其概念性趋势不发生本质改变。针对实际大跨度屋盖多自由度结构的背景效应系数μc的结果，将在第6章的参数分析中进行展开。