本节分别采用传统的时程分析法、传统的频域分析法[式(2-62)]以及本章提出的风振响应算法对上述三个模型进行风振响应计算,对比几种算法的精度以及效率。计算环境为采用Intel Core i7-4790 CPU @ 3.60 GHz,16.0 GB RAM,Windows 7 64位操作系统,MATLAB 2012b软件平台。
其中,悬挑桁架的计算结果如图4-12及表4-2所示。可以发现,本文算法的精度可以达到与传统方法相一致的级别,由于模态耦合效应的存在,在计算时并非考虑越多模态,计算结果越大,模态位移之间存在着负相关的可能。因此,考虑2阶CQC时计算结果小于仅考虑1阶模态。此外,在这个工况还计算了考虑所有模态的计算结果,计算结果与考虑截断频率以内的2阶计算结果近乎一致,说明在这种情况下,截断频率满足计算的要求,并不用考虑高频的补偿。在计算效率上也可以看出,采用本文算法计算时间可大幅度缩短,利于参数化分析的开展。
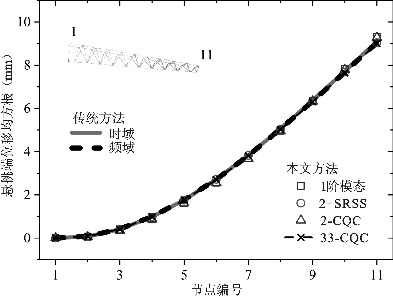
图4-12 悬挑桁架模型位移响应均方根结果
表4-2 悬挑桁架模型计算结果及计算效率

悬挑网架的计算结果如图4-13和表4-3所示。其中,表中的精度指标定义为,与传统时域方法相比,屋盖所有节点位移响应均方根的相对误差平均值与最大值。可以看出,即便是形式较为简单的悬挑屋盖,不考虑频率耦合效应时,即使考虑高阶频率的影响,结果还是会产生较大偏差。合理地考虑频率耦合效应会使计算误差大为降低,如本算例中仅考虑前3阶耦合模态,精度大为提高,相比于考虑全部20阶耦合模态计算效率也大为提高。

图4-13 悬挑网架模型位移响应均方根结果
表4-3 悬挑网架模型计算精度及效率指标

图4-14给出了各阶模态的模态响应均方根及耦合模态的模态响应协方差。可以看出,悬挑网架的风致振动以前3阶模态贡献为主,1、2阶模态的耦合效应较为明显,贡献量为正;1、3阶模态的耦合效应贡献量为负。由图4-11b的模态形状可以看出,1、2阶模态的耦合效应使得位移响应均方根呈现出非对称的形式。

图4-14 悬挑网架模型模态响应计算结果
单层球面网壳计算结果如图4-15及表4-4所示。其中,用最大位移响应均方根相对传统时域方法计算结果的误差作为精度指标。在本算例中,高阶SSRS法显然不能满足计算精度要求,耦合模态阶数选取为20阶仍有较大误差,选取耦合模态阶数到50阶时,计算精度能够满足要求。

图4-15 单层球面网壳模型位移响应均方根结果
表4-4 单层球面网壳模型计算精度及效率指标(https://www.xing528.com)

图4-16a给出了单层球面网壳各阶自振频率及模态响应均方根值。由图可以发现,单层球面网壳自振频率频率密集,且在某一阶频率后存在“突变”,其阶数与节点数相接近,该阶后的模态响应均方根远远小于前面阶数响应的值。因此,原则上这类屋盖计算时选取的模态组合阶数不应小于其节点数。此外,图中还给出了对风振贡献较大的第1、2、170阶模态的形状,可以看出贡献较大的模态分别表现为结构的整体横向(第1阶)、侧向(第2阶)和竖向(第170阶)振动。图4-16b给出了贡献最为突出的20阶耦合模态,由图可以看出,单层球面网壳的耦合模态既存在正贡献量,也存在负贡献量,与其他两个算例相比更为复杂。

图4-16 单层球面网壳模态响应计算结果
通过对比可以发现,单层球面网壳需要考虑更多阶的耦合模态,耦合模态阶数的合理选择直接关系到计算的精度和效率。因此,有必要结合算例讨论耦合模态计算阶数N1选取的问题。为量化耦合模态计算阶数N1对计算精度和效率的影响,定义如下三个参数。
1)模态累积贡献率Λ,定义为前N1阶最大模态响应均方根与全部N0阶模态响应均方根之和的比,如式(4-53)所示。

2)模态耦合相对误差Ξ,定义为以N0-CQC为基准,最大位移响应均方根为指标,N1/N0-CQC组合方法的计算结果的相对误差,如式(4-54)所示。

3)计算时长比Γ,定义为N1/N0-CQC与N0-CQC计算时长的比值,如式(4-55)所示。

在不同耦合模态计算阶数N1取值的情况下,统计上述悬挑网架和单层球面网壳算例的上述三个参数,如图4-17所示。由图可以发现,悬挑网架模态累计贡献率增长迅速,仅第2阶就可以到达90%以上,模态耦合相对误差随之迅速下降。而单层球面网壳模态累计贡献率增长趋势较为缓慢,相对应地,其模态耦合相对误差曲线的下降趋势呈现阶梯状。计算时长比随阶数呈二次曲线增长,起始点的值与计算准备工作占总时长的比有关,结构频率越稀疏,计算的模态阶数越少,则计算总时长越短,使得起始点值越大。
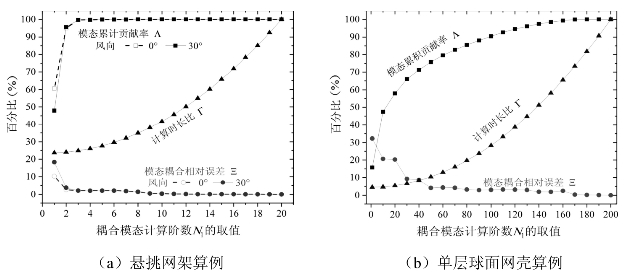
图4-17 耦合模态计算阶数N1对计算精度和效率的影响
为进一步探讨耦合模态计算阶数N1的选取原则,以模态累积贡献率Λ为横坐标,其他两个参数Ξ、Γ为纵坐标,将算例结果绘制在图4-18中。经过统计发现,模态耦合相对误差Ξ随模态累积贡献率Λ下降的斜率接近0.4。在保证计算精度的前提下尽可能提高计算效率,建议选取耦合模态计算阶数N1时,应保证模态累积贡献率Λ超过70%,这样一般可将模态耦合相对误差Ξ控制在10%以内,计算时长大约是完整计算的30%。

图4-18 耦合模态计算阶数N1的选取原则
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




