简化模态组合方法-基于风压谱的大跨度屋盖主体结构抗风设计理论

从2.4.2节中可以看出，4.2.2节基于滤波求解的频域积分是根据模态分解法推导出来的。模态分解法虽然提供了一种解耦的思想，使得风振响应可以在各个模态分量上求解，合适地选择模态能够使计算得到简化，但是针对复杂结构，忽略某些高阶模态或忽略模态耦合的影响可能产生较大的计算误差。

一般地，在结构模态（自振）分析中，结构模态的总数等于自由度数ND。实际结构自由度数成千上万，在计算中考虑所有模态是不现实且不必要的。即便是时域分析，也受到采样频率的限制，不能考虑所有模态的影响。因此在计算中，模态阶数限定在足够大的前N0阶。

根据4.2节计算的频域积分，可以求根据式（2-74）出各阶模态响应协方差，将式（2-72）展开，取前N0阶模态，

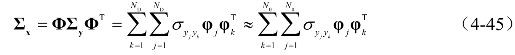
对式（4-45）主对角线元素取平方根可得，各自由度上的风振位移均方根σxi（i=1，2，…，ND）

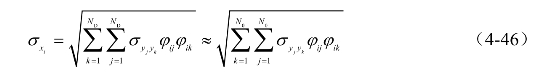
式中，φij、φik分别表示第j、k阶模态上第i自由度的位移分量，为模态矩阵Φ中相应位置的元素。

同样地，对风振响应（内力，支反力等），式（4-45）、式（4-46）变为

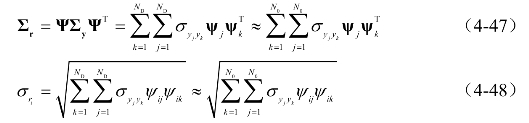
式中，ψij、ψik分别表示第j、k阶模态上第i个响应的分量，为模态响应矩阵Ψ中相应位置的元素。

由式（4-46）、式（4-48）可见，各阶模态对响应的贡献系数主要体现在模态响应协方差中，若仅取模态响应协方差矩阵Σy主对角元素（即j=k的情况），可得

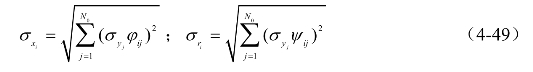
式中，为第j阶模态响应均方根（j=1，2，…，ND）。结构动力响应表示为各阶模态分量上的响应平方和开根号的形式，顾名思义，这种模态组合方法称为平方和开根号（square root of the sum of the squares，SRSS）法，忽略了模态响应的协方差及耦合模态的影响。像式（4-46）、式（4-48）中那样的模态组合方法，称为完全二次项组合（complete quadratic combination，CQC）法。

传统观点认为，当结构自振频率较为稀疏（各阶自振频率间隔较大）时，模态组合时可忽略耦合效应采用SRSS法，否则需采用CQC法考虑模态耦合效应。实际上，模态耦合效应还与模态间的相关性（正交性）有关，后文将结合具体算例详细探讨该说法的适用性，但针对大跨度屋盖结构，模态耦合效应明显目前已得到多方面的论证。因而，如何简化考虑模态耦合效应成为该类结构风振计算的关键。

本节考虑通过对模态响应协方差矩阵Σy中的非主要元素进行忽略，实现对CQC法的简化。具体思路如下，如图4-6为模态响应协方差矩阵Σy示意图。理论上，Σy矩阵的阶数为自由度数ND，取前N0阶进行计算，相当于将N0×N0以外的元素置为0。进一步计算N0阶主对角元素（图中用“×”符号表示）后，仅取最大的N1阶（图中用“⊗”符号表示）进行非主对角元素的计算（图中用“*”符号表示），其余的元素（图中用“·”符号表示）置为0。这样相当于忽略了贡献量本身比较小的模态间的耦合效应，由于各阶模态响应的相关系数不会超过1，因而对于模态响应本身较小的模态阶数，耦合作用相对也比较微弱，可以忽略不计。综上所述，将模态组合的各种方式总结如下。

（1）完全CQC法

需要对ND×ND的Σy矩阵进行求解，最为精确，但计算代价最大。

（2）N0-CQC法(https://www.xing528.com)

对Σy矩阵的前N0阶进行计算，较为精确，计算代价较大。

（3）N1/N0-CQC法

属于简化的CQC法，忽略示意图4-6中的“·”符号代表的元素，较为精确，计算量较小。

（4）N0-SRSS法

仅对Σy矩阵的前N0阶主对角元素进行计算，针对复杂结构精度较差，计算代价很小。

（5）一阶振型法

仅对Σy矩阵的左上角第一个元素进行计算，仅适用于非常简化的结构，计算代价最小，仅用于对结构动力响应的预估。

图4-6　简化CQC法与模态响应矩阵Σy示意图

若将该算法的计算量定义为计算频域积分σabjk的次数，则以上几种模态组合的计算量见表4-1。由表可知，计算量主要和自由度数ND、加载节点数NL、计算选取的模态阶数N0和考虑耦合模态阶数N1有关。一般地，加载点节点数NL和自由度数呈正比，即NL∝ND；计算选取的模态阶数N0理论上应与自由度数成正比，但当自由度数较大时，所选取的模态阶数可为某一定值，即N0∝ND0～1；考虑耦合模态的阶数N1与模态贡献特征等因素有关，总体来说与N0类似，有N0∝ND0～1。因此，算法的时间复杂度是自由度数的平方到四次方，也就是说，随着自由度数的增加，结构风振响应计算时间呈平方到四次方的量级增长。

表4-1　几种模态组合方法的计算量

图4-7给出了一般情况下，计算量随自由度数增长的曲线，当结构自由度数增大到一定程度，所选取计算的模态阶数不再增长时，计算的时间复杂度均变为平方，合理地选取耦合模态的计算阶数能够大大降低计算量。图4-8给出了某计算工况，加载节点总数NL=100，选取计算模态阶数N0=200，变化不同耦合模态计算阶数N1时的计算量与计算时长的曲线。其中计算时长是在4.2.2节的计算环境运行的统计结果，与4.2.2节中介绍的运行结果较为接近。在简化的N1/N0-CQC法中，计算量和计算时长随着N1的增长呈平方增长趋势。N1的具体取值方法将在4.4节中结合算例分析进行讨论。

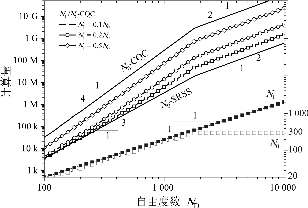
图4-7　计算量随自由度数ND增长的曲线

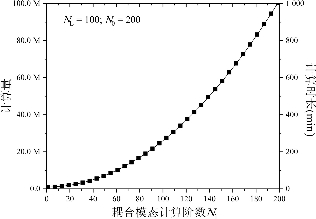
4-8　N1/N0-CQC法中计算量和计算时长随N1增长的曲线