大跨度屋盖主体结构抗风设计理论中的单自由度体系模型

将自功率谱的滤波表示式（4-1）代入式（2-59）中，有

积分项中的被积函数可以写成形如式（3-1）的滤波形式，即分子多项式为常数，滤波多项式K(ϖ)=V-1(ϖ)·Δ(ϖ)。

当自功率谱的滤波形式取式（4-2）时，滤波多项式次数为m=4次，分母多项式为8次，分子多项式为0次。这里仅给出行列式法的求解过程。

首先，可滤波多项式为

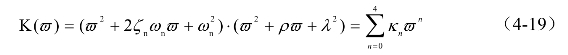
将该多项式展开，得

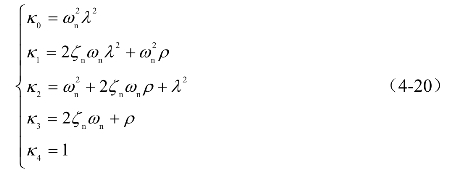
令θ0=1，θ1=θ2=θ3=0；代入式（2-52）至式（2-54），化简后，得

当自功率谱的滤波形式取式（4-8）时，进行类似的计算，可得，

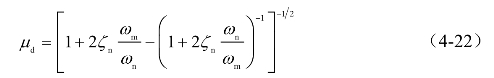
阻尼比ζn=0.02时，按式（4-21）、式（4-22）计算的动力系数μd随频率比ωn/ωm的变化曲线如图4-4所示。由图可知，式（4-22）的计算结果即为式（4-21）取λ0→∞的极限，读者可自行验证。当λ0足够大（λ0＞5）时，可用式（4-22）计算动力系数μd。

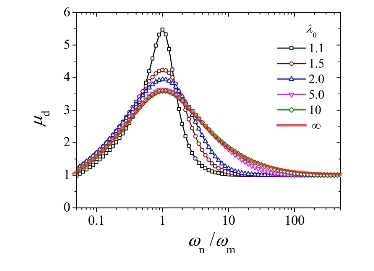
图4-4　动力系数μd随频率比ωn/ωm的变化曲线

单自由度结构动力系数μd的解析计算有助于对简单结构风振响应的预估，尤其是在结构初步设计时，该公式可用于初步确定结构的等效静风荷载。后面章节还将根据此公式给出一种结构的等效静风荷载表达形式。(www.xing528.com)

除此之外，针对于可简化为单自由度体系的线性结构，如高层高耸结构，在简化分析时，还可以类比式（2-58）、式（2-59）定义的单自由度体系位移响应均方根和位移动力响应系数，定义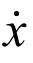速度、加速度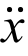响应均方根（和）及其动力效应系数（μv和μa）的解析表达式如下所示。

可以发现，速度响应均方根位移响应谱的2阶谱矩，加速度响应均方根为位移响应谱的4阶谱矩，则根据式（2-49）、式（2-50）可计算位移响应的2阶规律系数αx2和带宽系数εx2。

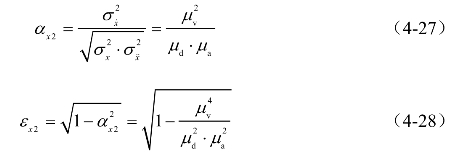
上述式（4-23）至式（4-28）均可由滤波积分得到解析表达式，其过程可由读者自行推导，结果经整理可表达为如下的简洁形式，

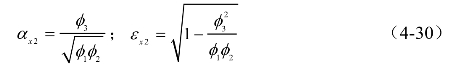
其中，φ1、φ2、φ3为频率比、阻尼比和频谱带宽相关的参数，当滤波形式采用式（4-8）时为，

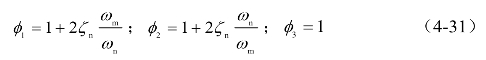
当滤波形式采用式（4-2）时为，

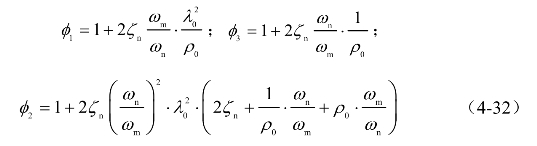
其中μd的计算结果与上文式（4-21）至式（4-22）结果一致，读者可自行验证。图4-5给出了阻尼比ζn=0.02时μv、μa、αx2和εx2的计算结果。

值得说明的是，上述解析解可应用于预估单自由度结构的振动响应及疲劳效应，尤其是单自由度为主的高层或高耸结构，利用测力天平得到的荷载谱采用4.1节的滤波表示法得到频谱参数，可通过式（4-29）至式（4-32）预估结构的位移、加速度响应及振动响应带宽系数。

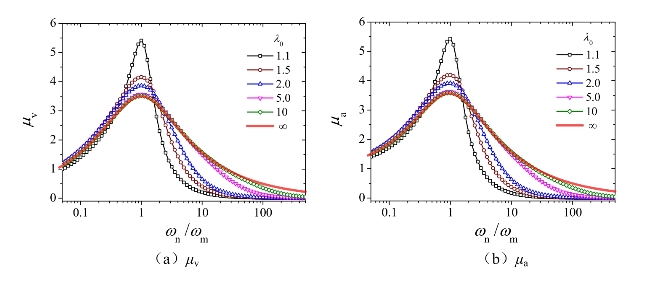
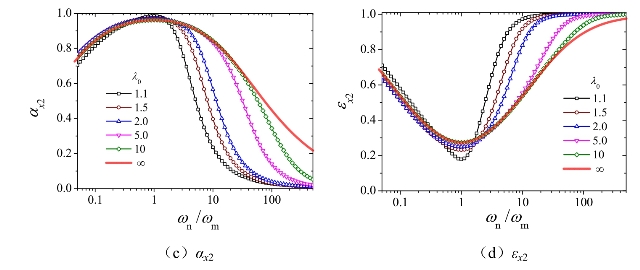
图4-5　单自由度体系响应参数μv、μa、αx2和εx2随频率比ωn/ωm的变化曲线