【摘要】:图4-3指数型和有理型相干函数模型4.1.2.2互功率谱的滤波表示将自功率谱[式(4-1)、相干函数式(4-9)]的滤波表示代入式,进行分母有理化并取实部,可以得到互功率谱的滤波表示,式中,分子多项式为滤波多项式Δabc()=Δa()·Δb ()·Δc()。
4.1.2.1 相干函数的滤波表示
由相干函数的定义式(2-32)可知,互功率谱可由自功率谱和相干函数来表示,4.1.1节给出了自功率谱的滤波形式,若要将互功率谱进行滤波表示,相干函数的形式至关重要。第3章中给出了采用相干函数的指数函数,如式(3-26)所示,本节试图将其用有理函数进行近似,该过程称为相干函数的滤波表示。
考虑采用式(4-9)右边的有理函数模型对指数型相干函数进行近似,
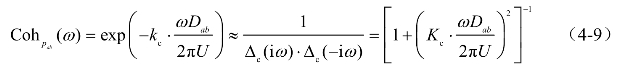
式中,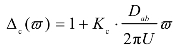 为相干函数的滤波多项式,Kc为滤波型相干指数。相干函数的滤波表示还需建立相干指数kc与滤波型相干指数Kc的联系。
为相干函数的滤波多项式,Kc为滤波型相干指数。相干函数的滤波表示还需建立相干指数kc与滤波型相干指数Kc的联系。
由于结构风振响应计算需要进行频域积分,所以类似地假设式(4-9)约等号两侧的频域积分相等,即
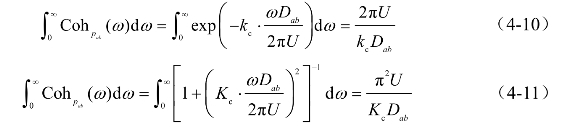
根据式(4-10)和式(4-11),可得,![]() 因此,相干函数的滤波表示可写成,
因此,相干函数的滤波表示可写成,
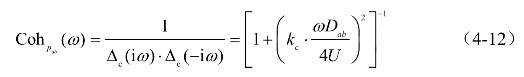
后文为简化表述,令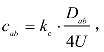 相干函数的滤波多项式为Δc(ϖ)=1+cabϖ。(https://www.xing528.com)
相干函数的滤波多项式为Δc(ϖ)=1+cabϖ。(https://www.xing528.com)
图4-3给出了指数型相干函数与有理型相干函数的曲线,可以发现,有理函数也能够近似地反映相干函数的衰减趋势。工程上,将相干函数用有理函数近似表示是合理的,在风振计算中的有效性将在本章后文给出的算例分析中进行验证。
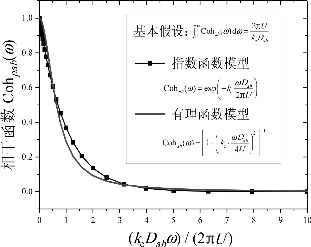
图4-3 指数型和有理型相干函数模型
4.1.2.2 互功率谱的滤波表示
将自功率谱[式(4-1)、相干函数式(4-9)]的滤波表示代入式(2-32),进行分母有理化并取实部,可以得到互功率谱的滤波表示,
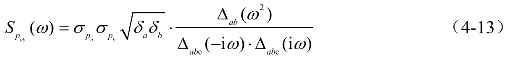
式中,分子多项式为![]() 滤波多项式Δabc(ϖ)=Δa(ϖ)·Δb (ϖ)·Δc(ϖ)。当代入式(4-2)时,有
滤波多项式Δabc(ϖ)=Δa(ϖ)·Δb (ϖ)·Δc(ϖ)。当代入式(4-2)时,有
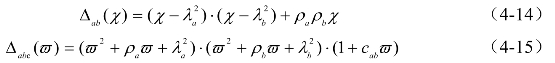
当代入式(4-8)时,有
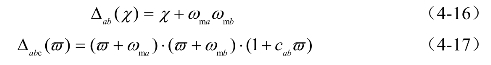
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




