上节中的三参数功率谱模型虽然能够较为灵活、准确地表示各种形状的自功率谱,但根据参数κ、Sm确定中间参数α的过程需要对式(3-16)表示的非线性积分方程进行求解,不便于工程人员掌握。因此,有必要对三参数模型进一步简化。基于3.2.2.2节的统计分析,发现参数κ、Sm在统计上集中于(1,0.3),本节将围绕该结果进行深入探讨,最终得到自功率谱的工程模型。
3.2.3.1 模型的提出
根据维纳-辛钦关系,若将风压的自相关函数表示为指数型函数,

其中,衰减指数取峰值频率ωm。则自功率谱函数表示为,
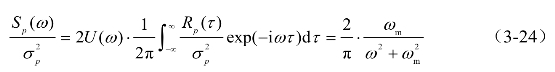
将式(3-24)表示为无量纲的形式,

式(3-25)表示的自功率谱模型,对应于三参数模型中取κ=1,Sm=1/π≈0.3,α=2的特殊解。该式恰好满足κ、Sm的统计趋势,也从一个侧面说明自相关函数满足指数型函数的假设是合理的。

图3-12 自相关函数及自功率谱曲线及其工程模型
图3-12给出了所有工况下自相关函数及自功率谱的无量纲曲线,由图可以发现,虽然曲线在数值上具有一定的离散性,整体趋势与上述模型一致。因此可以认为,采用上述模型对三参数自功率谱模型进行工程简化是合理的,称式(3-23)为自相关函数的工程模型,式(3-25)为自功率谱的工程模型。可见,在自功率谱的工程模型中,仅保留了一个参数,即峰值频率参数Fm(或fm、ωm)。下面对该参数的意义及取值进行详细分析讨论。
3.2.3.2 峰值频率fm分析
峰值频率参数是三参数模型中最重要的参数,完全独立于风压自功率谱曲线的形状,作为风压自功率谱工程模型中的唯一参数,对描述脉动风荷载频域特性有着重要意义。而且,峰值频率是三参数模型中唯一与有量纲频率相关的参数,在结构响应分析时,还可能与结构自振频率结合起来,因而在预估风振效应方面也具有一定的工程价值。根据前文的分析,将峰值频率的意义总结为如下几方面。
(1)峰值频率是无量纲自功率谱峰值对应的频率
根据风荷载主要作用于低频的特性,从风压自功率谱中难以定义风荷载的主导频率(或卓越频率),但在无量纲功率谱中,功率谱上乘以频率项表征了在单位时间内脉动风压的总功率在不同频率上的分布,此时曲线具有峰值。对应的峰值频率即单位时间内脉动能量最大的频率成分。从这个角度上,峰值频率可认为是脉动风荷载的卓越频率。
(2)峰值圆频率是脉动风压自相关函数的衰减指数
当采用自功率谱的工程模型时,假设脉动风压自相关函数随时差τ呈指数型衰减,此时,衰减指数恰好为峰值圆频率。这也说明峰值频率参数与风压自相关性的衰减联系紧密,是特征湍流作用的重要特征参数。
(3)无量纲峰值频率可视为建筑尺度与特征湍流流场特征尺度的比值
根据Taylor冻结假设[158],根据量纲分析法定义特征湍流流场特征尺度Lt=U/fm,则无量纲频率为Fm=fm/U=L/Lt。在一定风速下,当峰值频率较大时,说明该局部作用的特征湍流流场特征尺度较小,在建筑物的迎风分离区(尤其是锥状涡)和尾流漩涡脱落处较为常见,因为这些部位的特征湍流主要以小尺度漩涡主导;当峰值频率较小时,说明该局部作用的特征湍流流场特征尺度较大,尤其在曲面屋盖的顶部气流加速区表现得尤为明显。由此可见,峰值频率可以作为描述特征湍流特性的参数。
峰值频率作为风荷载的特征频率,可以与结构自振频率结合起来,形成荷载-结构频率比的概念,预估结构在风荷载作用下的动力效应。第4、5章也将针对这方面展开。(https://www.xing528.com)
图3-13至图3-15给出了无量纲峰值频率Fm在各类屋盖典型工况的分布等值线图。按照3.2.1节对屋盖的分类,分别对三类屋盖形式进行分析。
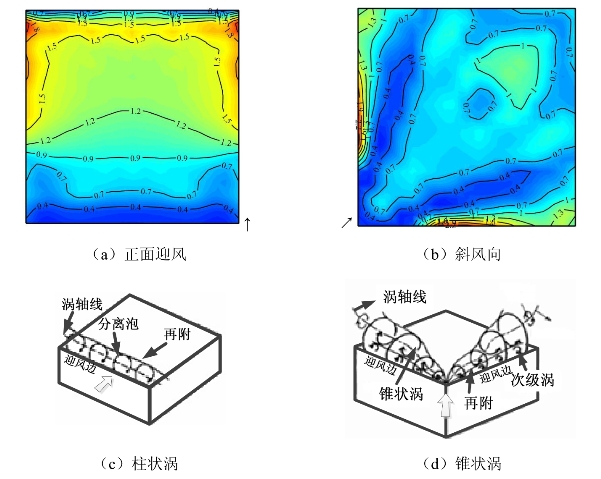
图3-13 平屋盖(L=B,H/L=1/4)Fm等值线图及流场示意图
第Ⅰ类带有尖角钝体特性的平屋盖和鞍形屋盖典型工况的Fm等值线图分别见图3-13和图3-14。由图3-13可知,平屋盖在正面迎风时,气流在迎风边分离,屋盖前缘形成“分离泡”漩涡尺度相对较大,分离区内的风压峰值频率较低;随着气流在屋盖中后部的再附,分离泡破裂产生小尺度的湍流,峰值频率随之增高,屋盖尾部气流重新组织并伴随着漩涡脱落,峰值频率略有降低。此外,屋盖两侧受横向分离剪切流的影响,气流与屋盖侧风边缘碰撞产生小尺度不规则的漩涡,因此屋盖两端峰值频率较大,呈现出端部效应。在斜向风作用下,气流在屋盖两个迎风边分离形成锥状涡,在气流分离的前缘存在尺度很小的次级涡,峰值频率很高;在锥状涡轴线作用位置处漩涡尺度较大,峰值频率较低;随着漩涡在屋盖中部及尾部的再附与脱落,湍流尺度变小,峰值频率略有升高。鞍形屋盖上的特征湍流主要表现为锥状涡[76-78,217],但相比于平屋盖,鞍形屋盖还受到曲率的影响,情况更为复杂。如图3-14所示,对于封闭屋盖,在高点迎风时,气流绕过高点形成锥状涡,但其作用范围较小,在两侧迎风边中后部形成高频的小尺度漩涡在屋盖尾部脱落;低点迎风时,与平屋盖不同的是,在迎风边缘没有形成小尺度的次级涡,迎风边的气流随着屋盖边缘爬升,湍流尺度较大,峰值频率略低于锥状涡轴线处的频率。由于屋盖存在一定曲率,漩涡再附后气流过渡较为平缓,再附区峰值频率较低,气流在屋盖尾部脱落时,峰值频率略有升高,与曲面屋盖的规律是相近的。开敞屋盖的规律类似,但受到屋盖下部气流的影响,净风压的峰值频率总体略有提高,高频作用的区域向屋盖两侧风向角点偏移。

图3-14 鞍形屋盖(H1/L=1/8,r/B=1/5)Fm等值线图
第Ⅱ类具有平板流特性的悬挑屋盖典型工况的Fm等值线图如图3-15所示,由图可以发现,看台开敞情况下峰值频率整体高于看台封闭情况下,与上文的封闭与开敞鞍形屋盖的结论是类似的,原因是下部的开敞通风促进了屋盖下部气流的分离和漩涡脱落,与屋盖上表面共同作用引起。此外,还可以发现屋盖表面脉动风压端部效应明显,这是由屋盖边缘处的局部锥涡所致,针对矩形平面屋盖,这种作用来源于来流中的横向湍流作用;而针对弧形平面屋盖,来源于其迎风角点与来流存在一定的夹角,这种局部湍流作用范围可延伸到屋盖两侧的1/4~1/3处,而屋盖中部主要是二维特性明显的柱状涡作用,整体峰值频率略高于边跨位置。

图3-15 悬挑屋盖(L/B=1/3,H=L,θ=5°)Fm等值线图及流场示意图
第Ⅲ类是以柱面和球面屋盖为代表的曲面屋盖,典型工况的Fm等值线图如图3-16所示。由图可以发现,在前缘迎风区形成正压,此时的风压谱与来流风谱相接近;当气流经过屋盖顶部时,气流加速,产生较大负压,风压峰值频率急剧下降,说明该区域特征湍流尺度较大;气流达到分离点后从屋盖表面脱落,形成较高频率的小尺度特征湍流。对于柱面屋盖,从屋盖中后部开始,端部效应较为明显,主要是分离剪切流的作用;而对于球面屋盖,风压谱峰值频率的二维特性保持较好。此外,还可以发现迎风区和尾流区的投影面积随着矢跨比的减小而减小,但在柱面和球面屋盖上相应区域的峰值频率取值基本一致,且随矢跨比变化较小。
图3-17给出了缩尺风洞试验所有工况的峰值频率转化到原型的结果统计图,由图可知,大跨度屋盖风压谱峰值频率大多分布在1 Hz以内,曲面屋盖(第Ⅲ类)峰值频率总体小于尖角屋盖(第Ⅰ类)和悬挑屋盖(第Ⅱ类),悬挑屋盖(第Ⅱ类)峰值频率分布范围较尖角屋盖(第Ⅰ类)更广。曲面屋盖(第Ⅲ类)主导峰值频率集中在0.1 Hz以下,尖角屋盖(第Ⅰ类)和悬挑屋盖(第Ⅱ类)主导峰值频率集中在0.1~0.2 Hz。经统计分析,99%的峰值频率在0.78 Hz以下,95%的峰值频率在0.42 Hz以下,75%的峰值频率在0.20 Hz以下,50%的峰值频率在0.13 Hz以下。一般的实际大跨度屋盖结构一阶自振频率大于0.8 Hz,说明结构频率总是大于或者说是远大于风荷载的峰值频率。
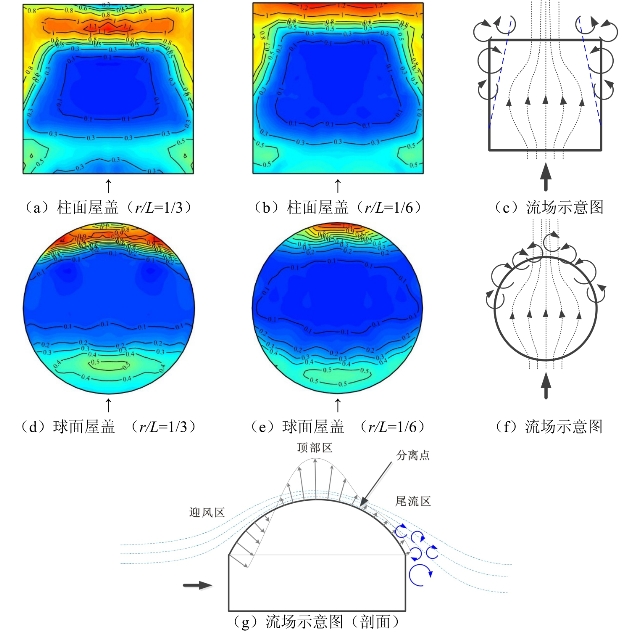
图3-16 柱面及球面屋盖(h/L=1/2)Fm等值线图及流场示意图
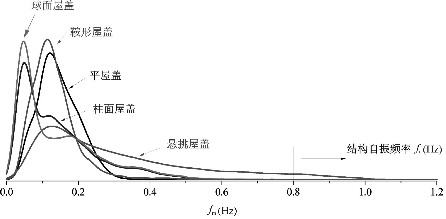
图3-17 全部工况下原型峰值频率fm统计分布图
为方便工程应用,经过参数的统计整理,将相近的参数取值进行合并;对邻近风向角的数据进行了包络,给出无量纲峰值频率的分区值作为简化计算的依据,如表3-3所示,分区示意图如图3-18所示。图中,特征尺寸z0取值参考美国规范ASCE 7-16[110],为屋盖水平尺寸的10%、屋盖平均高度的40%中二者取小值,同时不小于最小水平尺寸的4%或1 m。在条件允许情况下,建议采用峰值频率实验结果进行精细化的设计分析。
表3-3 不同类型屋盖Fm分区建议值


图3-18 屋盖分区示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




