基于风压谱的大跨度屋盖主体结构抗风设计成果

3.2.2.1　模型的提出

借鉴第2章中风速谱模型式（2-8），将无量纲谱表达为如下形式：

式中，为无量纲风荷载谱，Sp(f)为单边风荷载谱（Pa2·s），f为频率为脉动风荷载总能量（方差Pa2），为无量纲频率，f0是参考频率（Hz）。通常U为特征风速（m/s），如来流某一高度处的平均风速或脉动风速均方根等，L为特征尺度（m）如建筑物高度、宽度、参考点高度或湍流积分尺度等。

A、B、C、α、β、γ为式（3-1）的谱模型参数，后文称为原始谱模型参数。由于原始谱模型参数是由大气边界层风速谱类比而得到的，参数的分析可参见文献[168]。值得强调的是，六个原始谱模型参数对于式（3-1）是存在冗余的，归结为两点：①式（3-1）分数线上下可约分，一般的处理方式是不妨取C=1，本文也采用同样的做法；②能量的归一化准则式（3-2）为原始谱模型参数提供了一个约束条件。因此，六个原始谱模型参数是相互制约的，最终可缩减为四个自由参数。

式中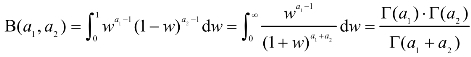，为Beta函数；为Gamma函数，Re[ai]＞0，i=1，2。

在3.2.1节的基础上，将无量纲自功率谱曲线S-F用单峰函数的形式进行简化描述。为观察自功率谱函数的数学特征便于自功率谱建模，将无量纲自功率谱曲线S-F绘制在双对数坐标轴下，如图3-6所示。曲线在低频段上升和高频段衰减可以近似看作直线，低频段上升斜率一般为k1，高频段的衰减下降段斜率绝对值定义为k2谱曲线峰值对应的频率fm（Hz，转化为无量纲频率表示为Fm=fm/f0）及峰值Sm四个参数。由曲线的几何特征可知，上述四个参数是独立的。由代数学理论可知，上述四个参数理论上可由六个原始谱模型参数表示，后文将推导其间的关系式（缩减关系），进而得到本文的风压谱模型。称参数k1，k2，fm（或Fm）及Sm为缩减谱模型参数，简称为谱模型参数。

图3-6　风压自功率谱模型示意图

式（3-1）两边取对数，转化为对数坐标：

求导，得：

得到双对数坐标下的导数：

双对数坐标下的低频段斜率k1、高频段斜率k2分别为

得到无量纲谱峰值Sm及其对应的无量纲频率Fm=fm/f0。

式（3-6）、式（3-7）、式（3-9）、式（3-10）为原始谱模型参数到谱模型参数的缩减关系。将上述表达式带入式（3-1）整理可得，

其中，F′为无量纲频率，α是由k1、k2、Sm根据方程（2-36）确定的中间参数，由能量归一化条件式（3-2）确定，表示为：

值得说明的是，式（3-12）为非线性积分方程，可有迭代法数值求解，迭代格式见式（3-13），后文将给出谱模型的求解结果。

由式（2-48）得，无量纲风压谱（3-11）的ν阶无量纲谱矩（-k1＜ν＜k2）表示为，

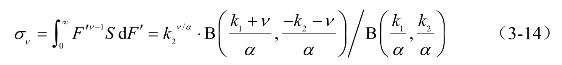
为考察缩减参数对谱曲线形状的影响，进行参数分析。由于无量纲峰值频率Fm仅影响谱曲线的峰值位置，不影响曲线形状，因此统一取为1.0。图3-7a、3-7c、3-7e给出了谱曲线随各缩减参数的变化，由图可知，三个缩减参数间耦合较小。原始谱模型参数随缩减参数k1、k2、Sm的变化见图3-7b、3-7d、3-7f，由图可知，随着k1的增大，参数A逐渐增大发散；随着k2的减小，参数A、B、α逐渐增大发散，参数β逐渐减小趋于零；随着Sm的增大，参数B逐渐增大发散，参数β逐渐减小趋于零；随着Sm的减小，参数B、β均逐渐增大发散。由此可见，第2章中表2-3中参数离散程度大主要是由于谱在某些特定的形状下，参数发生发散。(www.xing528.com)

图3-7　缩减参数对谱曲线的影响以及缩减关系曲线

由风洞试验数据统计发现，对于风压谱，一般有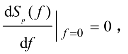因此，无量纲谱低频上升段斜率可取k1=1[218]。定义衰减指数κ=k2及功率谱曲线的峰值(Fm，Sm)，则风压自功率谱可由功率衰减指数κ、峰值功率Sm和峰值频率Fm三个参数表达，

其中，F′为无量纲频率，α是由κ、Sm，根据方程（3-16）确定的中间参数，

α与κ、Sm的取值关系求解结果见图3-8。

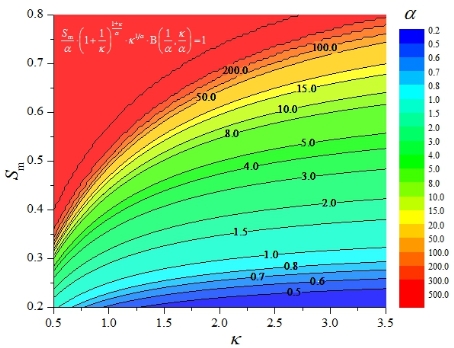
图3-8　中间参数α关于κ、Sm的等值线图

三参数模型中的Fm表示风荷载能量分布最大的无量纲频率，称为无量纲峰值频率，往往与特定的流场特征湍流现象相关。该参数对应的峰值频率为fm（Hz）或ωm（rad/s）。理论上，参数Sm的取值范围为(0，1)，取值越大，说明功率越集中于峰值频率；参数κ的取值范围为(0，∞)，取值越大，说明功率在高频范围衰减越快。此外，由式（3-16）还可以发现，无量纲峰值频率Fm与其他两参数κ、Sm的取值无关，从无量纲自功率谱曲线的几何特征上反映为Fm决定曲线的位置，κ、Sm决定曲线的形状。

将三参数自谱模型式（3-15）带入式（2-48），得到ν阶无量纲谱矩为

其中，阶数ν∈（1，κ）时，谱矩为有限值。谱矩也是后面章节基于滤波理论分析的重要参数，具体内容将在后续章节展开。

根据式（2-31）可得ν阶规律系数和带宽参数，如式（3-18）、式（3-19）所示。图3-9给出了描述谱带宽较为常用的1阶规律系数和带宽参数α1、ε1关于κ、Sm的等值线图。由参数的分布图可以看出，脉动风压自功率谱的带宽主要与衰减斜率κ有关。κ值越大，脉动风压的功率在高频区域衰减得越快，频谱越呈现窄带特性；反之，κ值越小，脉动功率在各频段的分布越趋于均匀，呈现出宽频特征。从定量角度来看，当κ＜2.0时，可以认为风压谱是宽带谱；当κ＞3.0时具有明显窄带特性，尤其是Sm＞0.5时。从后面统计分析中可以得出，湍流风场中的大跨度屋盖结构，绝大部分风压谱为宽带谱，极少存在窄带谱的情况。

图3-9　表示谱带宽的参数关于κ、Sm的等值线图

3.2.2.2　模型参数的识别与统计

自功率谱参数Sm、Fm、κ可根据S-F曲线，由式（3-20）至式（3-22）获得。

式中，为离散的无量纲频率，Nfft为傅里叶变换长度，为奈奎斯特（Nyquist）频率，为大于1的松弛因子，本文取1.5。

值得说明的是，三个自谱模型参数可以作为描述脉动风荷载频域特性的特征参数存入风荷载数据库中便于后续应用和分析。

综合分析不同屋盖上的自谱模型参数，得到各参数的取值规律。本节给出参数κ、Sm的边际分布及联合分布，如图3-10所示。由图中参数Sm的边际分布函数可知，参数Sm的取值很大程度上集中于0.3附近，经统计分析，95%的Sm在区间(0.24，0.54)内，中间50%的Sm在区间(0.28，0.37)内。而参数κ的分布集中程度虽然不如参数Sm，其众值发生在1附近，经统计分析，95%的κ在区间(0.6，2.4)内，中间50%的κ在区间(0.9，1.5)内。从κ、Sm的联合分布上可以看出，参数κ和Sm的分布存在较弱的正相关性。总体来看，散点主要集中于(1，0.3)附近，分别对应于每个参数的众值，为后文分析该数值的意义及自功率谱模型的工程简化奠定了基础。无量纲峰值频率Fm的取值规律分析将在3.2.3节中展开。

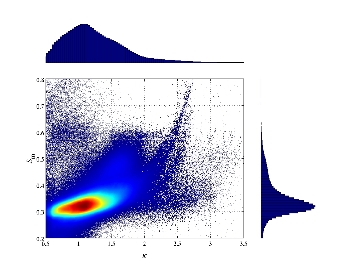
图3-10　谱模型参数κ、Sm的联合分布及边际分布

3.2.2.3　模型的对比验证

为验证模型的有效性，本文还选取了相关文献中的典型屋盖测点风压谱数据及模型进行比较，如图3-11所示，其中包含现场实测数据[219，220]及风洞实验数据[27，221，42，44，51]。Kumar和Stathopoulos[221]采用两个指数函数线性组合的方式建立平屋盖的风压谱模型，以模拟平屋盖无量纲风压谱的双峰值情况。从图3-11a和图3-11b中可以看出，这种模型虽然能够体现功率谱的两个峰值，但在高频段迅速衰减，有可能低估风荷载高频处的脉动功率，很可能对风振响应分析造成不利影响。Uematsu等[27，42]分别拟合来流湍流和特征湍流的风压谱，将其线性组合来对屋盖任意一点的风压谱建模，如图3-11a所示。但采用这种建模方法需要对特征湍流的频谱特点进行准确合理的提取，对于流场较为复杂的情况（如锥状涡），模型的表达形式较为复杂烦琐。从图3-11中可以看出，本文的三参数模型能够较为灵活、准确地表示各种特征湍流作用下的自功率谱特性，且形式较为简洁。

图3-11　与文献中风压谱数据及模型的对比