风压场的随机模拟技术

随机信号的模拟主要基于蒙特卡洛（Monte-Carlo）方法，结合傅里叶变换及滤波方法模拟相应的脉动谱。对于高斯信号场的模拟，主要有谱表示法（spectral representation method，SRM）和线性滤波法。前者利用互谱密度矩阵分解逼近目标谱模型，后者则是将零均值的白噪声信号通过一系列线性滤波器得到相应的谱特征。

根据Shinizuka[202]和Deodatis[203]的理论，基于谱表示法的具有互功率谱密度矩阵Sx(ω)的随机高斯时程向量x(t)=[x1(t)，x2(t)，…，xn(t)]T表示为，

其中，Δω=2πfs/N为频率分辨率；Ljm(ω)为矩阵L(ω)中的元素，L(ω)为互功率谱密度矩阵Sx(ω)的Cholesky分解，即θjm(ω)为Ljm(ω)的辅角，即为[0，2π]均匀分布的随机相位。在此基础上，学者们提出引进快速傅里叶变换（fast fourior transform，FFT）和本征正交分解（POD）技术以加速模拟[204]。

针对非高斯风压场，非高斯过程y(t)一般通过转换函数y=g(x)映射为潜在高斯过程（Underlying Gaussian Process）x(t)。经过这种非线性映射，随机变量的统计矩（概率密度）、相关函数（频谱）发生了演变，需建立目标非高斯过程y(t)和潜在高斯过程x(t)的矩演变关系（2-88）和相关函数演变关系（2-89）以适应模拟目标的变化。

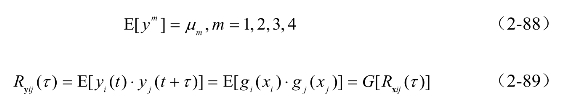
基于转换函数法的非高斯场模拟基本流程为，首先假定转换函数y=g(x)的形式，并根据目标统计矩由矩演变关系（2-88）确定转换函数中的参数（或采用概率密度演变关系拟合转换函数）。然后根据维纳-辛钦（Wiener-Khinchin）关系[177]，将目标互功率谱矩阵Sy(ω)进行逆傅里叶变换转化为互相关函数矩阵Ry(τ)，根据相关函数演变关系（2-89）确定潜在高斯过程的互相关函数矩阵Rx(τ)，进而得到潜在高斯过程的互功率谱矩阵Sx(ω)。最后根据谱表示法对得到潜在高斯过程后x(t)根据转化函数得到目标非高斯场y(t)，见图2-7。

图2-7　基于转换函数法的非高斯场模拟基本流程

下面给出基于三次多项式和双指数函数型转换函数的演变关系。

（1）三次多项式型转换函数[205]

(www.xing528.com)

矩演变关系为，

其相关函数演变关系为，

（2）双指数函数型转换函数[206]

其矩演变关系为，

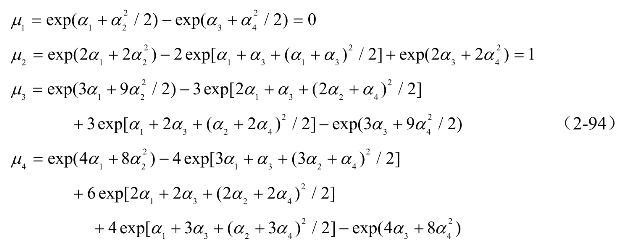
其相关函数演变关系为，

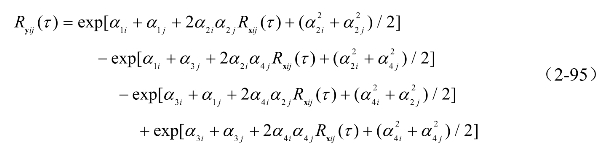
除此之外，转换函数一般多采用Hermite多项式展开[37，207]。陈新中等[81，208]提出了根据概率密度曲线（CDF）的转换函数估计方法。刘敏等[83，209—212]提出了分段Hermite函数（moment-based piecewise hermite polynomial model，PHPM）的转换函数估计方法，并改进了矩统计参数以适应强非高斯性。马兴亮等[213-214]提出了基于Johnson变换的方法，具体可参见相关文献。