自相关函数与自功率谱，基于风压谱的抗风设计理论

频谱（频谱密度）是指信号幅值、能量或功率在频域上的分布。脉动信号一般分为能量信号和功率信号。能量信号是指能量有限的信号，一般为脉冲式的信号；一般的随机信号多为功率信号，即能量无限但功率有限的信号，本文研究的风压和风振响应信号就属于这个范畴。因此，本文涉及的频谱一般指功率谱，也称为功率谱密度函数，是指信号的功率在频域上的分布。在数学上，一般用信号幅值的平方表征其能量。以脉动风压信号p(t)为例，根据巴塞瓦（Parseval）定理，其在时域上的平均功率定义为，

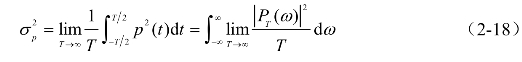
式中，为脉动风压p(t)在时段[-T/2，T/2]上的傅里叶（Fourier）变换，令则有，

其中，Gp(ω)和Sp(ω)分别为脉动风压p(t)的双边和单边自功率谱密度函数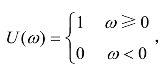，为单位阶跃函数。

由定义可知，功率谱的量纲为（信号量纲2/频率量纲），当采用频率f（Hz）代替圆频率ω（rad/s）时，由于ω=2πf，根据恒等变换条件，约定Sp(f)=2πSp(ω)。同样地，当采用无量纲频率F=f/f0=ω/ω0时，约定Sp(F)=ω0Sp(ω)=f0Sp(f)，保证了Sp(F)dF=Sp(ω)，dω=Sp(f)df。此外，在功率谱的表达上，还常采用归一化形式

和无量纲形式

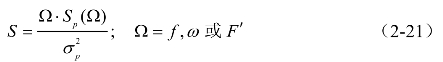
值得说明的是，在对数频率下有如下归一化形式，

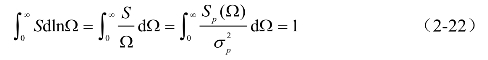
因此，无量纲功率谱通常在对数坐标下使用。除此之外，无量纲功率谱的形式中还包含信号的频率。在幅值相同的情况下，信号频率越高，单位时间内传递的能量越高。因此认为，无量纲功率谱更为综合地反映了信号在不同频率分量上的能量分布。还有文献称其为脉动信号的频率概率分布。(www.xing528.com)

根据维纳-辛钦（Wiener-Khinchin）定理[177]，对于宽平稳随机过程，其自功率谱密度函数与自相关函数构成一个傅里叶变换对，即

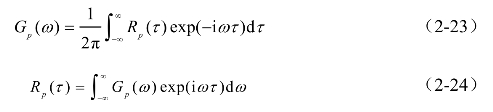
其中，自相关函数Rp(τ)定义为脉动风压时程p(t)在时差τ上的线性相关系数期望，即

维纳-辛钦定理建立了脉动信号在频域与时差域的联系，也提供了功率谱的一种估计方法。当时差为0时，有Rp(0)=σp2，称σp为脉动风压p(t)的均方根（root mean square，RMS）值，σp2为脉动风压p(t)的方差（variance），表征该信号的平均功率。

为简化表述，本节中的脉动风压符号及下标p，在后面章节中可由表示风压场中某点的脉动风压pa或pb替代。

常见的随机自然激励的归一化功率谱如图2-4所示，图中选取了典型的卡门风速（von-Karman）谱、描述地震动加速度的金井清（Kanai-Tajimi）谱、描述波浪运动的“北海联合海浪计划”（JONSWAP）谱。由图2-4可以看出，湍流风的作用较地震和海浪作用具有如下特征。

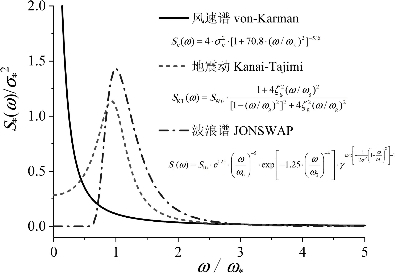
图2-4　常见的随机自然激励（风、地震、波浪）的归一化功率谱

（1）脉动功率在低频作用较为明显，表明风的作用是以大尺度涡旋为主，而高频的小尺度涡旋虽然比例有所下降，但会对结构产生一定的限幅抖振，这种作用在风振分析中尤为重要。

（2）没有明显的主导频率作用，或者说可能是主导频率被低频的脉动淹没，在归一化功率谱的高频没有明显的主导频率。显然，如果试图定义风荷载的特征频率，不能类比地震与波浪荷载的定义方式。因此，后文的分析中，由无量纲功率谱峰值定义风荷载的特征频率，并试图揭示该频率的数学及物理内涵。

（3）频谱表现出宽带特征，且带宽难于从谱曲线的几何上直观判断。目前可以确定的是，风荷载不完全是窄带信号，适用于窄带信号的分析理论在对风荷载进行分析时需要修正。后文也试图结合谱模型对风荷载的带宽特性进行说明。