主动土压力计算-土力学与地基基础

如图6-20所示，墙背与垂直线的夹角为α，填土表面倾角为β，墙高为H，填土与墙背之间的摩擦角为δ，土的内摩擦角为φ，土的凝聚力c＝0，假定滑动面BC通过墙踵，与水平方向的夹角为θ。

取滑动楔形体ABC作为隔离体进行受力分析，当滑动楔形体ABC向下滑动，处于极限平衡状态时，楔形体ABC上作用有以下三个力：

（1）滑动楔形体ABC自重W，当滑裂面的倾角θ确定后，由几何关系可计算土楔自重G=VABC×γ。

（2）滑动面BC上的反力R，该力是由于楔形体ABC滑动时产生的土粒之间的摩擦力在BC面上的合力，作用方向与BC面的法线的夹角等于土的内摩擦角φ。楔形体ABC下滑时，R的位置在法线的下侧。

（3）墙背AB对土楔体的反力E，其与主动土压力构成了作用力和方作用力，两者力的大小相等、作用线相互重合但方向相反。力E的作用线与墙背AB法线的夹角为δ（δ为土与墙之间的摩擦角）。楔形体ABC下滑时，力E的位置在法线的下侧。

楔形体ABC在以上三个力的作用下处于极限平衡状态，则由该三力构成的力的矢量三角形必然闭合。已知W的大小和方向，以及R、E的方向，可给出如图6-20（b）所示的力三角形。按正弦定理有

则

式中，ψ=90°-（δ+α）。

由公式（6-15）可知，滑动楔形体ABC自重W是θ的函数，φ和ψ为已知常数，因此E就是θ的单值函数，即E=f（θ），不同的θ对应着不同的P值。

主动土压力应为E=f（θ）的最大值，因此应令，用数值法求解θ后，再代入式（6-15），即可求得作用于墙背的主动土压力Ea。

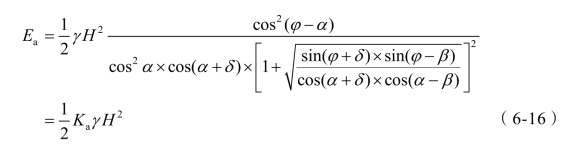
式中　γ——墙后填土的重度（kN/m3）；

　　　H——墙的高度（m）；

　　　Ka——库仑主动土压力系数，是φ、α、β、δ 的函数，见表6-3～表6-8；

　　　α——墙背倾角（墙背与铅直线的夹角），以铅直线为准，顺时针为负，称仰斜；逆时针为正，称俯斜；

　　　δ——墙背与填土之间的摩擦角，由试验确定；无试验资料时，一般取δ＝（1/3～2/3）φ，也可参考表6-9中的数值；

　　　φ——墙后填土的内摩擦角（°）；

　　　β——填土表面的倾角（°）。

当墙背直立（α＝0），墙面光滑（δ＝0），填土表面水平（β＝0）时，主动土压力系数为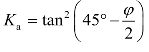，与朗肯主动土压力系数相同。式（6-16）变形为

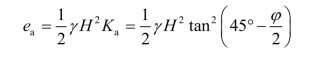
由此可知，朗肯主动土压力公式是库仑土压力公式的特殊情况。

沿墙高度分布的主动土压力强度ea，可通过对式（6-16）求导得出，即

由此可知，主动土压力强度沿墙高呈三角形分布，如图6-21所示。主动土压力合力作用点在离墙底的H/3高度处，作用线与墙背法线的夹角为δ，与水平面的夹角为δ＋α。

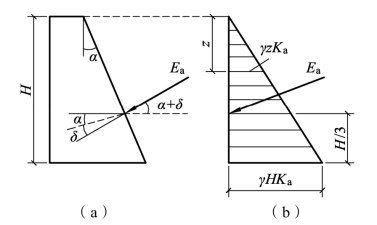
图6-21　主动土压力强度分布图

表6-3　主动土压力系数Ka值（δ＝0°）

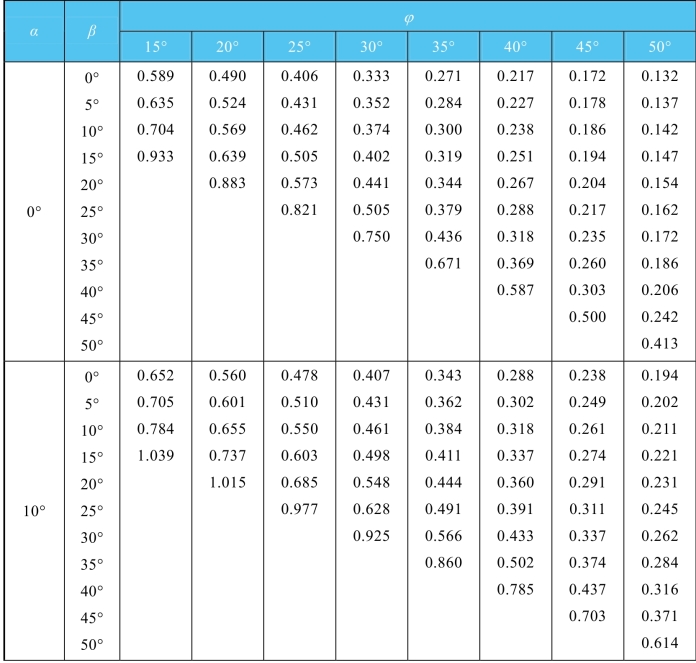
续表

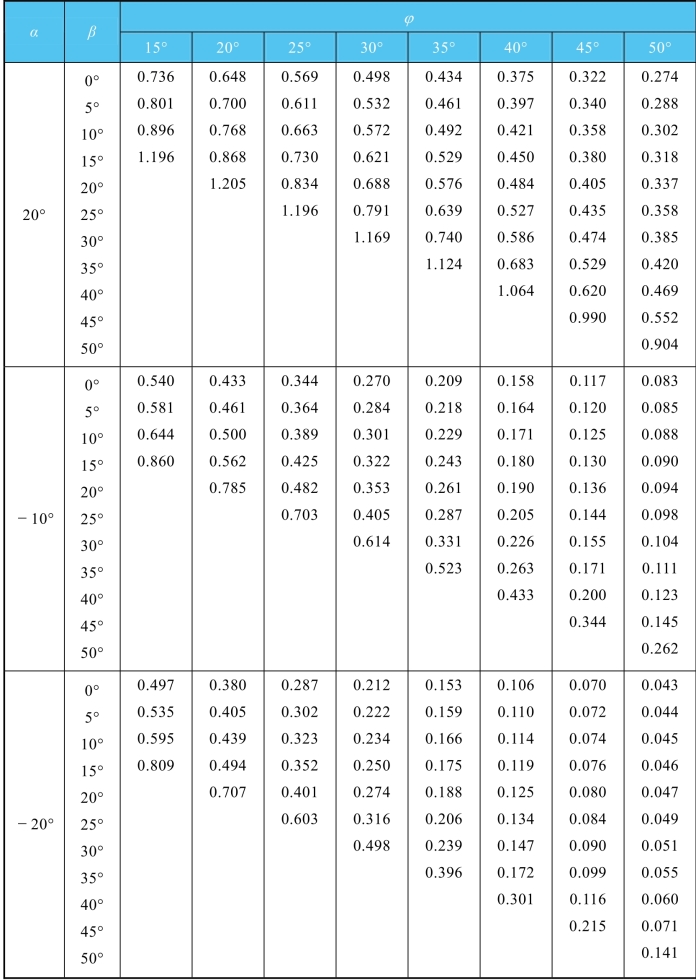
表6-4　主动土压力系数Ka值（δ＝5°）

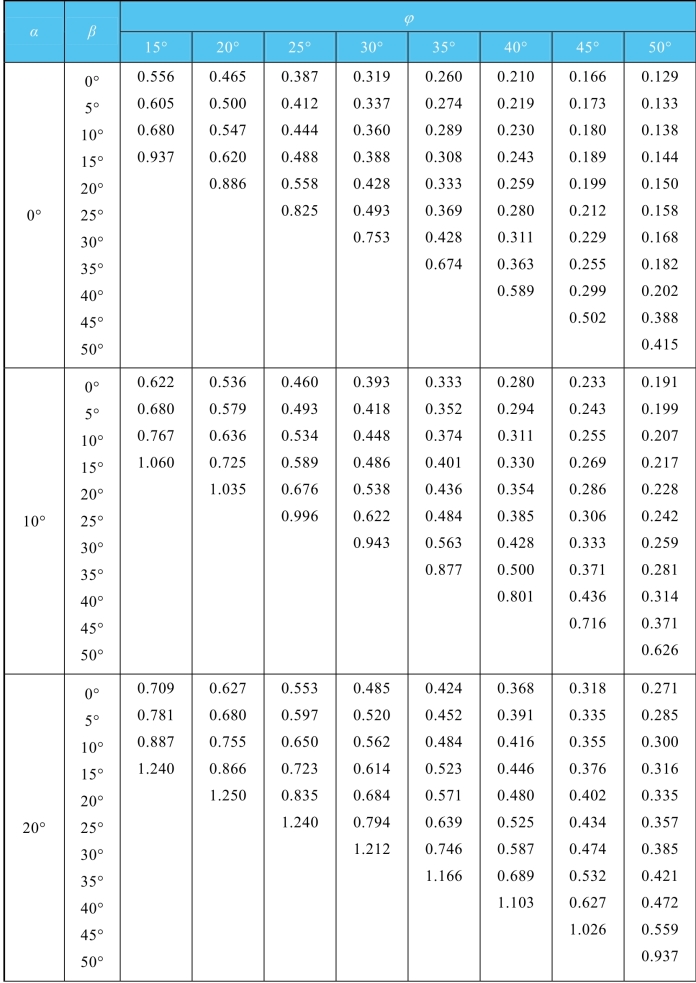
续表(www.xing528.com)

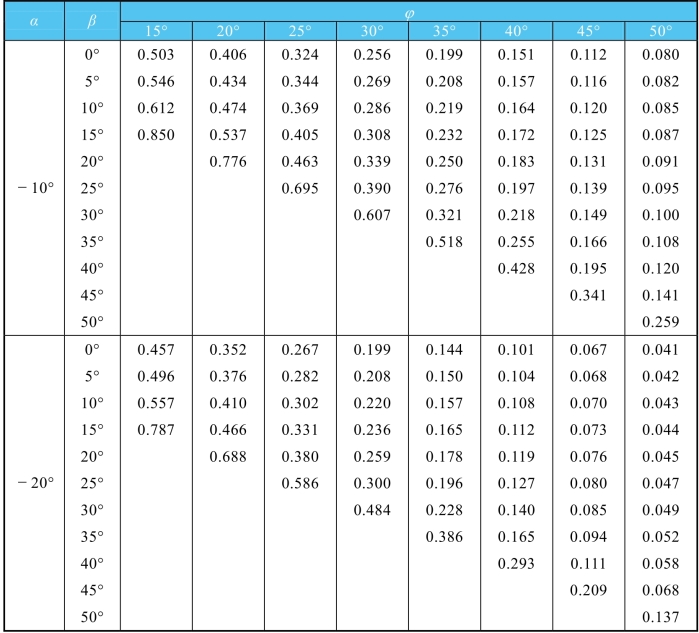
表6-5　主动土压力系数Ka值（δ＝10°）

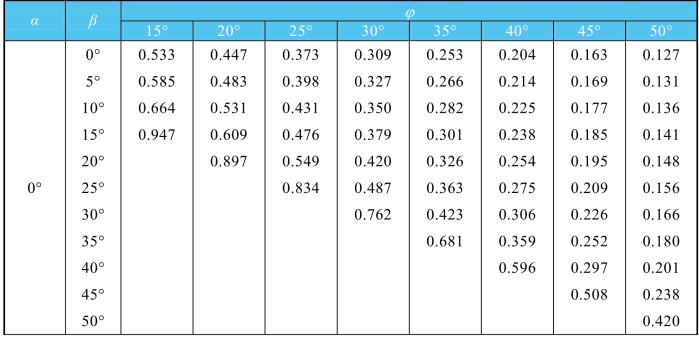
续表

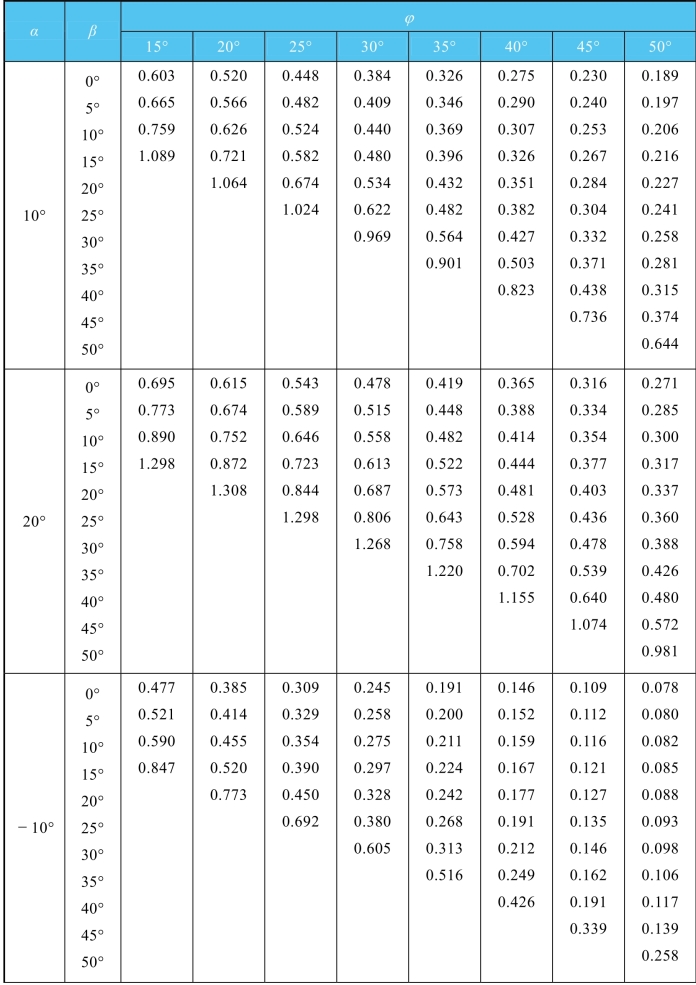
续表

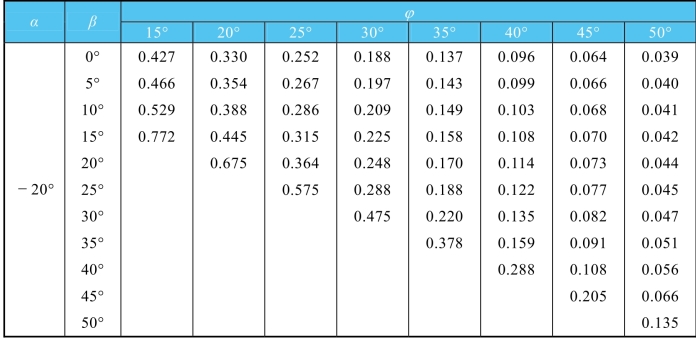
表6-6　主动土压力系数Ka值（δ＝15°）

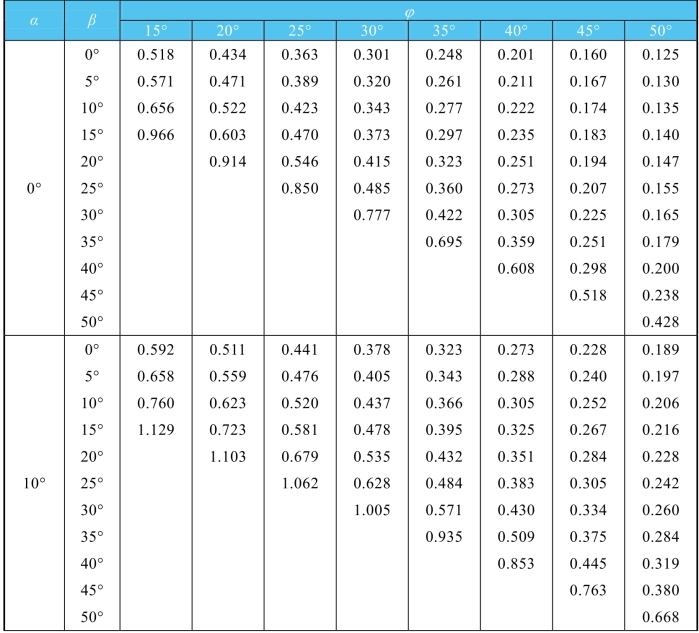
续表

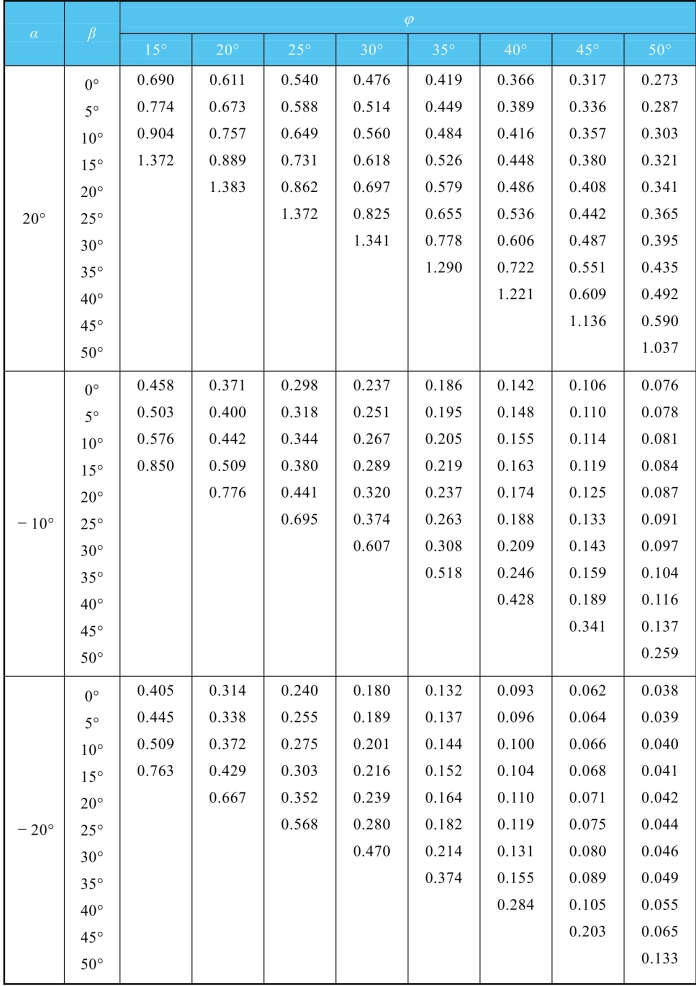
表6-7　主动土压力系数Ka值（δ＝20°）

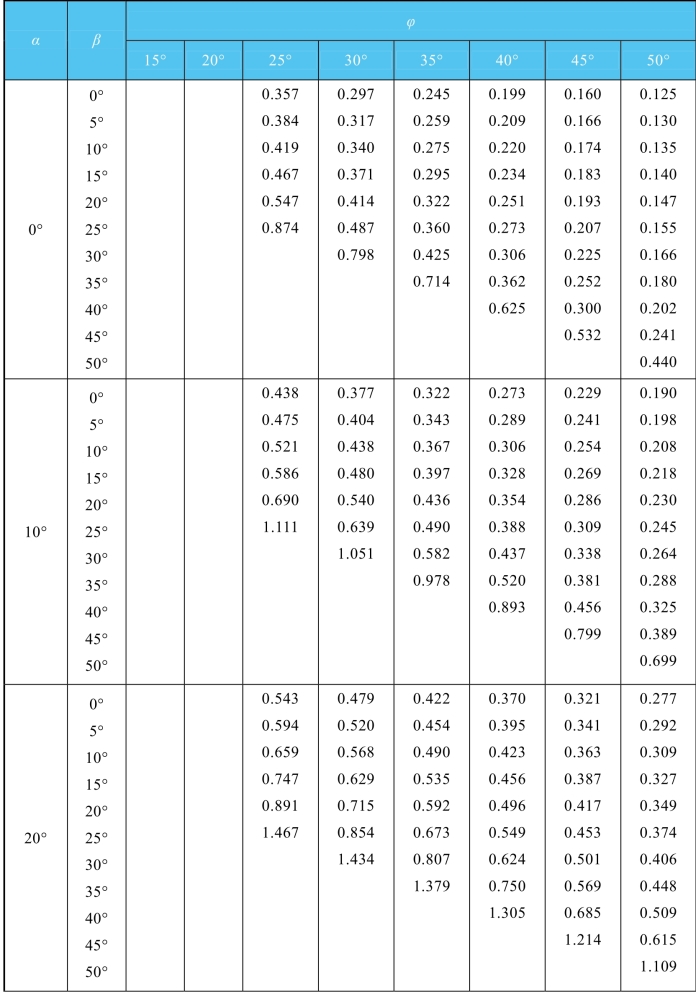
续表

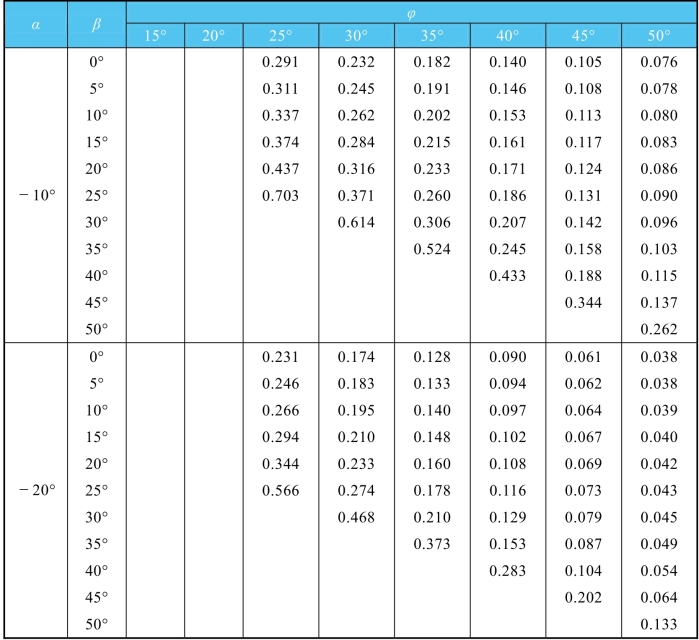
表6-8　主动土压力系数Ka值（δ＝25°）

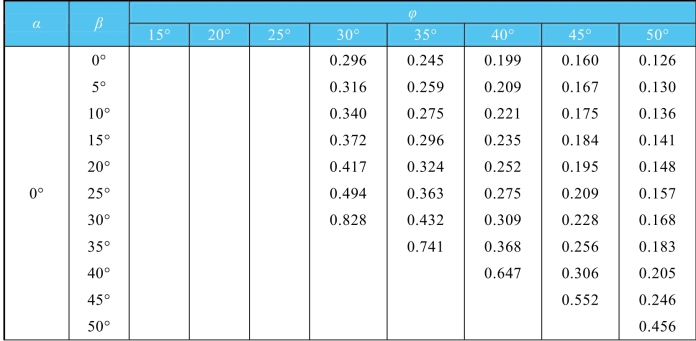
续表

续表

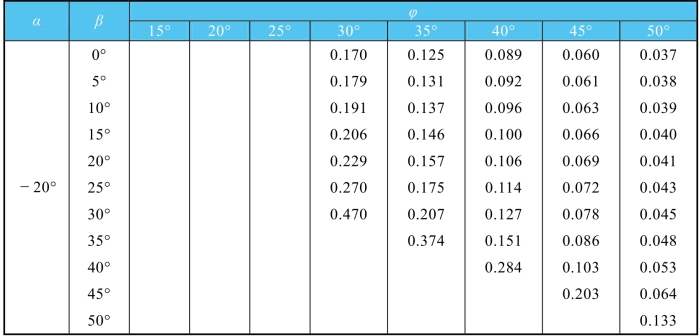
表6-9　土对挡土墙墙背的摩擦角

例题6-5　有一重力式挡土墙高4.0 m，α＝10°，β＝5°，墙后填砂土，c＝0，φ＝30°，γ＝18 kN/m3。试分别求出当δ＝φ/2和δ＝0时，作用于墙背上的总主动土压力Ea的大小、方向及作用点。

解：（1）求时的主动土压力Ea1。

根据α=10°，β=5°，＝15°和φ＝30°，查表6-6，得Ka1＝0.405，则

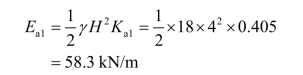
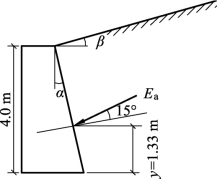
图6-22　例题6-5图

Ea1作用点位置在距墙底H/3处，即y＝4/3＝1.33 m。Ea1作用线与墙背法线的夹角为15°，如图6-22所示。

（2）求δ＝0时主动土压力Ea2。

根据α＝10°，β＝5°，δ＝0°和φ＝30°，查表6-3，得Ka2＝0.431，则

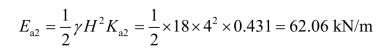
Ea2的作用点与Ea1相同，Ea2的方向为水平指向墙背。

比较上述计算结果可知，当墙背与土之间的摩擦角δ减小时，作用于墙背上的总主动力压力将增大。