朗肯主动土压力计算公式-基于《土力学与地基基础》

如图6-15（a）所示，朗肯主动土压力计算的实质就是已知单元体中的竖向应力为大主应力（即σ1=γz），求极限平衡状态时的水平向小主应力。

1.无黏性土的主动土压力

对于无黏性土（c＝0），我们曾推导过已知大主应力，求小主应力的极限平衡条件为

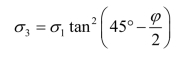
当墙后填土处于主动极限平衡状态时，朗肯主动土压力强度ea为小主应力σ3，而竖向应力为大主应力σ1，则主动土压力强度可表示为

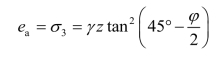
令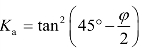，称为朗肯主动土压力系数，则主动土压力强度为

式中　ea——朗肯主动土压力强度（kPa）；

　　　γ——填土的重度（kN/m3）；

　　　z——计算点距填土表面的深度（m）；

　　　φ——填土的内摩擦角（°）。

由上式可见，主动土压力强度ea与墙后填土埋深成正比，沿墙高呈三角形分布，如图6-15（b）所示。

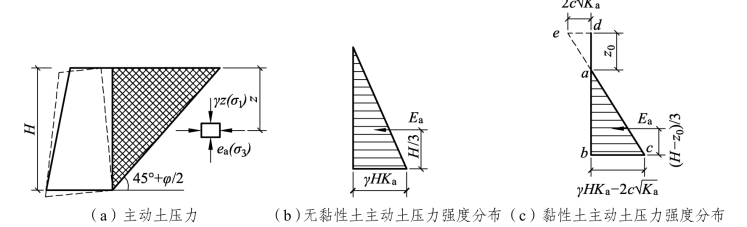
图6-15　无黏性土主动土压力压强分布

单位长度挡土墙上的主动土压力为

Ea的方向为水平指向墙背，作用点在距离墙底H/3处。

2.黏性土的主动土压力

对于黏性土（c≠0），我们也曾推导过已知大主应力，求小主应力的极限平衡条件为

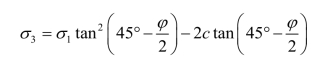
当墙后填土处于主动极限平衡状态时，朗肯主动土压力强度ea为小主应力σ3，而竖向应力为大主应力σ1，则主动土压力强度可表示为

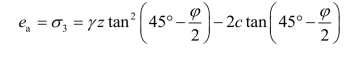
令朗肯主动土压力系数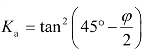，此时的主动土压力强度可表示为(www.xing528.com)

式中　ea——黏性土朗肯主动土压力强度（kPa）；

　　　γ——填土的重度（kN/m3）；

　　　z——计算点距填土表面的深度（m）；

　　　c——土的黏聚力（kPa）；

　　　φ——填土的内摩擦角（°）。

墙后填土为黏土时，朗肯主动土压力强度由正负两部分叠加而成：一部分是由土自重引起的土压力γzKa，为正值；另一部分是由于黏性土内聚力的存在而引起的负侧压力；两者叠加结果如图6-15（c）所示。不难发现，按照土力学中应力正负号的定义习惯，图6-15（c）中aed是负值，对墙背产生拉力，实际上是不存在的，即在z0范围内没有土压力。

式（6-7）中的深度z0，称为临界深度（开裂深度），此处的主动土压力强度为零。这就是许多陡峭的黏土坡不需支撑能直立不坍塌的原因，因此黏性土的主动土压力强度分布图形仅是abc部分。

墙后填土为黏土时，单位长度挡土墙上的主动土压力为

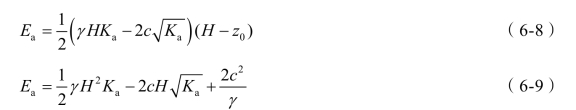
墙后填土为黏土时，主动土压力Ea的方向仍为水平指向墙背，但是其作用点在距离墙底（H-z0）/3处，如图6-15（c）所示。

例题6-3　有一高7 m，墙背直立、光滑，填土表面水平的挡土墙。填土的物理力学性质指标为：c＝12 kPa，φ＝15°，γ＝18 kN/m3。试求挡土墙所受的主动土压力及作用点，并绘制主动土压力强度分布图。

解：（1）主动土压力强度。

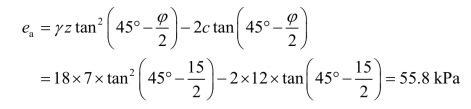
（2）主动土压力合力。

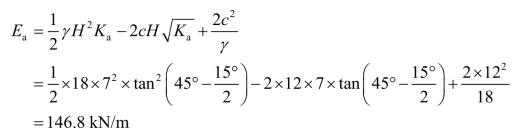
（3）临界深度。

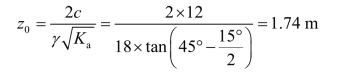
（4）主动土压力作用点距墙底的距离。

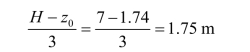
（5）主动土压力分布如图6-16所示。

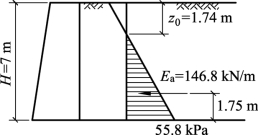
图6-16　例题6-3图