摩尔应力圆解析：土力学与地基基础

现以平面应变问题为例。如图5-7所示，在土中取一单元土体，假设作用在单元土体上的两个主应力为竖向应力σ1（大主应力）和水平应力σ3（小主应力），取任一斜截面mn切割单元土体，斜截面mn与大主应力σ1的作用面（即水平面）成α角，斜截面mn上作用法向应力σ 和剪应力τ。为了表示任意斜截面mn上的法向应力σ 和剪应力τ，截取楔形体abc为研究对象进行静力分析。

图5-7　土体中任意斜面上的应力

将各力分别在水平和垂直方向投影，根据静力平衡条件和F=σA可得

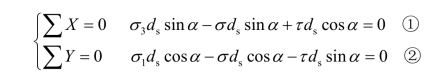
联立求解以上方程，消去斜截面长度ds，①乘以cosα，②乘以sinα，可得

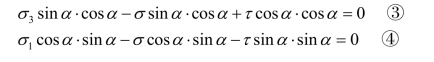
③＋④得到mn平面上的法向应力

③－④得到mn平面上的剪应力

(www.xing528.com)

由式（5-6）和式（5-7）可知，若给定σ1和σ3，则通过该单元体任一平面上的法向应力和剪应力将随着它与大主应力面的夹角α不同而不同。

将式（5-6）移项后两端平方，将式（5-7）两端平方可得

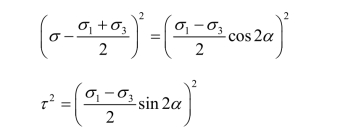
将两式相加可得

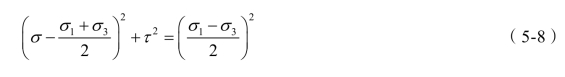
不难看出上述关系式为一个圆的方程式。由式（5-6）和式（5-7）不难发现，式中的σ 和τ 是单元土体任意截面上的法向应力和剪应力，而它们恰好是圆方程式（5-8）的解。因此，在σ-τ坐标平面内，单元土体的应力状态的轨迹是一个圆，圆心坐标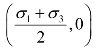，半径为，该圆就称为摩尔应力圆，如图5-8所示。摩尔应力圆上点的横、纵坐标分别代表了单元土体某个截面上的法向应力和剪应力。

在图5-8中，B点坐标为（σ3，0），C点坐标为（σ1，0）。这说明B点和C点所对应截面的法向应力分别为σ3和σ1，它们所对应截面的剪应力则均为0。图5-7（a）中，单元土体的竖直截面和水平截面上的应力恰好为B点和C点的坐标。因此，我们可以认为B点代表竖直面，C点代表水平面。当C点在摩尔应力圆上绕着圆心D转过180°时，刚好到达B点。此时，截面正好由水平面转变为竖直面，即截面转动了90°。于是，可以推测截面在单元土体中转过的角度等于摩尔应力圆上点运动所对应圆心角的一半。这样，只要在图5-8中给出一个确定的点，我们就可以知道这个点所对应的截面及其上的法向应力和剪应力，即摩尔应力圆可以全面表示土体中一点的应力状态。

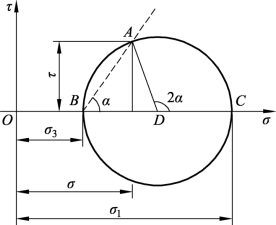
图5-8　土的摩尔应力圆

需要指出，在土力学中画摩尔应力圆时，应力的正负号与材料力学不同，一般规定如下：法向应力以压应力为正，拉应力为负；剪应力以逆时针方向为正，顺时针方向为负。例如：在摩尔应力圆上，纵坐标绝对值最大的点为过圆心D的铅垂线与圆的两个交点。那么，单元土体中剪应力最大值出现在与水平面成±45°的截面上，剪应力最大值为（σ1-σ3）/2。