摩尔-库仑强度理论在土力学与地基基础中的应用

抗剪强度τf与法向应力σ 间呈线性关系。在一般工程压力作用下，τf与σ 可近似地看成直线关系，用库仑定律基本上能满足工程计算的精确要求。然而，在高压力作用下，τf与σ的关系不再是直线而变成弯曲的曲线。此时，库仑定律已不适用，应考虑采用其他的抗剪强度定律。

1910年，摩尔（Mohr）提出材料的破坏是剪切破坏的理论。当任一平面上的剪应力等于材料的抗剪强度时该点就发生破坏，并提出在破坏面上的剪应力，即抗剪强度τf是该面上法向应力的函数，即

由此函数关系所确定的曲线称为摩尔破坏包（络）线，也可称为抗剪强度包线，如图5-6所示。依据计算点的应力值与摩尔抗剪强度包线的关系，可以检验是否达到破坏状态。(www.xing528.com)

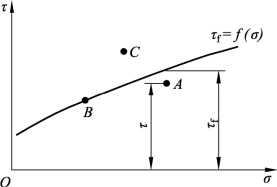
图5-6　摩尔破坏包线

如果代表土单元体中某一个面上法向应力σ 和剪应力τ 的点落在破坏包线下面，如A点，表明在该法向应力σ 下，该面上的剪应力τ 小于土的抗剪强度τf，土体不会沿该面发生剪切破坏。若正好落在破坏包线上，如B点，表明剪切面上剪应力等于抗剪强度，土单元体处于临界破坏状态或极限平衡状态。若位于破坏包线以上，如C点，即处于破坏区域内，表明土单元体已经破坏，实际上这种应力状态是不存在的。当剪应力τ 增加到抗剪强度τf时，将产生应力迁移和应力重分布，不可能再继续增长。当然，土单元体中只要有一个面发生剪切破坏，该土单元体就进入了破坏状态。

理论分析和实验都证明，摩尔理论对土比较合适。在应力变化范围不是很大的情况下，土的摩尔破坏包线通常可以近似地用直线代替，该直线方程就是库仑公式表达的方程，即土的抗剪强度与法向应力呈线性函数的关系。这种以库仑公式作为抗剪强度公式，根据剪应力是否达到抗剪强度作为破坏标准的理论，被称为摩尔-库仑强度理论。