土力学与地基基础中的库仑定律及强度线

如图5-3所示，将一块土样装在有开缝的上、下刚性金属盒内，上盒固定，推动下盒，让土样在预定的（虚线所示）横截面进行剪切，直至土样破坏。破坏时，剪切面上的剪应力就是土的抗剪强度。

试验结果表明，土的抗剪强度不是定值，而是随作用在剪切面上的法向应力σ 的增加而增加。

图5-3　固定剪切面的剪切试验

1—开缝；2—土样；3—上剪切盒；4—下剪切盒。

1776年，法国工程师库仑（Coulomb）根据砂土剪切试验，将土的抗剪强度τf表达为滑动面上法向总应力σ 的函数，即

之后又提出了适合黏性土的更普遍的表达式：

式中　τf——土的抗剪强度（kPa）；

　　　σ——作用在剪切面上的法向应力（kPa）；

　　　φ——土的内摩擦角（°）；

　　　tanφ——土的内摩擦角系数；(www.xing528.com)

　　　σ tanφ——土的内摩擦力（摩阻力）（kPa）；

　　　c——土的黏聚力（内聚力）（kPa）。

式（5-1）和式（5-2）统称为库仑公式，或库仑定律。从该定律可知，对于无黏性土（如砂土），c＝0，可以看作是式（5-2）的一个特例。

库仑定律表明，在法向应力变化不大的范围内，土的法向应力和抗剪强度之间呈直线关系，τf 与σ的关系曲线如图5-4所示，将τf -σ 坐标中的直线称之为库仑强度线。图中直线在纵坐标上的截距即为土的黏聚力c，直线的倾角为内摩擦角φ。

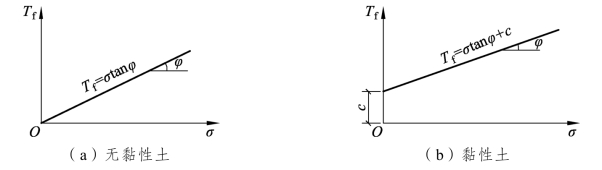
图5-4　土体抗剪强度与法向应力之间的关系

由图5-4可以看出，土的抗剪强度随着法向应力的增大而增大。这与其他固体材料不同，对于其他固体材料，在一般应力范围内，其抗剪强度为一常量，而土的抗剪强度与法向应力成正比，这反映出土体具有散粒体的强度特点。当法向应力增大时，颗粒与颗粒之间被挤压紧密，颗粒之间的滑动摩擦力和咬合摩擦力均增大，若使之发生剪切错动需要更大的剪应力，故抗剪强度大；反之，则小。

根据太沙基（Terzaghi）的有效应力概念，土体内的剪应力只能由土的骨架承担。因此，土的抗剪强度τf 应表示为剪切破坏面上的法向有效应力σ′的函数，库仑公式应修改为

式中　σ′——剪切破坏面上的法向有效应力（kPa）；

　　　c′——有效黏聚力（kPa）；

　　　φ′——有效内摩擦角（°）。

因此，土的抗剪强度有两种表达方法，一种是以总应力σ表示剪切破坏面上的法向应力，抗剪强度表达式即为库仑公式或库仑定律，称为抗剪强度总应力法，相应的c、φ称为总应力强度指标（参数）；另一种则以有效应力σ′表示剪切破坏面上的法向应力，其表达式为式（5-3）、式（5-4），称为抗剪强度有效应力法，c′和φ′称为有效应力强度指标（参数）。试验研究表明，土的抗剪强度取决于土粒间的有效应力。然而，由库仑公式建立的概念在应用上比较方便，许多土工问题的分析方法都还建立在这种概念的基础上，故在工程上仍沿用至今。