成层土渗透性|土力学与地基基础

天然沉积土往往是由渗透性不同的土层组成，宏观上具有非均质性。对于与土层层面平行或垂直的简单渗流情况，当各土层的渗透系数和厚度为已知时，我们可求出整个土层与层面平行或垂直的平均渗透系数，作为进行渗流计算的依据。

1.渗流方向平行于层面（水平向渗流）

已知地基内各层土的渗透系数分别为k1、k2、k3…，厚度相应为H1、H2、H3…，总土层厚度即等效土层厚度为H，如图2-8所示。当渗透水流在水平方向上流动时，渗透距离为L，水头损失为Δh。

图2-8　成层土水平向渗流

这种平行于各层面的水平渗流具有如下的特点：

（1）各层土中的水力坡降i（i=Δh/L）与等效土层的平均水力坡降i相同。

（2）在水平方向取单位宽度，通过等效土层H的总的单宽渗透流量等于各土层渗流流量之和，即

将达西定律代入式（2-13）可得

消去i后，即可得出沿水平方向的等效渗透系数kx。

由上可知，平行于层面的等效渗透系数kx值为各土层渗透系数按厚度的加权平均值。

2.渗流方向垂直于层面（竖向渗流）

对于渗流垂直于土层的情况见图2-9，设承压水流流经土层H厚度的总水头损失为Δh，流经每一层土的水头损失为Δh1、Δh2、Δh3…。

这种垂直于各层面的渗流具有如下特点：

（1）根据水流连续原理，流经各土层的流速与流经等效土层的流速相同，即

图2-9　成层土竖向渗流

(www.xing528.com)

（2）流经等效土层H的总水头损失面Δh等于各层土的水头损失之和，即

将达西定律代入式（2-16），则

从而可解出

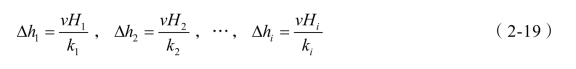
设竖直等效渗透系数为kz，对等效土层有，从而可得

将式（2-19）和式（2-20）代入式（2-17）得

消去v，即可得出垂直于土层方向的等效渗透系数kz为

上式表明，垂直于层面的等效渗透系数kz主要由渗透系数小的土层所控制。

可以证明，对于成层土，水平向平均渗透系数总是大于竖向平均渗透系数，有时可大到10倍左右。

思政小课堂

土体渗透系数的影响因素众多且复杂，因此我们应从多角度出发，分析其对渗透系数的影响规律，提升自身的综合思维、系统思维。

动画—系统思维

系统思维是原则性与灵活性有机结合的基本思维方式。客观事物是多方面相互联系、发展变化的有机整体。系统思维就是人们运用系统观点，把对象的互相联系的各个方面及其结构和功能进行系统认识的一种思维方法。系统思维是一种逻辑抽象能力，也可以称为整体观、全局观。

党的十八大以来，习近平总书记在推进政治、经济、军事、科学、文化等方面的思维和决策，表现出系统思维方法的科学性与系统性。全面深化改革是一项复杂的系统工程，各项工作、各类要素相互交织，牵一发而动全身，只有坚持系统思考，科学统筹，各方面的改革举措良性互动、协同配合，把推进理论创新、制度创新、科技创新、文化创新以及其他各方面创新有机衔接起来，才能形成强大合力，将改革事业顺利推向前进。