流动的液体由于存在黏滞性而具有两种流动形态。为了分析与描述液体的运动,我们一般将液体质点的运动轨迹称为流线。液体质点作有条不紊的运动,液体质点的流线相互平行、不发生交错的形态称为层流;层流的流速一般比较小。液体质点作不规则运动,液体质点的流线相互交错的形态叫作紊流(湍流,乱流);紊流的流速通常较大,且在局部位置可能产生漩涡。
由于土体中孔隙一般非常微小且很曲折,水在土体流动过程中黏滞阻力很大,速度十分缓慢,因此多数情况下其流动状态为层流。
1856年,法国工程师达西(Darcy)利用图2-2所示实验装置对均匀砂进行了大量的渗透实验,得到了层流条件下,土中水的渗透速度与能量(水头)损失之间关系的渗流规律,也就是达西定律,也被称为渗透定律。
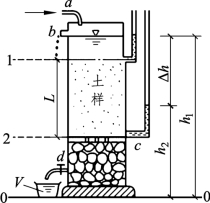
图2-2 达西渗透实验装置
达西实验装置的主要部分是一个上端开口的直立圆筒,下部放碎石,碎石上放一块多孔滤板c,滤板上面放置颗粒均匀的土样,其断面积A,长度为L。筒的侧壁装有两支测压管,分别设置在土样上下两端的水断面1、2位置处。水由上端进水管a注入圆筒,并以溢水管b保持筒内为恒定水位。透过土样的水从装有控制阀门d的弯管流入容器V中。
当筒的上部水面保持恒定后,通过砂土的渗流为恒定流,测压管中的水面将恒定不变,图2-2中的0—0面为基准面,h1、h2分别为1、2断面处的测压管水头。
达西根据对不同尺寸的圆筒和不同类型及长度的土样所进行的实验发现,单位时间内的渗水量q与水力梯度(坡降)i和圆筒断面积A成正比,且与土的透水性质有关,即

式中 q——单位渗水量(cm3/s);(https://www.xing528.com)
v——断面平均渗流速度(cm/s);
i——水力梯度,表示单位渗流长度上的水头损失(Δh/L),或称水力坡降;
k——反应土的透水性的比例系数,称为渗透系数(cm/s)。它相当于水力梯度i=1时的渗透速度,故其量纲与渗透速度相同。
关于达西定律的几点说明:
(1)在层流状态的渗流中,渗透速度v与水力坡降i的一次方成正比,并与土的性质有关。
(2)渗透流速v并不是土孔隙中水的实际平均流速。在公式推导中采用的是土样的整个断面积,其中包括了土粒骨架所占的部分面积在内。土粒本身是不能透水的,实际的过水面积Av应小于A,从而实际平均流速vs应大于v。一般称v为达西流速。
(3)土中水的实际渗流路径是曲折的,比试样长度大得多,而且也无法知道,如图2-3所示。达西考虑了以试样长度计的平均水力梯度,而不是局部的真正水力梯度。

图2-3 水通过土孔隙示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




