柱下条形基础计算问题解析

【规范规定】

《建筑地基基础设计规范》（GB 50007—2011）

8.2.6 扩展基础的基础底面积，应按本规范第5章有关规定确定。在条形基础相交处，不应重复计入基础面积。

8.3.2 柱下条形基础的计算，除应符合本规范第8.2.6条的要求外，尚应符合下列规定：

1.在比较均匀的地基上，上部结构刚度较好，荷载分布较均匀，且条形基础梁的高度不小于1/6柱距时，地基反力可按直线分布，条形基础梁的内力可按连续梁计算，此时边跨跨中弯矩及第一内支座的弯矩值宜乘以1.2的系数。

2.当不满足本条第1款的要求时，宜按弹性地基梁计算。

3.对交叉条形基础，交点上的柱荷载，可按静力平衡条件及变形协调条件，进行分配。其内力可按本条上述规定，分别进行计算。

4.应验算柱边缘处基础梁的受剪承载力。

5.当存在扭矩时，尚应作抗扭计算。

6.当条形基础的混凝土强度等级小于柱的混凝土强度等级时，应验算柱下条形基础梁顶面的局部受压承载力。

【解析】

依照上部结构刚度的大小，可将简化计算法分为静定分析法与倒梁法两种，这两种方法均假设基底反力为直线（平面）分布。为满足这一假设，就要求条形基础具有足够的相对刚度。

当柱距相差不大时，要求基础上的平均柱距l_m应满足以下条件：

式中 1/λ——文克勒地基上梁的特征长度；

λ——梁的柔度特征值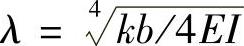，（为方便求解文克勒地基上梁的挠曲微分方程，令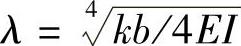，其中，E为梁材料的弹性模量；I为梁的截面惯性矩；b为梁的宽度）。对一般柱距及中等压缩性的地基，按上述条件进行分析，条形基础的高度应不小于平均柱距的1/6。

若上部结构的刚度很小（如单层排架结构），则应采用静定分析法。计算时先根据直线分布假定求出基底净反力，然后将柱荷载直接作用在基础梁上。这样，基础梁上所有的作用力就都已确定，所以可按静力平衡条件计算出任一截面i上的弯矩M_i与剪力V_i，如图5-1所示。因为静定分析法假定上部结构为柔性结构，也就是不考虑上部结构刚度的有利影响，所以在荷载作用下基础梁将会产生整体弯曲。同其他方法相比，这样计算所得到的基础不利截面上的弯矩，其绝对值可能会偏大很多。

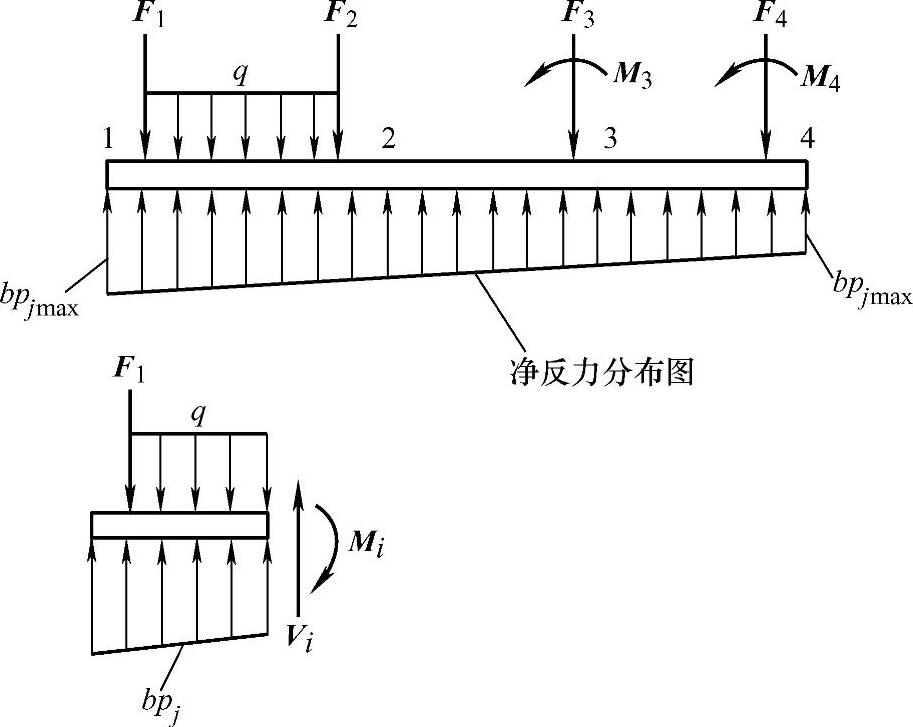
图5-1 按静力平衡条件计算条形基础的内力

倒梁法假定上部结构是绝对刚性的，各柱之间没有沉降差异，所以可以将柱脚视为条形基础的铰支座，将基础梁视为倒置的普通连续梁（采用弯矩分配法或弯矩系数法）来计算，而荷载则为直线分布的基底净反力bp_j（kN/m）以及除去柱的竖向集中力之外所余下的各种作用（包括柱传来的力矩），如图5-2所示。此种计算方法只考虑出现在柱间的局部弯曲，而略去沿基础全长发生的整体弯曲，因此所得的弯矩图正负弯矩最大值比较均衡，基础不利截面的弯矩最小，故倒梁法对于上部结构刚度很大的情况比较适用。

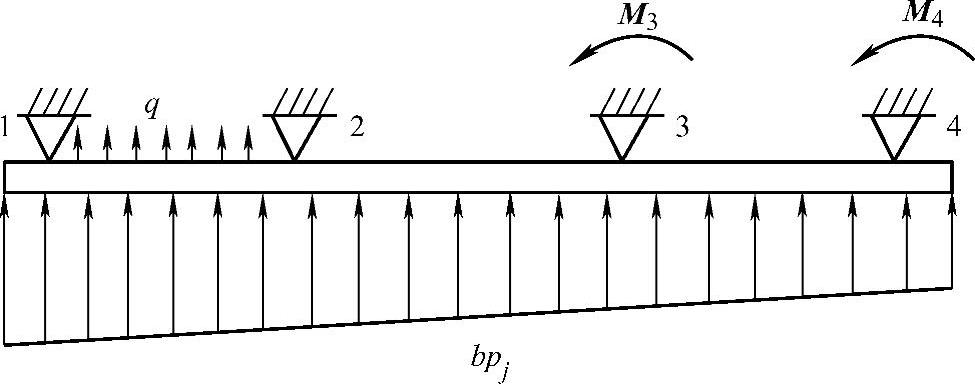
图5-2 倒梁法计算简图

综上所述，在比较均匀的地基上，上部结构刚度较好，荷载分布及柱距较均匀（如相差不超过20%），并且条形基础梁的高度不小于1/6柱距时，基底反力可按直线分布，基础梁的内力可按照倒梁法进行计算。

当条形基础的相对刚度较大时，因为基础的架越作用，其两端边跨的基底反力会有所增大，所以两边跨的跨中弯矩及第一内支座的弯矩值宜乘以1.2的增大系数。需要指出的是，当荷载较大、土的压缩性较高或基础埋深较浅时，随着端部基底下塑性区的开展，架越作用将减弱、消失，甚至会出现基底反力从端部向内转移的情况。

柱下条形基础的计算步骤如下：(www.xing528.com)

（1）确定基础底面尺寸

将条形基础视为一狭长的矩形基础，其长度l主要依据构造要求确定（只要确定伸出边柱的长度），并尽量使荷载的合力作用点重合于基础底面形心。

当轴心荷载作用时，基底宽度b为

当偏心荷载作用时，先按照式（5-2）初定基础宽度并适当增大，然后按照式（5-3）验算基础边缘压力：

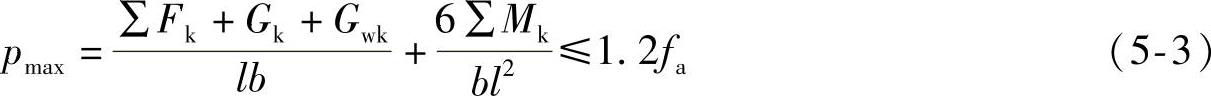
式中 ∑F_k——相应于荷载效应标准组合时，各柱传来的竖向力之和；

G_k——基础自重和基础上的土重之和；

G_wk——作用在基础梁上墙的自重；

∑M_k——各荷载对基础梁中点的力矩代数和；

d——基础平均埋深；

h_w——当基础埋深范围内有地下水时，基础底面到地下水位的距离；无地下水时，h_w=0；

f_a——修正后的地基承载力特征值。

（2）基础底板计算

柱下条形基础底板的计算方法同墙下钢筋混凝土条形基础。在计算基底净反力设计值时，要考虑荷载沿纵向和横向的偏心。当各跨的净反力相差较大时，可对各跨底板依次进行计算，净反力可取本跨内的最大值。

（3）基础梁内力计算

1）计算基底净反力设计值。沿基础纵向分布的基底边缘最大和最小线性净反力设计值可按下式进行计算：

式中 ∑F——各柱传来的竖向力设计值之和；

∑M——各荷载对基础梁中点的力矩设计值代数和。

2）内力计算。当上部结构刚度很小时，可按静定分析法计算；若上部结构刚度较大，则按照倒梁法计算。

采用倒梁法计算时，由于反力呈直线分布及视柱脚为不动铰支座都可能不符合事实，另外上部结构的整体刚度对基础整体弯矩有抑制作用，使柱荷载的分布均匀化，因此计算所得的支座反力通常不等于原有的柱子传来的轴力。若支座反力同相应的柱轴力相差20%以上，可以采用实践中提出的“基底反力局部调整法”进行调整。

肋梁的配筋计算与一般的钢筋混凝土T形截面梁类似，即对跨中按T形、对支座按矩形截面计算。当柱荷载对单向条形基础有扭力作用时，应作抗扭计算。

静定分析法与倒梁法实际上代表了两种极端情况，且有很多前提条件。所以，在对条形基础进行截面设计时，切不可拘泥于计算结果，而应结合具体实际情况和设计经验，在配筋时作相应调整。