【摘要】:图10.2抗剪强度与法向应力的关系曲线无黏性土;黏性土上述土的抗剪强度数学表达式,也称为库仑定律,它表明在一般应力水平下,土的抗剪强度与滑动面上的法向应力之间呈直线关系。这一基本关系式能满足一般工程的精度要求,是目前研究土的抗剪强度的基本定律。
土体发生剪切破坏时,将沿着其内部某一曲面(滑动面)产生相对滑动,而该滑动面上的剪应力就等于土的抗剪强度。1776年,法国学者库仑根据砂土的试验结果 [图10.2(a)],将土的抗剪强度表达为滑动面上法向应力的函数,即
![]()
以后库仑又根据黏性土的试验结果[图10.2 (b)],提出更为普遍的抗剪强度表达形式,即
![]()
式中 τf——土的抗剪强度,kPa;
σ——剪切滑动面上的法向应力,kPa;
c——土的黏聚力,kPa;
ψ——土的内摩擦角,(°)。(https://www.xing528.com)
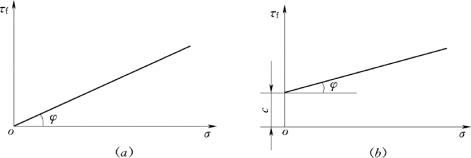
图10.2 抗剪强度与法向应力的关系曲线
(a)无黏性土;(b)黏性土
上述土的抗剪强度数学表达式,也称为库仑定律,它表明在一般应力水平下,土的抗剪强度与滑动面上的法向应力之间呈直线关系。这一基本关系式能满足一般工程的精度要求,是目前研究土的抗剪强度的基本定律。
上述土的抗剪强度表达式中采用的法向应力为总应力σ,称为总应力表达式。根据有效应力原理,土中某点的总应力σ等于有效应力σ′和孔隙水压力u之和,即σ=σ′+u。
若法向应力采用有效应力σ′,则可以得到如下抗剪强度的有效应力表达式

式中 c′、ψ′——有效黏聚力和有效内摩擦角,统称为有效应力抗剪强度指标。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




