CAE分析内容及NASTRAN的SOL111应用

在汽车开发过程中，CAE分析涉及大量的内容，主要可分为模态分析、传递函数分析、优化分析和实车响应分析等，下面分别阐述。

1.模态分析

模态分析包括整车级别和零部件级别。整车模态分析使用整车模型，可不包含声腔模型。模态的结果重点关注车身的刚体模态，如上下跳动、侧倾，动力总成的刚体模态，车身弯曲模态、扭转模态，排气系统的弯曲模态等。这些模态值都要写入整车模态规划表，用来指导整车的NVH设计。

整车模型自由度大，一般可达到500万数量级以上，对计算软件、硬件要求高，需要使用专业服务器。计算时一般使用通用结构分析软件NASTRAN，市场上还有一些专门能提高计算速度的辅助软件，能大大提高NASTRAN的计算速度。

除整车模态分析以外，还包括TB模型分析、白车身模态分析、排气系统模态分析、转向系统模态分析以及更低级别的零部件模态分析。每一个分析项目都有其目标值，分析的结果应该满足目标值的要求，否则要更改结构，采取优化措施。

模态分析有时还可以用来检查模型。如白车身模型组装完成后，进行约束或者自由模态分析。如果是约束模态分析，则结果中不应该含有刚体模态。如果是自由模态分析，则结果中应该包含6个刚体模态。否则，就说明模型中有零件处于未连接状态。另外，在计算过程中，还可以对单元的质量、控制语句等加以检查。当有错误时，软件会中止计算，并在结果文件中提供错误信息，供查找错误。

2.振动传递函数分析

振动传递函数用来评价车身受到激励时的响应水平。激励点一般选取悬置安装点、排气吊挂安装点、悬架安装点等，如图21-12所示。响应点则选取与乘员肢体接触的部位，如转向盘、座椅导轨、地板等处。

计算时使用NASTRAN的SOL111（频率响应分析），可同时计算多个工况，每个工况定义一个方向的激励及多个响应点，结果输出的是加速度。图21-45所示为振动传递函数的计算结果，激励点是发动机左悬置安装点，响应点是转向盘的上端，结果共包含了三个工况。

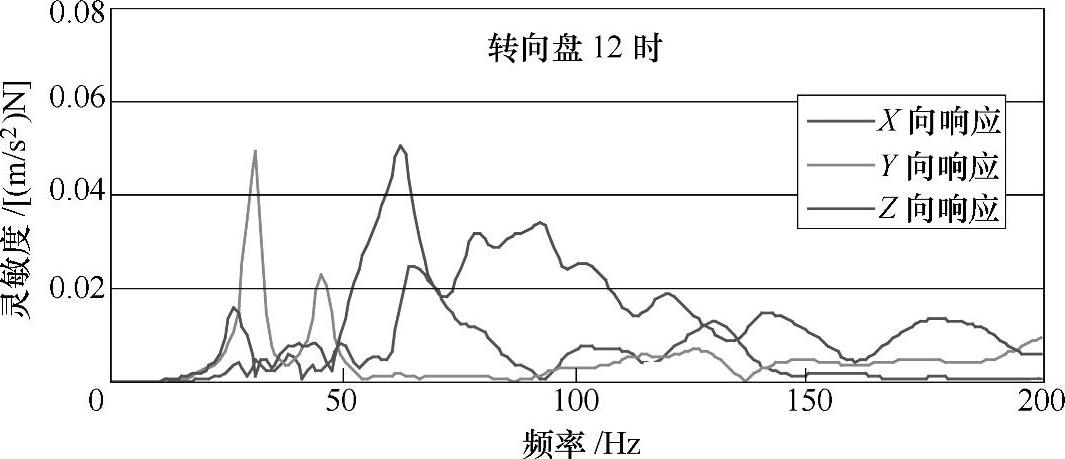
图21-45 振动传递函数计算结果

结果的评价按照规范进行。车身上不同位置的评价指标是不同的，如：

转向盘：VTF≤0.3（m/s²）/N

地板、座椅导轨：VTF≤0.1（m/s²）/N

计算结果中不满足目标要求的点，需要查找原因。通常需要检查激励点是否有局部模态、主要传递路径上是否存在局部模态、曲线峰值是否对应整体模态以及响应点是否存在局部模态等。选择优化方案时，包括提高激励点动刚度、增加响应点阻尼、在适当位置使用动态减振器等手段。

3.声学传递函数分析

声学传递函数用来评价车身受到激励时车内的声压响应水平。激励点一般选取悬置安装点、排气吊挂安装点、悬架安装点等，如图21-12所示。响应点则选取乘员耳边附近，如驾驶人耳旁、后排乘员耳旁等处。

计算时使用NASTRAN的SOL111（频率响应分析）。可同时计算多个工况，每个工况定义一个方向的激励及多个响应点，结果输出的是声压。图21-46所示为声学传递函数的计算结果，激励点是发动机左悬置安装点，响应点是第二排座椅中间位置，结果共包含了三个工况。

结果的评价按照规范进行。不同的激励点的评价指标是不同的，如：

发动机悬置安装点、悬架安装点：NTF≤55dB/N

图21-46 声学传递函数计算结果

排气吊挂安装点：NTF≤60dB/N

计算结果中不满足目标要求的点，需要查找原因。通常需要检查激励点是否有局部模态、主要传递路径上是否存在局部模态、曲线峰值是否对应整体模态以及响应点是否存在局部模态等。选择优化方案时，包括提高激励点动刚度、增加响应点阻尼、在适当位置使用动态减振器等手段。

4.动刚度分析

动刚度是用来评价车身受到激励时的响应水平。评价点如图21-12中的车身硬点，这些点是车身的主要受力点。

计算时使用NASTRAN的SOL111（频率响应分析），可同时计算多个工况，每个工况定义一个方向的激励及一个响应点，结果输出的是加速度，通过公式转化为刚度。图21-47所示为动刚度计算结果。

图21-47 动刚度计算结果

结果的评价按照规范进行，不同的激励点的评价指标是不同的，如主要激励方向不低于10000N/mm，次要受力方向不低于5000N/mm，有时还要同标杆车作对比，相同的点的动刚度水平不应该低于标杆车。同时还要观察动刚度曲线在整个频率范围内是否有明显的高于目标值的峰值。

计算结果中不满足目标要求的点，需要查找原因。通常需要检查激励点是否有局部模态、主要传递路径上是否存在局部模态、曲线峰值是否对应整体模态以及响应点是否存在局部模态等。选择优化方案时，包括提高激励点动刚度、增加响应点阻尼、使用动态减振器等手段。

5.实车响应分析

实车响应是指车辆在路面上行驶，受到动力总成或者路面的激励时的响应。它不同于传递函数分析，传递函数是车身受到单位激励时的车身响应，它只反映了车身的振动特性，不包含激励的特性。实际上车身受到的激励是各种各样的，有不同的幅值、不同的频率。如动力总成的激励是与转速有关的，当发动机转速越来越高的时候，激励也越来越大。在激励中所包含的频率成分也不同，它取决于发动机的类型。直列四缸发动机的2阶成分最大，其次是4阶、6阶，奇数次成分互相抵消。激励的种类也各不相同，四缸发动机的激励主要是上下方向的跳动和绕曲轴中心的旋转力矩，3缸机则主要是绕曲轴中心的旋转力矩（Roll）、绕垂直轴的横摆力矩、绕前后轴的俯仰力矩。

车辆的实际响应等于激励与传递函数的乘积。假设车体受m个激励力作用，每一个激励力都有x，y，z三个方向分量（下面分别用k=1，2，3表示），每一个激励力分量对应着n个特定的传递路径，那么这个激励力分量和对应的某个传递路径就产生一个系统响应分量。以车内噪声声压作为系统响应，这个声压分量可以表示为

式中，T_mnk是传递函数；f_nk是激励。

车内声腔受某个激励力作用，传递过来的所有声压成分之和可以表示为

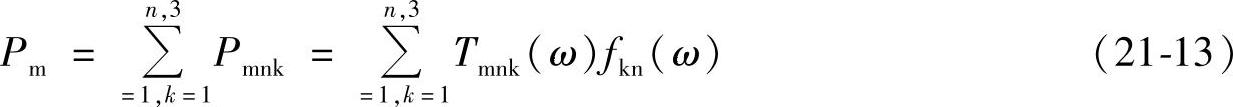
车内声腔受所有激励力作用，传递过来的所有声压成分之和可表示为

（1）怠速响应 怠速时，车身受到的激励主要来自于发动机。获取发动机激励有两个渠道，一是通过试验测试，二是通过计算。发动机激励的理论计算方法已在第四章中详细介绍，此处仅对测试方法加以阐述。

发动机处于怠速工况时，车辆处于静止状态，车身受到的激励主要来自于发动机。发动机的振动通过悬置、排气吊挂传递到车身，车身受到的激励也就是悬置、吊挂等弹性元件的变形力。

图21-48 悬置传递力测试

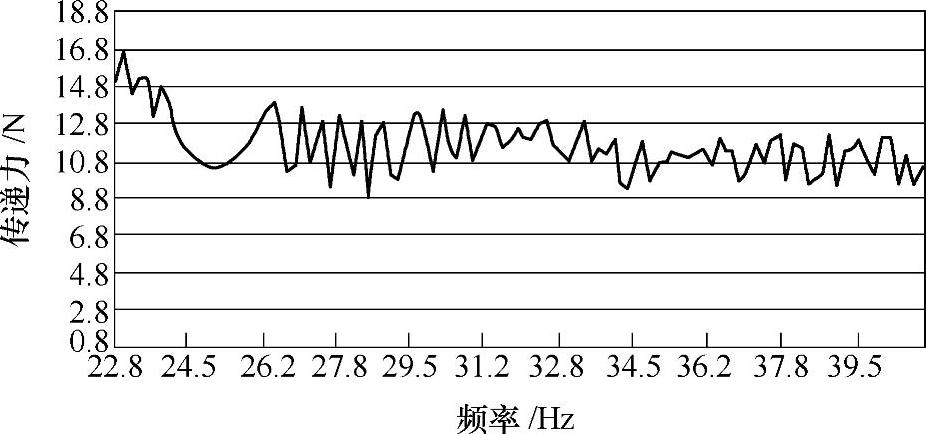
图21-49 发动机主悬置传递力测试结果

测试时，在弹性元件的两端，一端为主动边，一端为被动边，分别粘贴加速度传感器，记录一定时间段内的振动。图21-48为测试示意，a_a为主动边，a_p为被动边，加速度经过两次积分后得到位移，再乘以弹性元件的刚度，即得到了力。图21-49为某车型的发动机主悬置Z向传递力，它代表了发动机工作时通过主悬置向车身所传递的力。

激励乘以传递函数，得到某一传递路径的响应，将所有激励和所有方向的响应加起来，就得到了总的响应，包括振动和噪声。图21-50为怠速时驾驶人座椅导轨处振动（X、Y、Z三个方向），图21-51为怠速时驾驶人右耳附近噪声声压级。

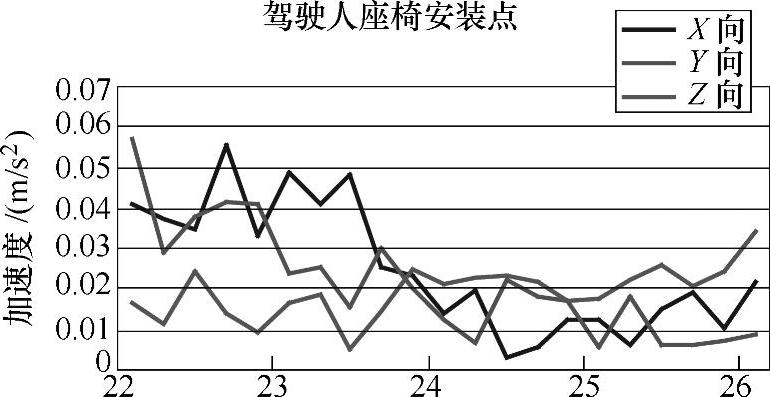
图21-50 怠速振动

图21-51 怠速噪声

车辆怠速工况时的激励和传递路径多且复杂，难以通过计算的方式得到准确的结果。如发动机的激励不仅仅是2阶成分（四缸发动机），还包括4阶、6阶，以及因气缸内不完全燃烧、气门冲击等产生的半阶次激励。传递路径除前面提到的悬置和排气吊挂外，还有如散热器支架、空调配管、进气系统支架和线束等。这些激励和传递路径在模拟和测试时难以一一顾到。因此，无论是测试还是计算模拟，所得到的振动噪声响应只是实际响应的主要部分，而不是全部。

（2）路面噪声。为了预测路面噪声，需要得到路面传递给车身的激励力。但是，路面噪声是由路面非周期性的激励力产生的，在进行数值模拟时，难以精确地输入激励力。在工程上，一般是通过试验的方法来测定车轴位置的激励力。但是这种方法有以下两点难点：依赖于悬架的特性和测量实验条件难以保证。

因此，这种方法在悬架的选择阶段难以适用。基于此，一种新的定义，即等价路面粗糙度在工程上得到了推广，该数据容易获得，不依赖于悬架的特性，主要取决于轮胎的类型及路面的种类。以其为激励源，对路面噪声进行预测，其计算有效性得到了确认。

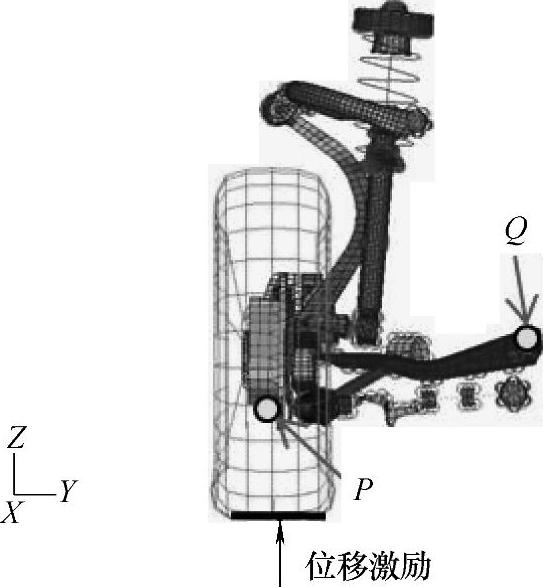
图21-52 半托臂式悬架

①等价路面粗糙度的定义。如图21-52所示，以安装195/60R15轮胎的半托臂式悬架为对象进行等价路面粗糙度的定义。测量点为图中的点P。点P的振动加速度为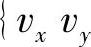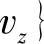，它等于路面传递给轮胎的激励力与轮胎接地面到点P的振动传递率的乘积。此处，路面带来的激励力是关于频率的位移函数，有如下关系式

式中，为轮胎接点同时激励时，从接地点到点P的振动传递率矩阵。

对式（21-15）进行矩阵变换，接地点到点P的振动对角线矩阵可以表示为

此处，假设路面传来的激励力的各方向成分之间不相关，如。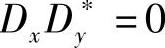

式（21-16）的左边，是车辆行驶时测量得到的加速度对角线矩阵，另外，传递率也可通过测量得到。如上所述，根据式（21-16）进行转换，可以得到

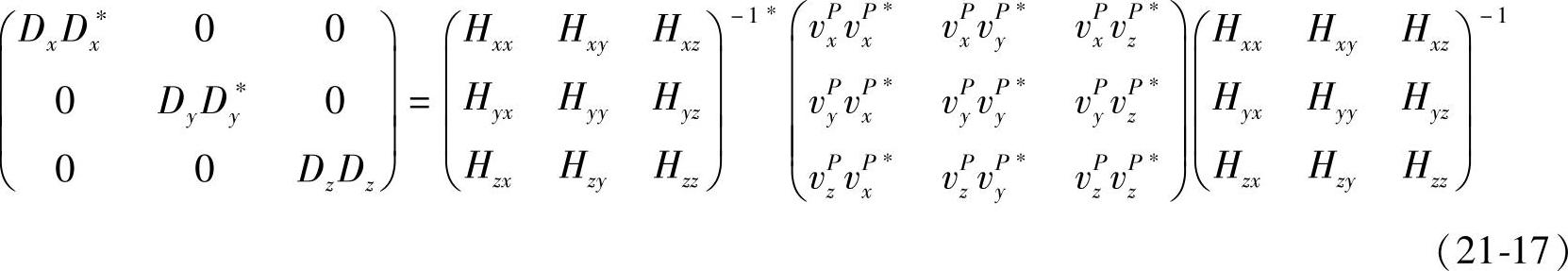
等式的左边定义为等价路面粗糙度。

图21-53 加速度能量频谱

图21-54 等价路面粗糙度

图21-53所示为以车速50km/h行驶时加速度能量谱。图21-54是在静止状态下轮胎接地面全体一起激励时从接地点到点P的振动传递率。基于这些数据而计算出来的路面粗糙度如图21-55所示。从这些图中可以看出，Z方向的等价路面粗糙度同其他方向相比幅值高，对路面噪声的贡献量最大。

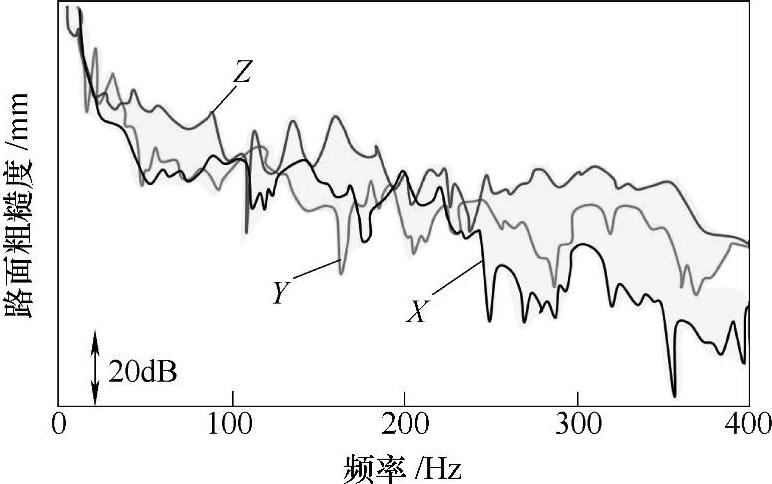
图21-55 等价路面粗糙度

为了对以上计算结果进行验证，对图21-52中所示的Q点振动按照式（21-18）进行计算，其结果如图21-56所示。

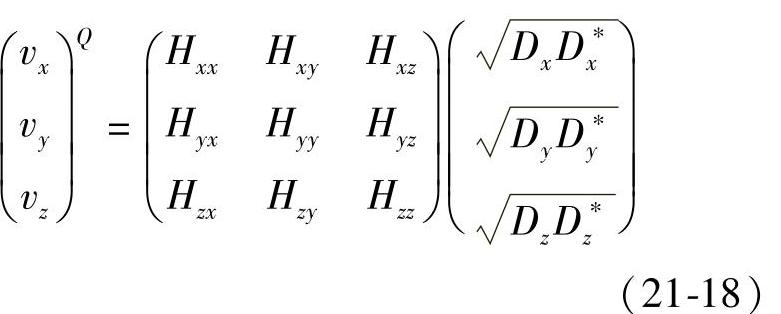
从图中可以看出，计算结果与实验结果有很好的一致性，即计算方法的精度得到了确认。

在前言部分提到，等价路面粗糙度不受悬架的特性影响，仅与轮胎刚度和路面粗糙度相关。为了对此进行验证，在一款多连杆式悬架上安装了同一轮胎，对等价路面粗糙度进行计算，车辆行驶条件同前述一致。

计算结果与半托臂式悬架进行的对比如图21-57所示。从图中可以看出，计算结果虽然略有差别，但是对路面噪声的贡献量，同前面的分析结论是一致的。

图21-56 计算值与实验值的比较(www.xing528.com)

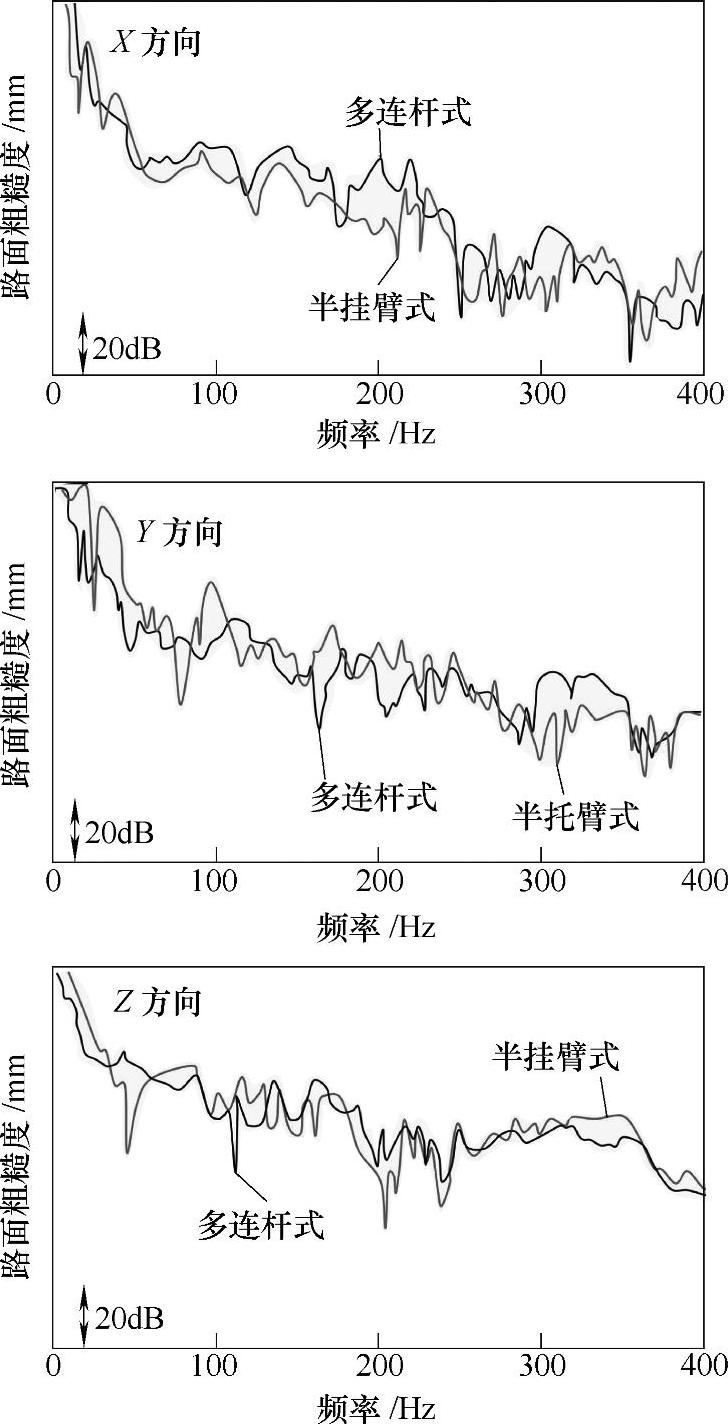
图21-57 不同类型悬架的等价路面粗糙度比较

因此，本文中提出的等价路面粗糙度的概念在悬架的选型设计阶段的应用得到了验证。

②数值计算。在新车开发的悬架系统设计阶段，可以利用前述的等价路面粗糙度的方法，利用数值模拟的方法来进行选择。

表21-2 分析条件

假设在现有的半托臂式悬架基础上，新设计一款多连杆式悬架，可以按照表21-2中的条件进行悬架安装点振动和车内噪声计算。

使用轮胎和悬架系统的有限元模型，考虑车载状态下的轮胎变形，以及悬架系统的结构，首先计算轮胎接点到悬架与车身连接点的传递函数。并利用车身进行敲击试验，分别获得悬架各安装点的振动传递函数、悬架和车身安装点的声学传递函数。最终利用这些测量得到的数据，预测悬架系统振动和车内噪声。

图21-58 车体振动

图21-59 车内噪声

图21-58和图21-59为车辆以50km/h行驶时，振动和车内噪声的测试和计算结果的对比。

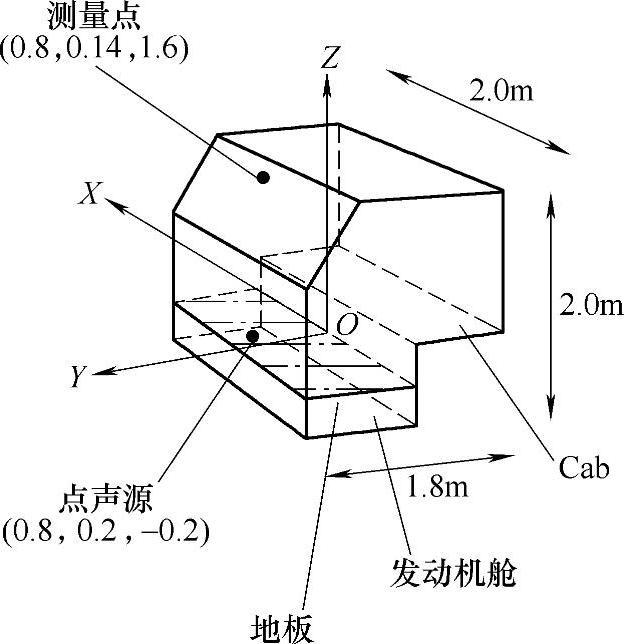
图21-60 分析用模型

6.优化分析

车辆在开发过程中，需要设定各种目标，如模态、动刚度、传递函数和实车响应等。对于不满足目标值要求的项目要对车身结构进行调整，采取优化措施，以满足目标。优化分析的种类很多，具体的问题要具体对待。所使用的模型、分析方法、最终采取的措施等，不但要满足既定的目标值要求，还不能使已有的性能指标下降，如强度耐久、碰撞安全性等。最重要的是要尽可能使所增加的重量控制在一定的范围内。

下面结合一个实际的案例，来介绍优化方法的应用。通过对驾驶室地板的曲面形状优化，来达到降低驾驶室内特定位置的低频声压的目的。而在此之前，需要确定驾驶室各部位对轰鸣噪声的贡献量。分析的时候，使用的是驾驶室的简易模型，采取流固耦合有限元分析方法，进行地板的结构优化。

（1）分析模型 图21-60所示为分析用的简易模型及边界条件。模型由驾驶室的结构部分和驾驶室内的空气部分组成。驾驶室模型由shell单元组成，声腔模型由solid单元组成，驾驶室壁板厚为1.5×10^-3m，为常用的钢板锻压而成。音速为340m/s，减衰比为0.02。在发动机舱内的（0.8，0.2，-0.2）处设置一个点声源，从1～150Hz每隔1Hz做一次声压激励。另外，在乘员的头部附近（0.8，0.14，0.16）处设置声压测量点。

从声源中放射出来的声压，转换为驾驶室壁板的振动透射到驾驶室内，同时诱发发动机舱内的声腔模态，在共振的作用下，发动机舱内的声压被大幅度放大并作用到车身壁板上，引起车身壁板的强制振动。在此强制振动下，压迫驾驶室的空气，当强制激励力与驾驶室内的声腔模态耦合时，室内的声压又被增幅，从而在驾驶室内产生强烈的轰鸣声压迫乘员的耳膜，使人产生不舒服的感觉。

在密闭空间内的声激励引起的结构弹性振动，必须要进行结构与声腔的耦合分析。发动机舱和驾驶室内这两个声腔和结构之间的振动耦合分析，通常在忽略阻尼减衰时，可以用下式表示

式中，s、a分别为结构、声腔系的下脚标；w为结构的位移；p为声压；f=为激励力；M为质量行列式；K为刚度行列式；A为耦合矩阵。模型的求解使用MSC/NASTRAN。

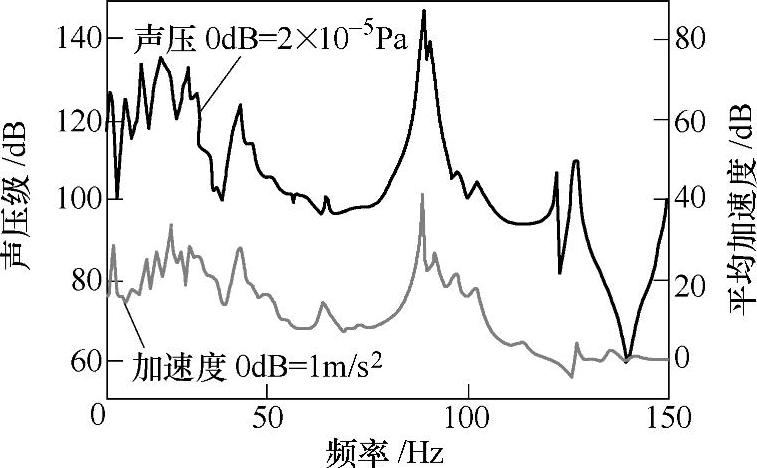
图21-61 声压及平均振动加速度

图21-61中是地板位置的空间平均振动加速度和声压测量点的声压频率响应计算结果。

通过比较声压和振动加速度的结果，峰值点、幅值并没有完全对应，这是因为地板板件以外的驾驶室其他部分的振动特性与驾驶室声腔模型之间的耦合振动的影响造成的。89Hz时的声压幅值特别高，与其对应的位置出现了很明显的振动峰值。分析认为是由于结构与声腔的模态耦合造成了驾驶室内的声压增幅。

考虑一个长方形的封闭空间，假设其各个壁面为刚性，不考虑结构与声腔的耦合。那么，声腔的共振模态通常可用下式求得

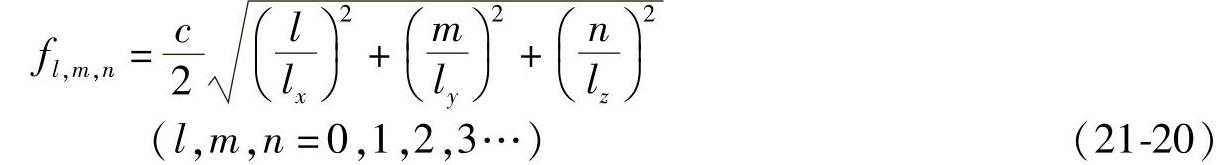
式中，c为声速；l_x，l_y，l_z为长方体的长、宽和高。上面的声压峰值频率与驾驶室内声腔左右（X）方向的1次共振模态对应。另外，此时驾驶室内的声压分布如图21-62所示。

图21-62 共振时的声压分布

（2）加强筋的效果 对驾驶室内轰鸣音贡献量最大的当属地板，通过采取结构优化可以改善车内的噪声。我们知道，抑制结构表面的振动能有效降低结构振动引起的噪声。因此，通过提高地板件的局部刚度来降低振动的幅值，从而达到抑制振动的效果。

如图21-63中所示，在原地板的基础上，增加两根X、Y方向的加强筋，筋的截面尺寸为宽10mm、高50mm，并模拟为梁单元，附加到原地板模型中。增加加强筋后，地板平均振动加速度和驾驶室内声压的变化如图21-64、图21-65所示。

从图中可知，驾驶室内声压约有7dB的降低。分析其主要原因，增加加强筋后，地板局部刚度提高，振动幅值降低，由振动所引起的声压也相应降低。但是，在89Hz位置的振动加速度虽然有约12dB的降幅，声压却几乎没有变化。这是因为此时的声压特性没有得到改善。声压分布如图21-66所示。

图21-63 加强筋

从本例中得知，单纯地通过增加加强筋，并没有在所关心的频率范围内得到声压的有效降低。当然，我们还可以继续采取措施，进一步降低结构表面的振动，来达到更好的声压降低效果，但是，由此而造成的重量、成本、尺寸的增加就得不偿失了。

图21-64 平均加速度的对比

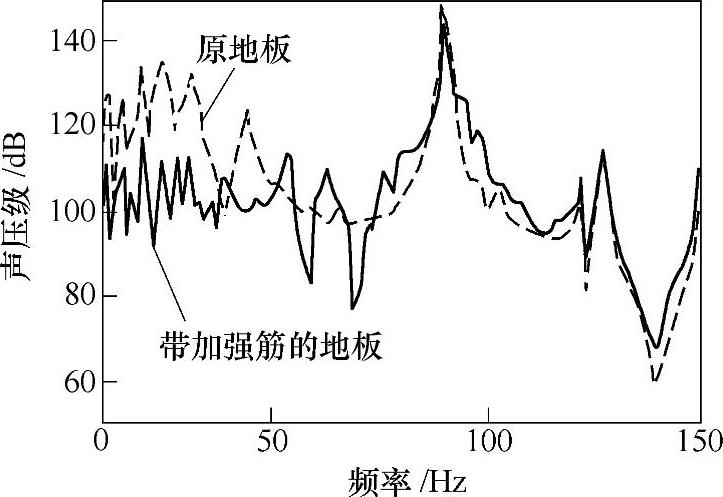
图21-65 声压的对比

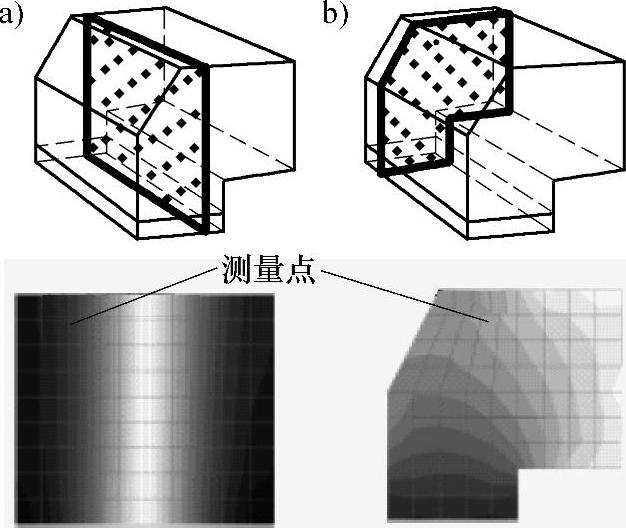
图21-66 声压分布（增加加强筋后）

（3）板件的曲面形状设计 为了更进一步降低驾驶室内的噪声，除了前述的增加加强筋以外，还应该寻找更为有效的优化方法。本例中，使用了MSC/NASTRANl软件的形状优化模块，通过对结构板件的形状优化，来达到振动、噪声的最佳改善目的。

以板件的曲面形状设计为着眼点。在板件的各种形状中，在两个方向上有曲率的曲面板通常要比平面板有更好的力学性能，而我们在实际设计上也常常会选择曲面形状。但是，不同的曲面形状其力学性能是不同的。在本例中，选择最有效果的减振降噪的曲面形状，是我们的目的。

通常使用B-spline函数来描述曲面形状。在函数中，使用参数ϕ、θ来表示曲面上点的坐标

以ϕ、θ为变量，就可以描述B-spline的积

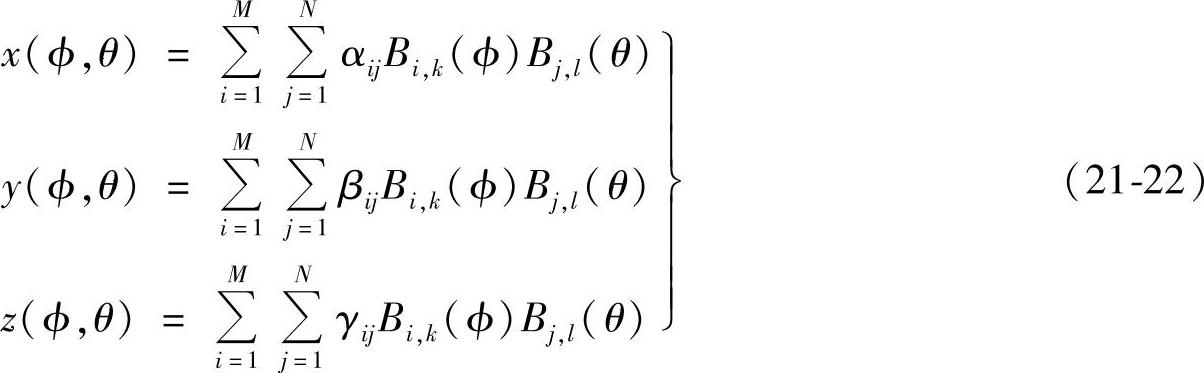
式中，B_i，k（ϕ），B_i，l（θ）分别是（k-1）、（l-1）次的B-spline；α_ij、β_ij、γ_ij是求解由包含控制点在内的所有点的坐标值构成的组合方程的常数。另外，M、N分别是1条ϕ曲线、θ曲线上数据点的个数。在本例中，k=l=4，M=N=5。

图21-67所示为作为研究对象的地板，及其上的点。地板的形状关于Y轴对称，共有25个带标记的点，其中，四周的16个△标记点固定，内部的6个●标记点为控制点，3个○标记点为对称点。以6个控制点的Z向坐标（z₁～z₆）为设计变量，在正向0～50mm范围内变化。而相应的对地板的FEM模型仅对控制点的Z向坐标加以更新。

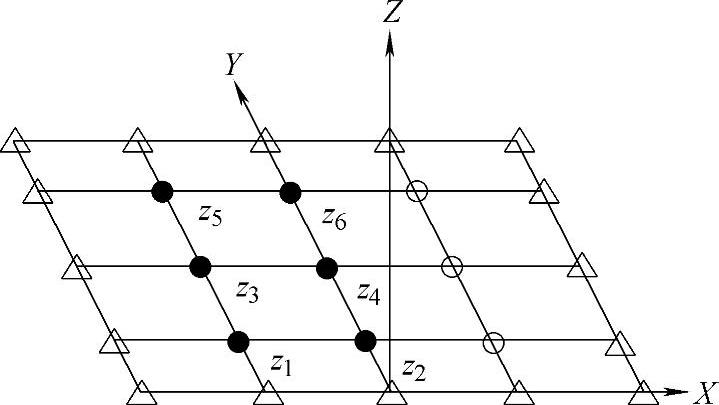
图21-67 地板及数据点

在进行优化分析时，如果想通过设计变量的变更来得到多组曲面形状，就不希望局部的变更影响到全体的形状。使用B-spline时，由于数据点坐标的变更对形状的影响是局部的，本次分析中假定FEM模型的网格变形对分析结果的精度没有影响。

（4）优化计算

设定150Hz以内的声压测量点的平均声压为目标函数，进行地板件的曲面形状优化分析。在开始分析前，需要进行一些变量设置。在6个设计变量中，z₁和z₂以5mm为刻度，在0～50mm范围内变化，其他的4个变量取一定值0。对每一个方案进行计算，结果如图21-68所示。

图21-68 z₁和z₂为变量时的平均声压

从计算结果可知，当有2个设计变量时，计算结果曲线上出现了多个响应峰值。如果再进一步增加变量的个数，可以预见结果的复杂性。

为了更快地找到最佳方案，如果不限定适当的变量范围，按照通常的数学方法会很难找到最佳结果。因此，本文中采用了遗传算法（GA）。遗传算法（GA）是一种高效、并行、全局搜索的方法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解。遗传算法操作使用适者生存的原则，在潜在的解决方案种群中逐次产生一个近似最优的方案。

遗传算法的原理：首先将问题求解表示成基因型（如常用的二进制和浮点型编码串），从中选取适应环境的个体，淘汰不好的个体，把保留下来的个体复制再生，通过交叉、变异等遗传算子产生一新染色体群。依据各种收敛条件，从新老群体中选出适应环境的个体，一代一代不断进步，最后收敛到适应环境个体上，求得问题最优解。其中再生的过程是将个体编码串按照它们的适应度通过一定的规则和方法进行选择。从当前种群中选出生命力强的染色体，组成交叉操作的父代种群；而交叉变异则让父代种群中的染色体，以选择概率P_C进行交叉操作，以变异概率P_M进行变异操作，产生子代种群。这可满足进化论中种群多样性的原则，更有利于种群更优个体产生。每经过这样的一次遗传算法过程，优化问题的解便朝着最优解方向前进一步。随着再生、交叉和变异操作的不断进行，问题将最终获得全局最优解。

根据以上说明，利用NASTRAN软件进行结构流体耦合分析，对曲面形状进行参数化设计，根据GA法生成计算程序，开始声压测量点平均声压级的最小化的优化分析。图21-69所示为计算流程，分析结果的相关输出文件，都是在程序上自动更新的。

图21-69 分析流程

（5）优化结果 图21-70所示为优化分析结果，其中显示了前10次的计算履历。横坐标为评价次数内的评价结果中的最佳值。对于这个优化结果，可能的设计变量的不同组合将达到2.8×10¹⁴个。

图21-71为优化后的地板曲面形状，图21-72为优化前后的声压结果对比。在关心的频率范围内，平均声压值比优化前大约降低了21dB。特别是在低频和驾驶室内声腔共振模态附近，声压有更大的降幅。相应的平均振动加速度如图21-73所示。

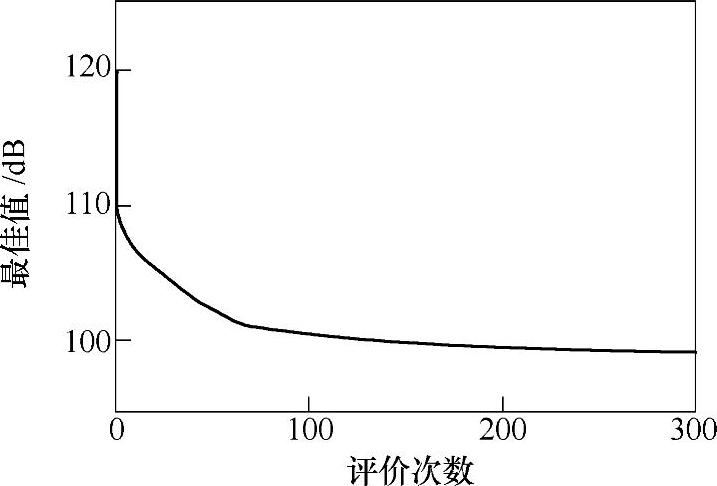
图21-70 计算过程履历

图21-71 优化后的地板曲面形状

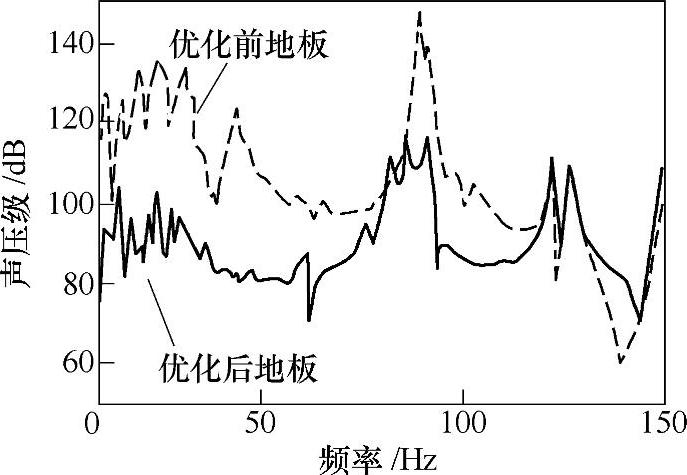
图21-72 优化前后声压对比

图21-73 平均振动加速度对比

地板采用曲面形状后，刚度增加。在低频范围内平均振动加速度有大幅度的降低，在声腔共振模态附近约有5dB的降幅，而与之对应的声压却有31dB的降幅。也就是说，声音传递特性的影响是这个声压峰值降低的主要原因。图21-74所示为采取优化方案后驾驶室内声压的分布。由图中可以看出，声压节点离测量点的距离更近了。

图21-74 声压分布（结构优化后）

从以上分析可知，优化分析中得到的结构形状，使低频范围内的板件振动幅值得到了有效控制。另外，驾驶室内声腔共振模态的节点位置也有所变化，在常用的频率范围内全体的声压级别得到了大幅度的降低。而此时，设计变量的最大位移变化只是板件宽度的5%，仅仅通过这一有限的更改，就达到了大幅度降低声压的目的。