汽车NVH技术：转向盘摆振与车轮陀螺耦合的影响

可以将转向盘摆振看成是车轴和车轮耦合运动的结果。图20-9中各符号的意义为：

I₀：车轮转动惯性矩。

I₁：围绕主销的车轮惯性矩。

I_e：前车轴惯性矩在通过车轴中点，且与车辆前进方向平行的水平轴上的当量惯性矩。

2πn：车轮角速度。

2πnI₀：车轮转动动量。

车轮转动惯量在承受颤振角速度作用下，就向旋转中的陀螺一样，即使其轴线水平，只要有一端支撑，陀螺的轴线依然可以缓慢地围绕垂直轴运动，这种运动可用来表示。

如图20-9所示，相互面对的左右车轮分别产生摆角θ₁和θ₂，这就是车轮无规则跳动的摆角。相对于跳动角θ₂的复原力矩，由于拉杆弹力c_e的作用，首先可以被看成等于c_el²_eθ，接下来再考虑到左右跳动角并不相等，必须考虑到转向垂臂（Pitman arm）弹性力c_s的影响。所以，第二个可以考虑的结果是，可以将因此引起的复原力矩看成等于c_sl²_s（θ₁-θ₂）。

图20-9 转向盘摆振与陀螺作用的耦合

此外，由于轮胎胎面的摩擦力直接作用在车轮上，在这个摩擦力的作用下，将引起复原力矩μθ₁。与μ有关的复原力矩系数中，存在两种成分：其一是与车轮转速成2次方关系的项，另一个是与转速无关的项。也就是：

μ=μ₀+μ₁（2πn）2（20-15）

这样，对于左侧车轮来说，其运动方程式为

对于右侧车轮来说，由于没有拉杆的弹性影响，下述的运动方程式成立。

如上所述，车轮跳动引起振动，振动又引起了陀螺作用力矩，以及轮胎与悬架的复原力矩，两种作用力矩组成了相对于车轴的复原力矩。因而，其运动方程可由下式表达。

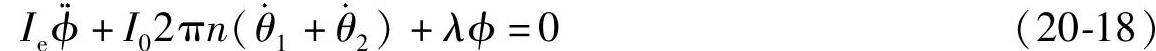
其中，λ=c₁a²+c₂s²，c₁和c₂分别是悬架和轮胎的弹性系数。此外，s和a如图20-9所示，分别表示为，两车轮之间的轮距和左右悬架弹簧的中心距离。

若假设连杆和拉臂的刚度相当高，则有c_s=0，c₁=0。又假设θ₁=θ₂=θ，则式（20-16）和式（20-17）将成为同一形式，结果变成如下两个运动方程式。也就是说，相对于转向机构的振动，，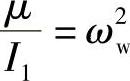

相对于车轴的振动，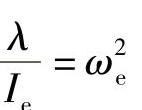

为了求解上式，设陀螺作用有90°相位差，则有下式。

θ=θ₀cosωt及ϕ=ϕ₀sinωt将两个方程式组合在一起，则有

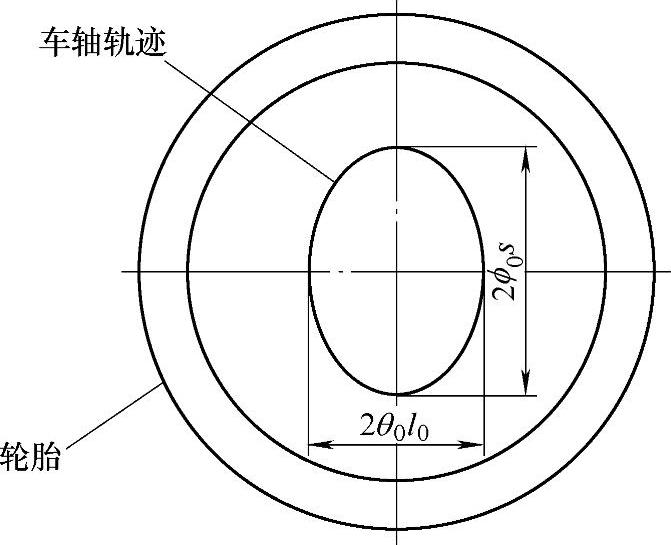
图20-10 车轮运动轨迹

因此，车轴中心的轨迹为椭圆。假设，l₀为主销到车轮中心的距离，s为车辙间距，如图20-10所示，这个椭圆的长轴和短轴分别为2ϕ₀s和2θ₀l₀。

接下来，将式（20-21）的关系代入到式（20-19）和式（20-20）中，可以获得如下条件。

将上式中的θ₀和ϕ₀消去，则可以得到下式。

上式的根分别为ω₁²和ω₂²，共计两项，通常是实数根，并且都取正值。(www.xing528.com)

当然，只要车轮不旋转，就不会产生陀螺作用。若此时车轮依然产生颤振和无规则跳动，假设其圆周振动频率分别为ω_w，ω_e，由于此时2πn为0，将n=0代入到式（20-19）和式（20-20）中，可以得到下式。

上述方程式的解如下所示。

这时，由式（20-15）可知，μ=μ₀。

只要车轮不旋转，式（20-23）中的ω就不应该等于ω_w和ω_e。实际上，由于在车轮旋转过程中承受陀螺作用，ω值也和ω_w与ω_e很相近，尽管相近，依然会多少有一些差别。假设，，将这些假设值代入到式（20-23）中，经过换算，可以得到下式。

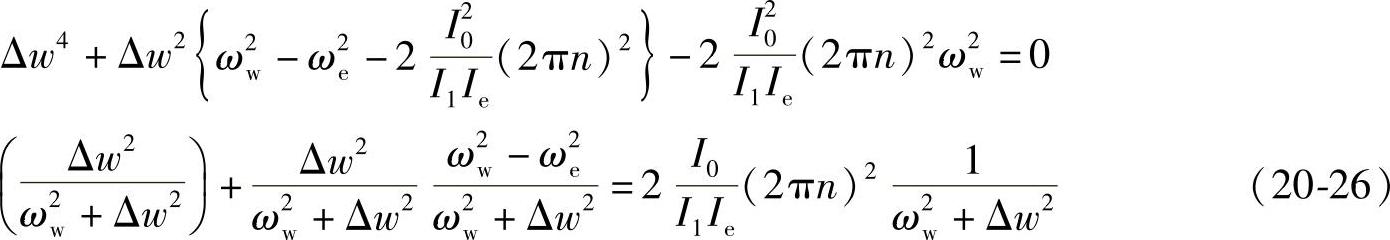
上式左边第1项和第2项相比小得多，可以省略掉，由此可以推导出下式。

同样方法，可以推导出下式。

将上述结果汇总成下式。

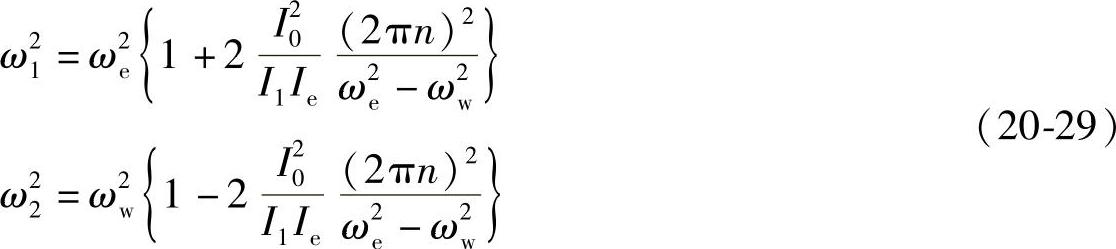
由上述结果可知，假设这种耦合振动的频率较高时设为ω₁，频率较低时设为ω₂，在耦合振动频率较高时，ω₁比车轮没有旋转的颤振频率ω_e还大。耦合振动频率较低时，ω₂比车轮的无规则跳动频率ω_w还低。

下面再讨论一下摆动角比率。由式（20-22）可知，

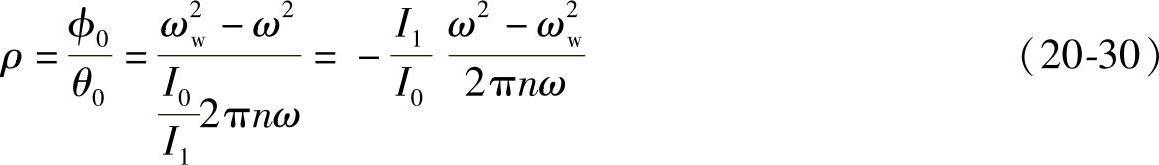
假设，上式中ω=ω_e，这相当于出现车轮颤振，则有

同样，

在该式中，若ω=ω_w，这相当于出现了车轮无规则跳动，则有

由上述结果可知，ρ和ρ′经常符号相反。

下面再讨论一下强迫振动。

对于强迫振动，只要在式（20-1）、式（20-2）的右边，加入强迫振动的强制转矩项即可。如上所述，所加的强制转矩周期（频率），必然和上述某一个耦合自激振动周期（频率）相等，因而引起共振，产生明显的振动感觉。

现以一个特殊状态为例，例如假设ω_e=ω_w。可由式（20-23）得到下式。

其中，为求解振幅比，对于车轮的颤振，将式（20-34）的关系代入到式（20-31）中，可得

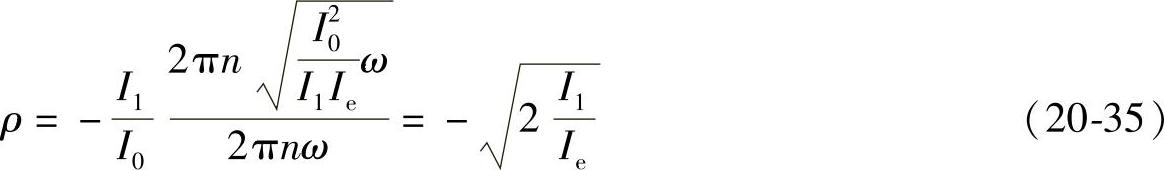
对于车轮无规则跳动，可将式（20-34）的关系代入到式（20-33）中，可得

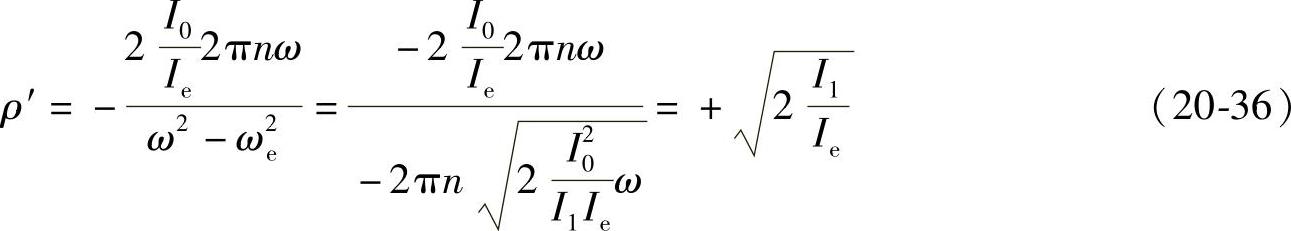
对于像这种随车辆行驶速度而产生的强制外力，应当用车轮转速的周期来观察更为妥当。因而，用式（20-29）求得的两个圆周振动频率ω₁和ω₂除以2π求得相对应的转速，若车辆前轮转速和这个转速一致时，将引起共振。