自激振动导致的转向盘摆振|汽车NVH综合技术

引起转向盘摆振的另一个主要原因是自激振动。自激振动是运动自身产生了使振动持续下去的周期激振力，所以，只要将运动停下来，这种周期激振力也自然地会消除掉。与此相反，强迫振动则不然，在强迫振动发生之前固然存在强迫激振力，有时，即使在强迫振动消除之后，强迫激振力也可能依然存在。这是和自激振动最大的差别。

自激振动力不断作用使振幅逐渐增大，这是自激振动的一个特征。有时自激作用还和吸振作用同时存在，结果使自激振动处于稳定的振动状态，这时的振动频率被称为固有频率。

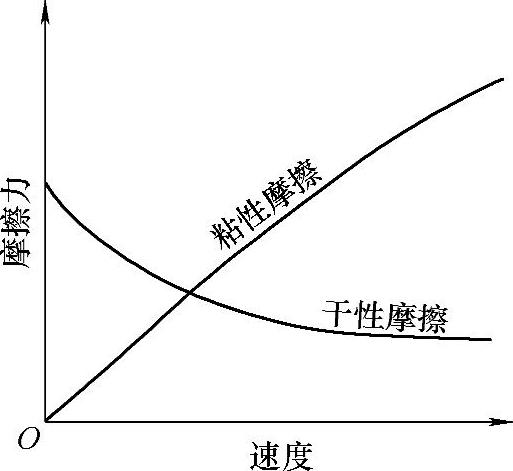
图20-4 摩擦力和速度的关系

引起自激振动的典型代表是摩擦力。以小提琴的琴弦和琴弓为例。在琴弦和琴弓之间的摩擦是典型的干摩擦，摩擦特性可参见图20-4，随着摩擦速度的升高，摩擦力出现降低的倾向。琴弓在某一时间内一直是单向运动，而琴弦则出现前后振动。琴弦和琴弓摩擦时，在琴弦振动的前半周期内，琴弦和琴弓的动作是一致的，后半周期两者运动方向相反。和琴弓的一个方向振动相比，琴弦的振动速度较小，导致在前半周期内，摩擦速度小，后半周期的摩擦速度变大。

这样，琴弓摩擦琴弦的摩擦力，前半周期要比后半周期大得多。这也就是琴弦能持续保持振动的原动力。琴弦和琴弓重复如下的自激振动模式。在琴弦和琴弓摩擦力的作用下，随着用力地把琴弦拉向琴弓运动方向，之后，琴弦产生的复原力超过了摩擦力，琴弦急剧地反弹回去。由于反弹的作用，使琴弦和琴弓之间的相对摩擦速度变大，摩擦力变小，琴弦一方面承受极小的吸振力，另一方面朝向相反方向，反弹回到极端位置。在极端位置附近，琴弦的振动速度近似等于0，摩擦力增大，再次出现用力将琴弦拉向琴弓方向的作用。

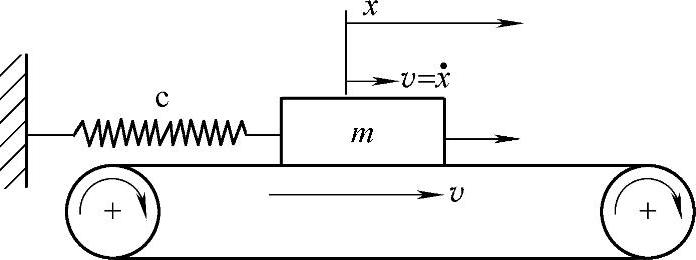
图20-5 自励振动模型

下面考虑一下图20-5的振动模型。设质量为m的物体位于平面上，处于容易滑动的状态，将其通过弹簧c连接到固定壁上。因为自激振动，以v₀速度拉动物体，物体将一边振动，一边被拉向外力方向。

假设物体初速度为v₀，则物体的运动方程式可由下式给出。

若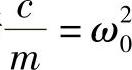，上式可改写成下式

可以用x=Acosω₀t+x₀形式得到上式之解。将上述之解代入式（20-2），则有

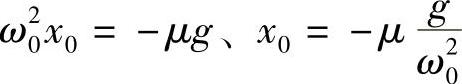
初始值，即ω₀t=0时有

x₀=A+x₀（20-3）半周期之后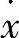，=0，这时可有ω₀t=π，则有

xπ=-A+x₀（20-4）

也就是说，物体的运动行程是从A+x₀点到-A+x₀，反复变化，两者之差为2A，这就是振动的振幅，振动中心为x₀，该位置和x=0位置相比，更靠近右侧。

以上的讨论条件是摩擦系数一定。一般而言，干摩擦的摩擦系数和摩擦速度有关，摩擦系数μ随摩擦速度增大而减小。

假设，摩擦速度v₀时的摩擦系数为μ₀，速度少许上升到v之后，摩擦系数为μ。

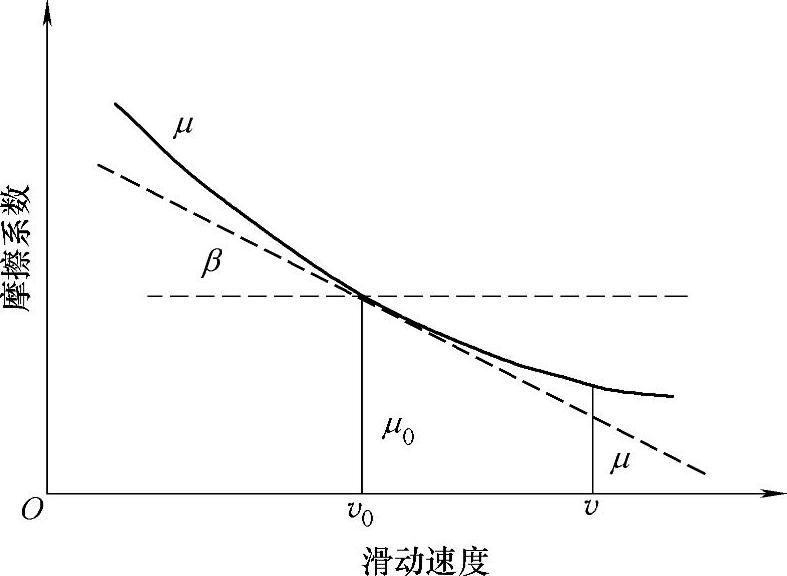
图20-6 摩擦系数的滑动速度特性

由图20-6可知，μ=μ₀-（v-v₀）tanβ。若物体的运动速度为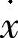，路面的滑动速度为v₀，则相对摩擦速度为两者之差，则有

将相对滑动速度带入到μ的计算式中，则有

(www.xing528.com)

将上述结果带入到式（20-1）中，得到下式。

由于振动中心为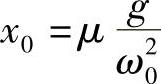，以运动中心作为原点，可将运动方程式改写成下式。

为了求解上式，。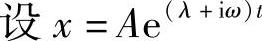

将这个假设值代入式（20-9）中，可以得到下式。

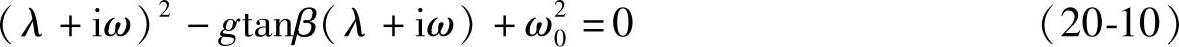
将上式分解成实部和虚部，分别求解，则有

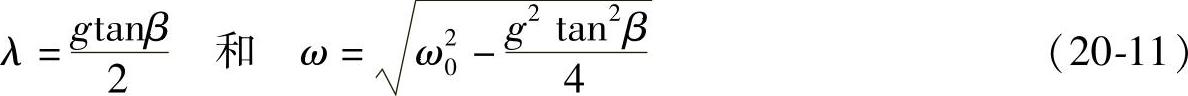
所以行程x的计算式如下式所示。

x=e^λt（Asinωt+Bcosωt）（20-12）

设初始条件t=0时，x=0，则有B=0，

x=Ae^λtsinωt（20-13）

由于摩擦系数曲线的斜率为负值，根据式（20-6），tanβ的值为正值。

从而，由式（20-11）获得λt≥0，即x呈变大趋势。然而随着振幅逐渐增大，由于周期保持不变，振动速度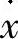最终要超过路面的滑动速度ν₀，这时，摩擦力作用方向将开始朝向相反方向，结果使运动方程式发生变化，如下式所示。

x=Ae^-λtsinωt（20-14）

随着时间的流逝，振幅开始逐渐变小（图20-7）。

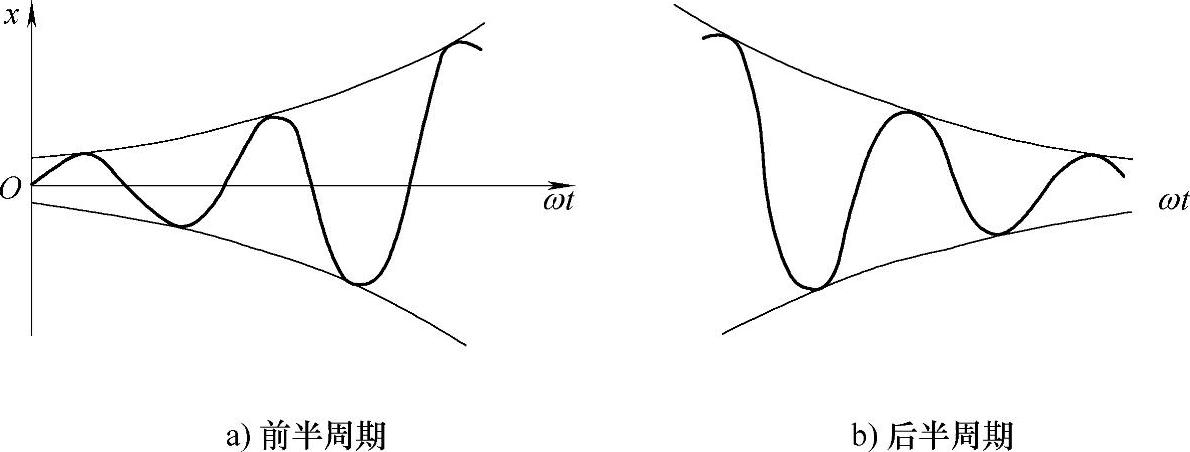
图20-7 物体动态

上述说明，也适用于车辆的转向盘摆振（图20-8）。

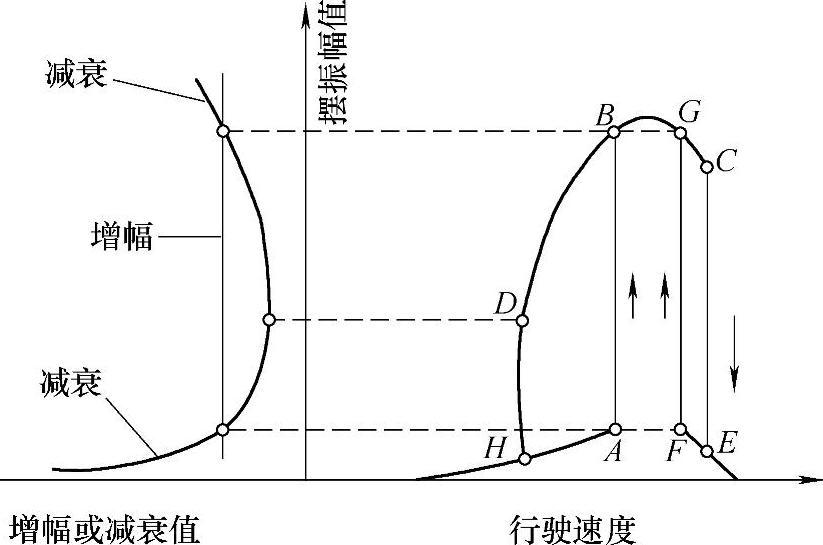
图20-8 转向盘摆振与车辆行驶速度的关系

车辆在行驶速度较低的区间内，阻尼力作用较大，因而，转向盘摆振的振幅也不太大。随着行驶速度提高到一定车速，阻尼作用发生变化，向相反方向改变，即变向到助长振幅增加的方向，导致振幅急剧增大。

然而，和行驶速度相比，滑动速度增长得更快，车速继续升高，阻尼作用将再次出现，使转向盘摆振的振幅变小。如图20-8所示，随着车速升高，转向盘摆振振幅将沿着曲线H—A—F—E变化。反之，当车速逐渐下降，转向盘摆振振幅将沿着曲线E—F—G—B—D—H变化。

由上述分析可以看出，因为前车轮的前束设置不当，使轮胎的胎面和路面之间产生大的摩擦阻抗，结果导致了转向盘摆振。由这样的思路，就可以理解轮胎摩擦力是转向盘摆振的起因。