汽车驱动轴系弯曲变形的能量和动能

驱动系统可以简化为图1--16所示的8自由度模型。

动力总成如图1--17所示，分为发动机本体和变速器两部分，分别以刚体模拟，二者之间用等价弯曲刚度单元连接，其前后端也都通过弹性单元支撑。传动轴的两端为单纯支撑，其重量集中在重心G₃处，如图16-18所示。后桥总成视为刚体，通过板簧连接到车身，并最终通过轮胎与地面接触。因此，板簧可以分为前半部分和后半部分，重量集中在各自的重心位置G₅、G₆处，系统的自由度包括重心G₁～G₆的上下方向运动和重心G₁、G₂、G₄的俯仰运动，发动机本体和变速器壳体之间的结合可以去除一个自由度，共计8个自由度。

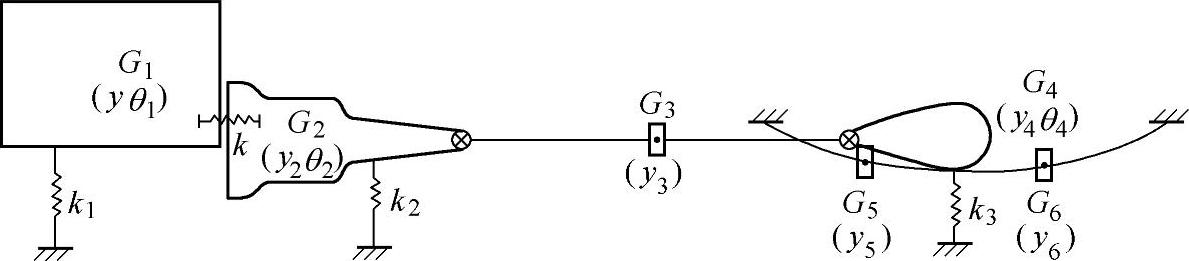
图16-16 驱动系统分析模型

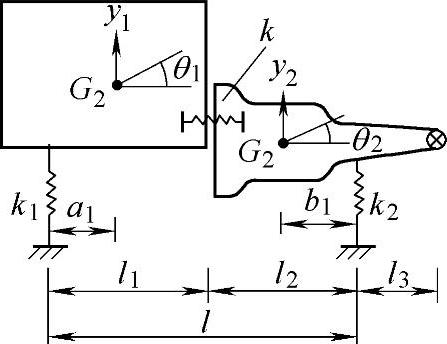
图16-17 动力总成模型

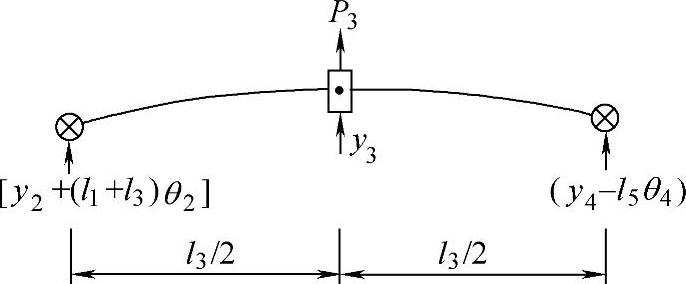
图16-18 传动轴计算模型

动力总成的变形能U_E和动能T_E可以用下式求得：

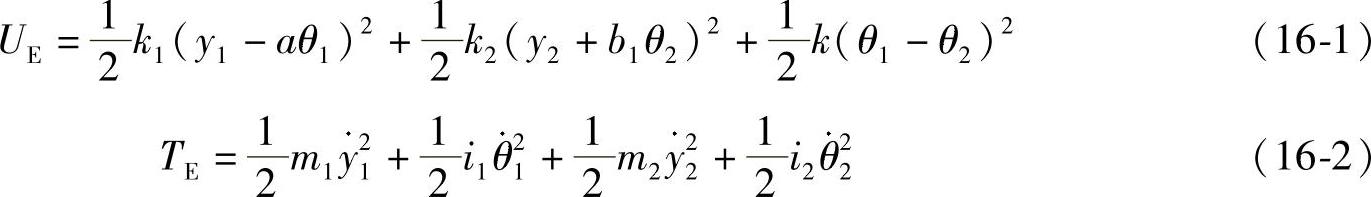
发动机本体和变速器壳体的结合条件如下式所示，据此可以去除一个自由度。

y₁+（l₁-a₁）θ₁=y₂-（l₂-b₁）θ₂（16-3）在传动轴的重心G₃处施加P₃外力，则传动轴的变形能可按式（16-4）求得。

重心G₃的位移为

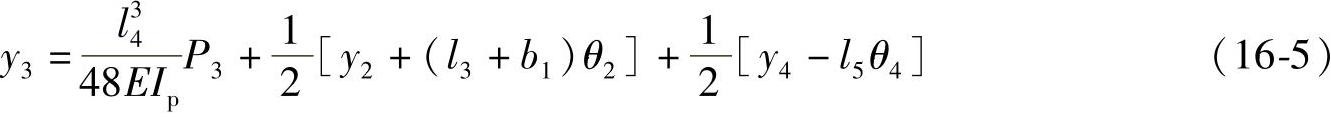
从式（16-4）、式（16-5）可将P₃消去，传动轴的变形能变为

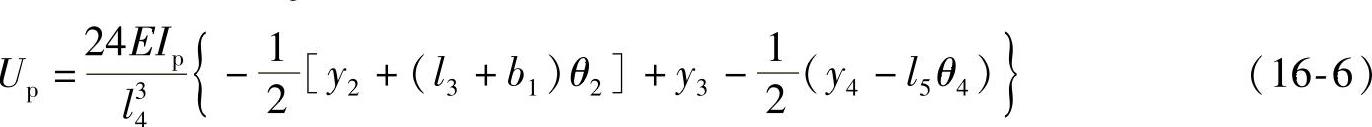
另外，传动轴的动能T_p可按下式求出：

接下来，后桥总成、板簧、轮胎的变形能和动能也可以求出。如图16-19所示，在重心G₄、G5、G6处施加外力P₄、P₅、P₆，重心G₄处施加力矩M₄，将板簧如图16-20所示展开分析，两根板簧的变形能U_L则为

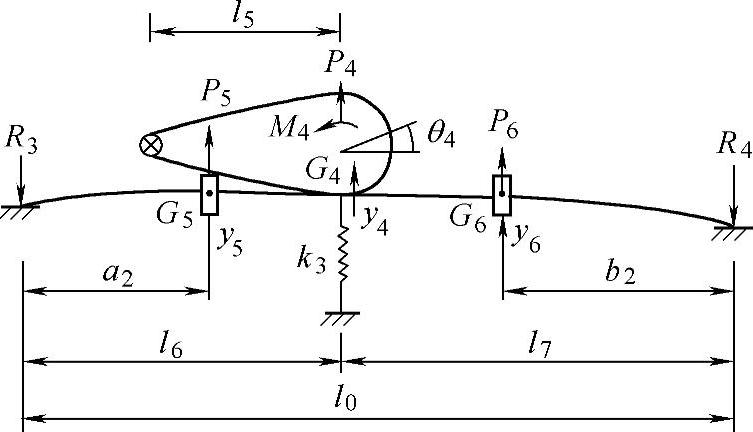
图16-19 后桥总成分析模型

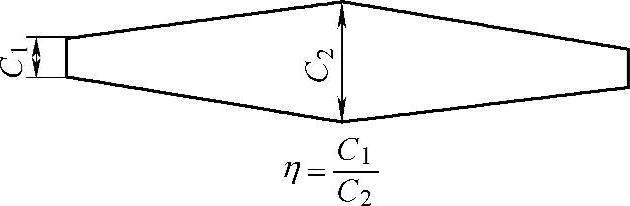
图16-20 板簧展开模型

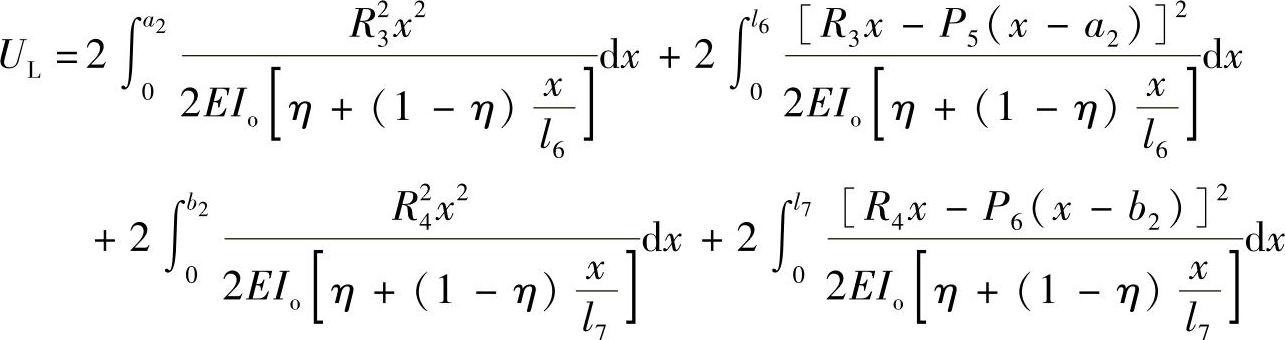(https://www.xing528.com)

也可以表达为

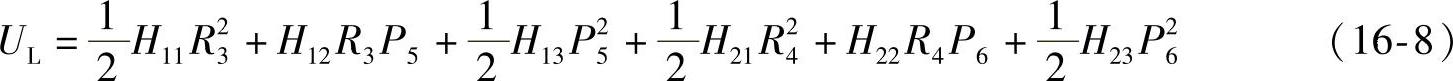
式中，R₃、R₄为板簧的前后支持反力。

式（16-9）中，

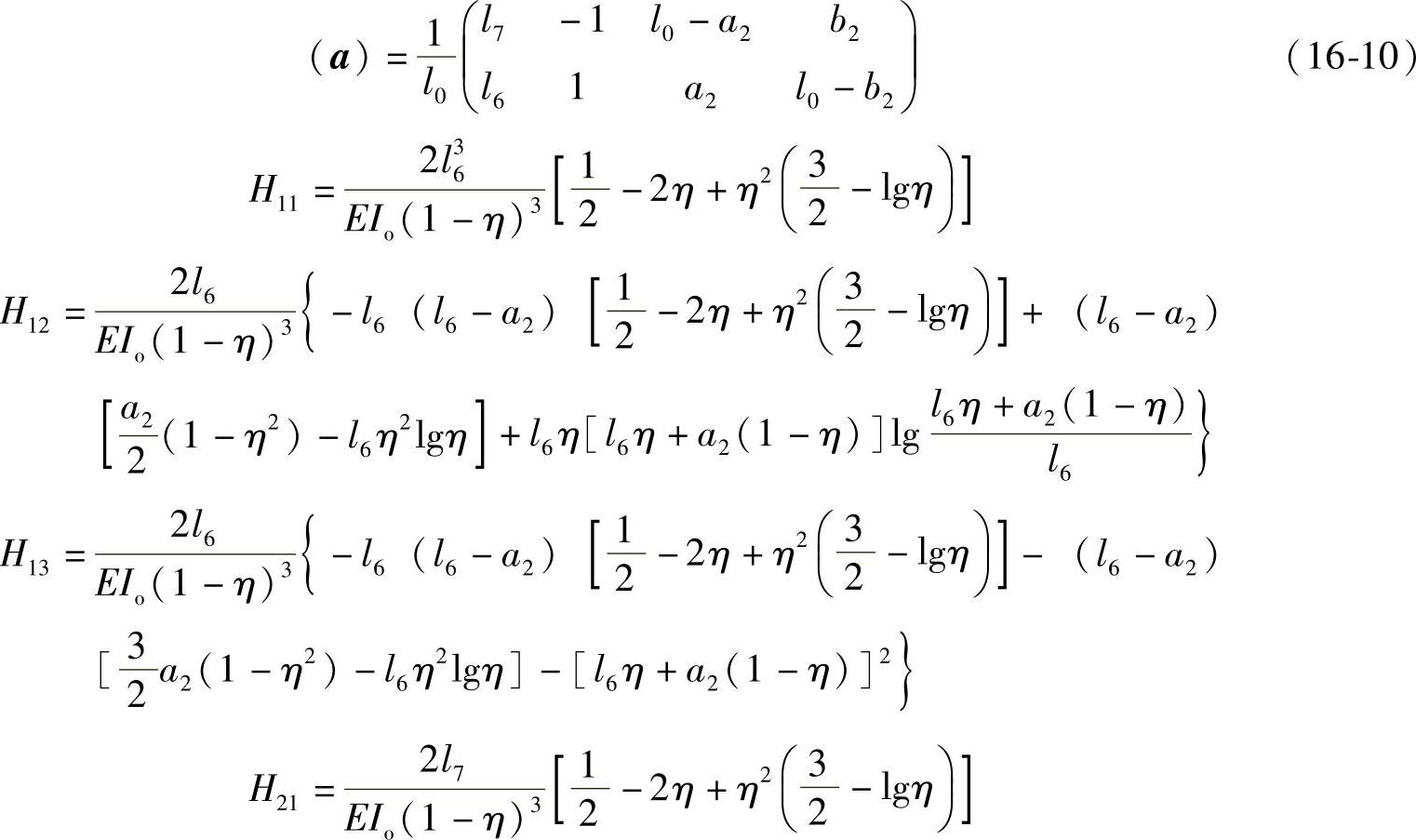
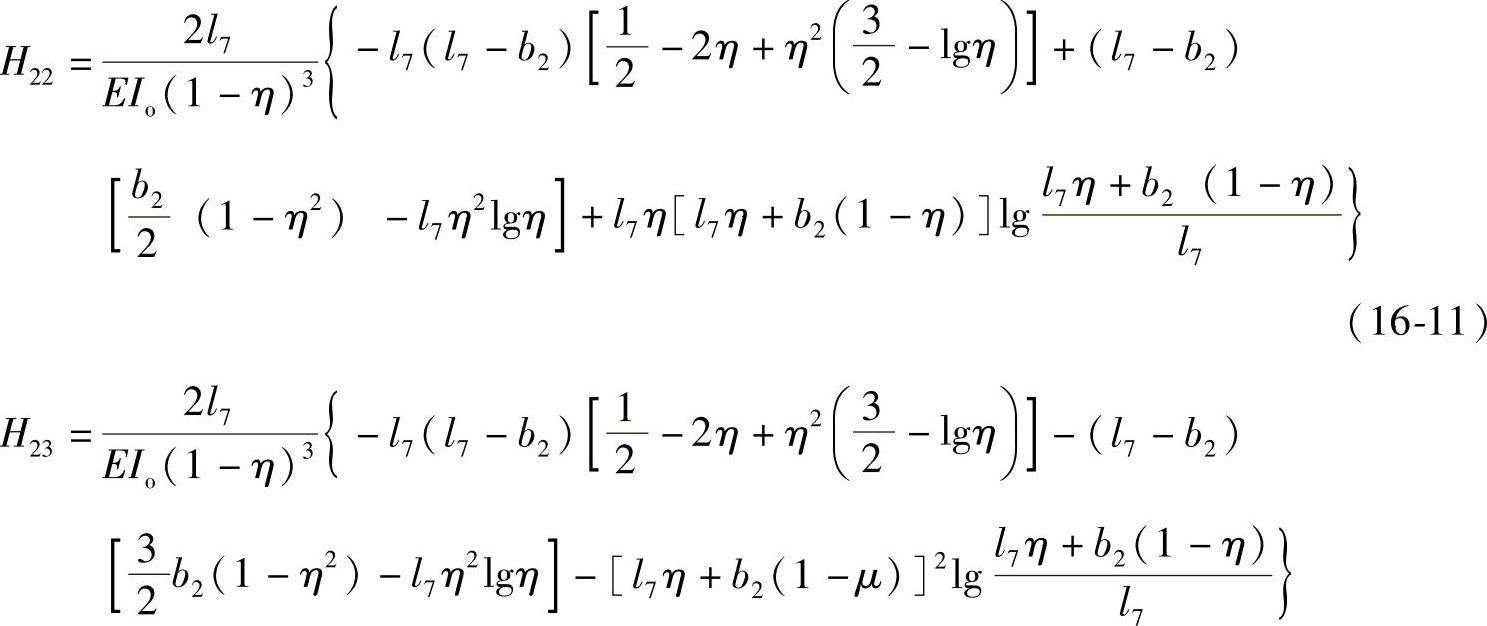
此时，对重心G₄、G₅、G₆位移及重心G₄角位移按Castigliano定理整理后得

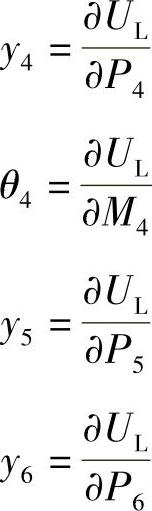
也可以表达为

式中，

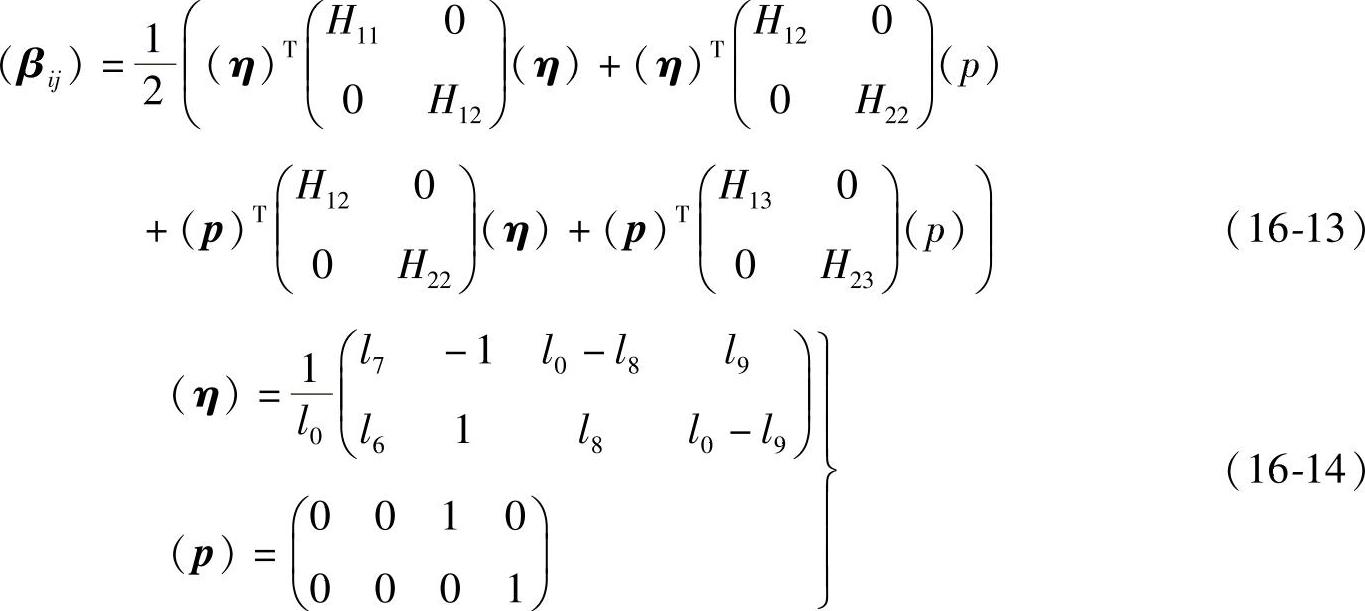
（η）T、（p）T为（η）、（p）的翻转矩阵。

从式（16-12）可以知道P₄、P₅、P₆、M₄有如下的关系：

其中（δ_ij）、（β_ij）互为逆矩阵，即

（δ_ij）=（β_ij）-1（16-16）从以上的结果可以推出，两根板簧的变形能U_L可以用位移y₄ y₅ y₆ θ₄表达：

U_L=U_L（y₄，y₅，y6，θ4）（16-17）而两个轮胎的变形能可以表达为

U_T=k₃y²₄（16-18）后桥总成、板簧的动能T_L可以用下式求得：

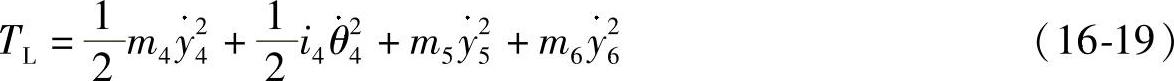
基于以上分析结果，驱动系统整体的弯曲变形能U和动能T可表达为