汽车NVH技术：解析制动啸叫现象

1.分析模型

众所周知，引起自激振动的摩擦特性是与速度相关的，但是关于摩擦系数一定时耦合系统的自激振动方面的报告却很少。本文考虑模拟制动系统的简单的2自由度模型，根据复数模态分析，首先对耦合系统的自激振动进行定性分析。其次在自激系统上使用动态减振器，对减振效果进行论证。

图11-6为分析用的模型。不考虑减衰时的运动方程式见式（11-2）。式中的第2项为刚度行列式，其非对角项为非对称数值。对该式进行复数固有值分析，式（11-3）为解的形式。

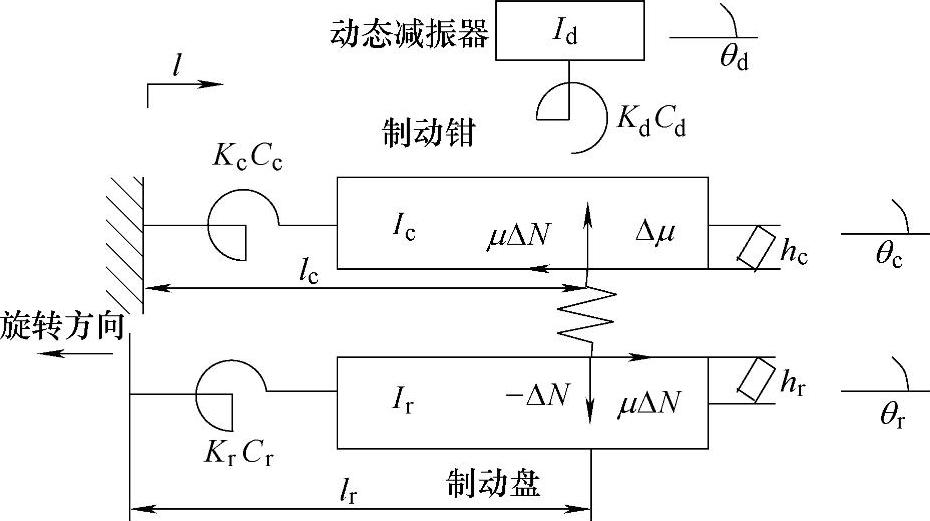
图11-6 2自由度分析模型

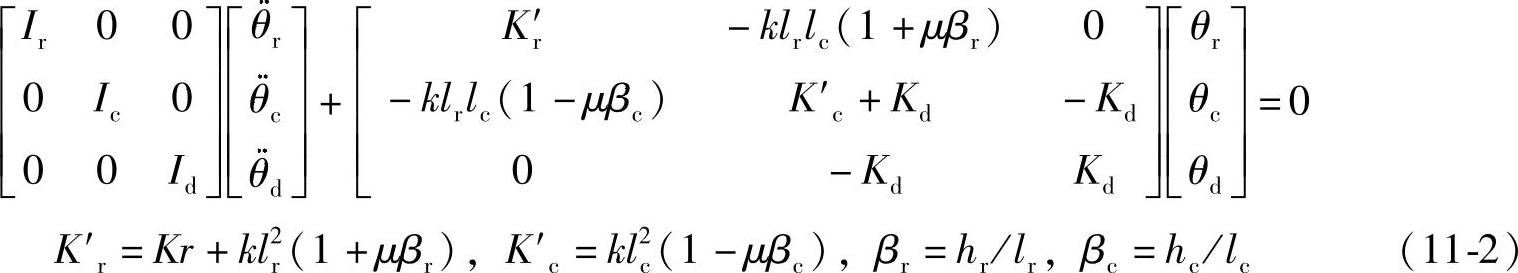
复数固有值

λ=λ_R+j2πf_n（11-3）

式中，λ_R为复数固有值的实部（1/s）；f_n为耦合固有振动频率（Hz）；。

复数固有值的实部λ_R为负数时，振动是减衰的，正数时是发散的，此时的耦合振动频率f_n与啸叫频率相对应。另外，λ_R的值越大，则振动能量的发散也越大，因此，可以用λ_R作为啸叫的评价指标（下面称其为啸叫容易度指数）。

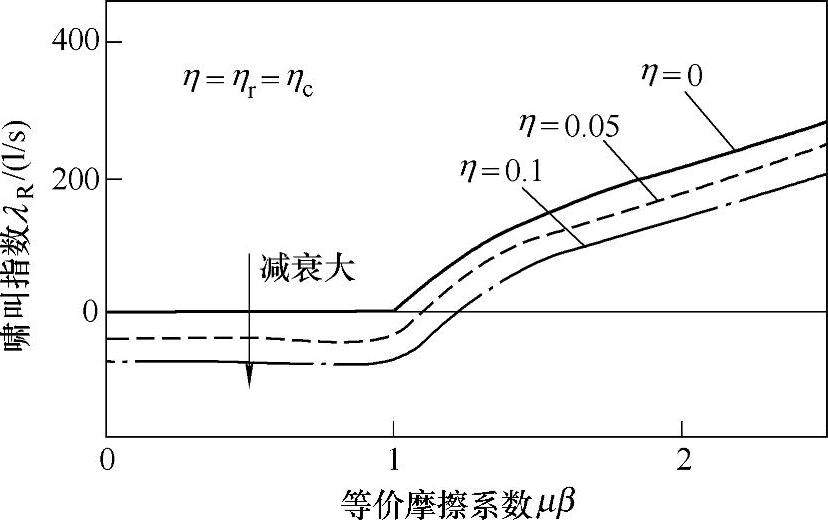
图11-7 减衰的影响

①制动盘、制动钳构成的2自由度模型。如图11-7所示，横坐标为考虑形状的等价摩擦系数μβ，纵坐标为λ_R，图中显示的是当μβ增加时，不同减衰指数C_r、C_c时的λ_R变化情况。

损失系数

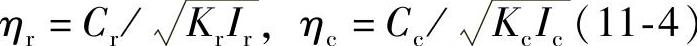
利用上式进行整理后，当η增加时如果λ_R>0，则μβ的值也是增加的。也就是说系统的减衰对啸叫是起抑制作用的。当μβ_r，c=±2.0时，制动盘与制动钳的固有模态的比f_r/f_c和λ_R的关系如图11-8所示。从图中可知，当制动盘和制动钳的旋转中心偏左（μβ_r，c=+2.0）时，由于f_r/f_c>1，存在啸叫发生的领域，并且当惯性矩的比I_r/I_c增加时，该领域扩大。相反，当制动盘和制动钳的旋转中心偏右（μβ_r，c=-2.0）时，由于f_r/f_c＜1，存在啸叫发生的领域，并且当惯性矩的比I_r/I_c增加时，该领域有缩小的倾向。根据以上分析，可以知道制动盘和制动钳的模态对啸叫是有影响的。

虽然过去多是以固有值之比来讨论啸叫问题，但从以上分析可以知道，模态及惯性矩的比也有着相当大的影响。

②追加动态减振器。如图11-9所示，对动态减振器的固有振动频率f_d和啸叫容易度指数的关系进行了研究。图中的箭头表示耦合后的固有振动频率，η_d可以按照下式求得：

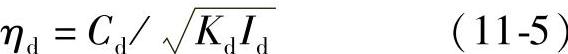
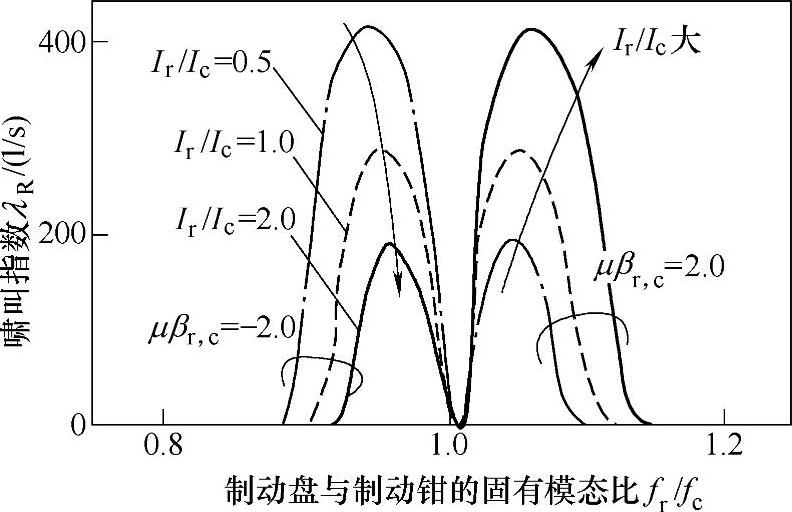
图11-8 固有频率的影响

把f_d设定为比耦合固有振动频率f_n高5%左右时能得到最佳的改善效果。另外，与强制振动不同的是自激振动的减衰较小时制振效果更好。而当动态减振器的惯性矩较大时，λ_R≤0的频率范围更宽。

基于以上分析结果，可以得到以下的改进方向和注意点：

●制动盘或者制动钳的减衰尽量大。

●动态减振器的固有振动频率f_d要比耦合固有振动频率f_n稍高一些，减衰稍小一些。

●不能仅仅以固有值的比来分析啸叫问题，还要考虑振动模态和惯性矩之比。

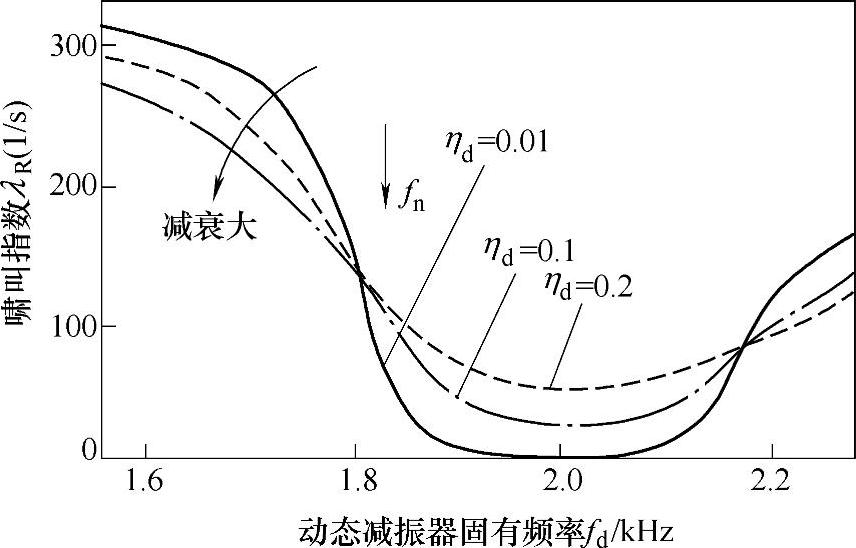
图11-9 减衰的影响

2.FEM分析

通过FEM分析可以为解决制动啸叫问题提供方向性的建议。但是，由于制动系统结构复杂，具体的结构状态很难用FEM模型真实地模拟出来。(www.xing528.com)

当前，有限元法是忠实反映制动系统动态特性（刚度、固有频率）的最为有效的方法。因此，为了定量掌握各个参数与制动啸叫问题的关系，本文介绍一种新近开发的根据FEM方法来求解制动系统的固有模态。

（1）FEM法复数固有频率分析 为了能够用FEM方法表现线性的摩擦振动，必须进行复数固有模态分析，而在这之前需要解决以下几个事项：

①利用FEM方法体现摩擦力，现存的单元不适用于非对称行列式。

②计算的实用性，分析用的模型如果超过50000自由度，计算时间、内存消耗巨大。

对于第①项的解决方法，如同式（11-6）中的第3项，在结构全体刚度矩阵中追加式（11-7）中的接触刚度矩阵。产生的摩擦力等于制动盘面垂直方向的刚度矩阵乘以摩擦系数，这样就实现了制动盘和衬垫之间真实刚度矩阵的定义。

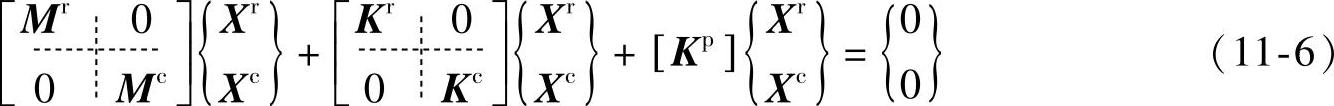
式中的K^p是定义制动盘和制动钳运动副之间接触的刚度矩阵：

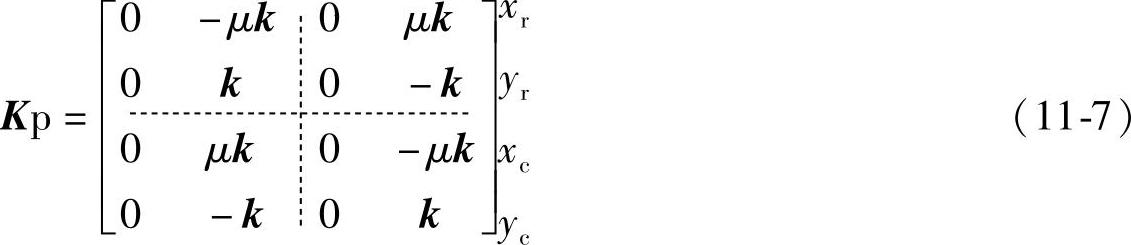
式中，x为摩擦力的发生方向；y为制动盘面的垂直方向；k为衬垫摩擦材料的制动盘面垂直方向的刚度矩阵。

对于第②项，导入部分结构合成法。对制动系统、制动钳系统分别进行模型变换，分析自由度缩小为原来的1/1000。使用超级计算机进行复数固有模态分析时需要几个小时，经过模型变换后，仅需要1min即可完成计算。

另外，随着现代电子技术的飞速发展，计算机的性能有了巨大的进步，软件方面也得到了快速的发展。即使不使用模型转换，利用高性能配置的计算机和软件，也可以在短时间内得到模态的解。

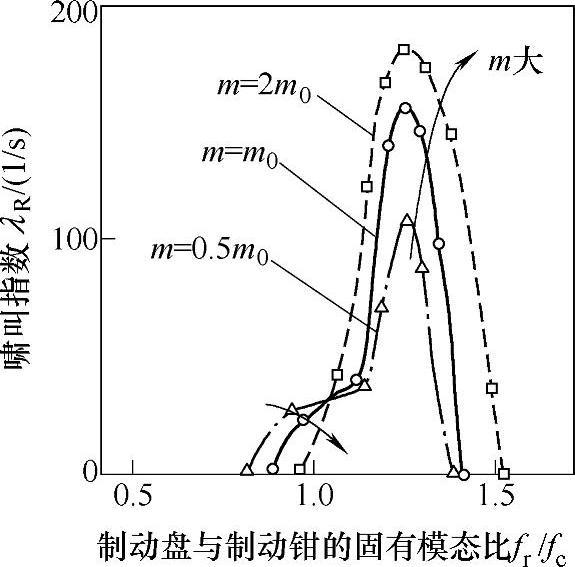
图11-10 动态减振器的影响

（2）计算结果 最初，制动钳的结构未进行任何变更，仅对制动盘的刚度、质量加以调整，对制动盘与制动钳固有频率的比值f_r/f_c与制动啸叫容易度指数λ_R之间的关系加以调查。需要关注的固有频率比，是制动钳的扭转模态和制动盘的3阶直径方向模态这二者之间的比值。

图11-10是仅变更制动盘的模态刚度以调整固有频率的比时，将制动盘的模态质量调整为2倍和0.5倍时的计算结果。

图11-11为制动系统各零部件的模态分布，以及与制动噪声之间的对应关系。其中比较典型的有制动蹄的扭转和弯曲模态、制动鼓的径向弯曲模态。图11-12为制动鼓的径向弯曲模态与制动噪声时间领域测试结果的对应关系。曲线中的峰值A或者谷值B与制动鼓的模态是对应的。

同计算模型的结果相同，FEM分析模型中也显示存在λ_R>0领域，在固有频率比为1.25附近存在峰值。另外，当制动盘的模态质量增减时λ_R的绝对值也有变化的倾向。计算模型的固有频率比以1.0为边界条件，因模态的不同，λ_R>0的领域分为两部分，而FEM模型却是在固有频率比0.8～1.4的范围内连续为正值。这是由于FEM模型在该范围内的固有值之比，造成前述的两个模态连续变化。总的来说，FEM模型与计算模型不同，它可以体现模态及质量比的变化倾向。图11-10的分析结果证明了当固有值比为1.0时，相对于模态质量的增减，λ_R绝对值的增加倾向具有明显的转折点。

其次，对动态减振器的效果进行详细的论证。

图11-13为将动态减振器安装在制动钳外拖臂一侧时的减振器固有值f_d和啸叫容易度指数λ_R之间的关系。图中箭头指的是未安装动态减振器时的啸叫频率f_n。

当动态减振器的质量为10g时，使λ_R<0的固有值领域几乎不存在。而当动态减振器的质量增加到30g时，λ_R<0的领域扩大到f_d=1.80～2.05kHz。

通过以上分析可以得到这样的结论：将动态减振器的固有值f_d设成高于未安装时的啸叫频率f_n，就能得到很好的制振效果。如果动态减振器的固有值f_d设成低于未安装时的啸叫频率f_n，就会出现啸叫容易度指数λ_R增加的领域，这一点需要特别注意。

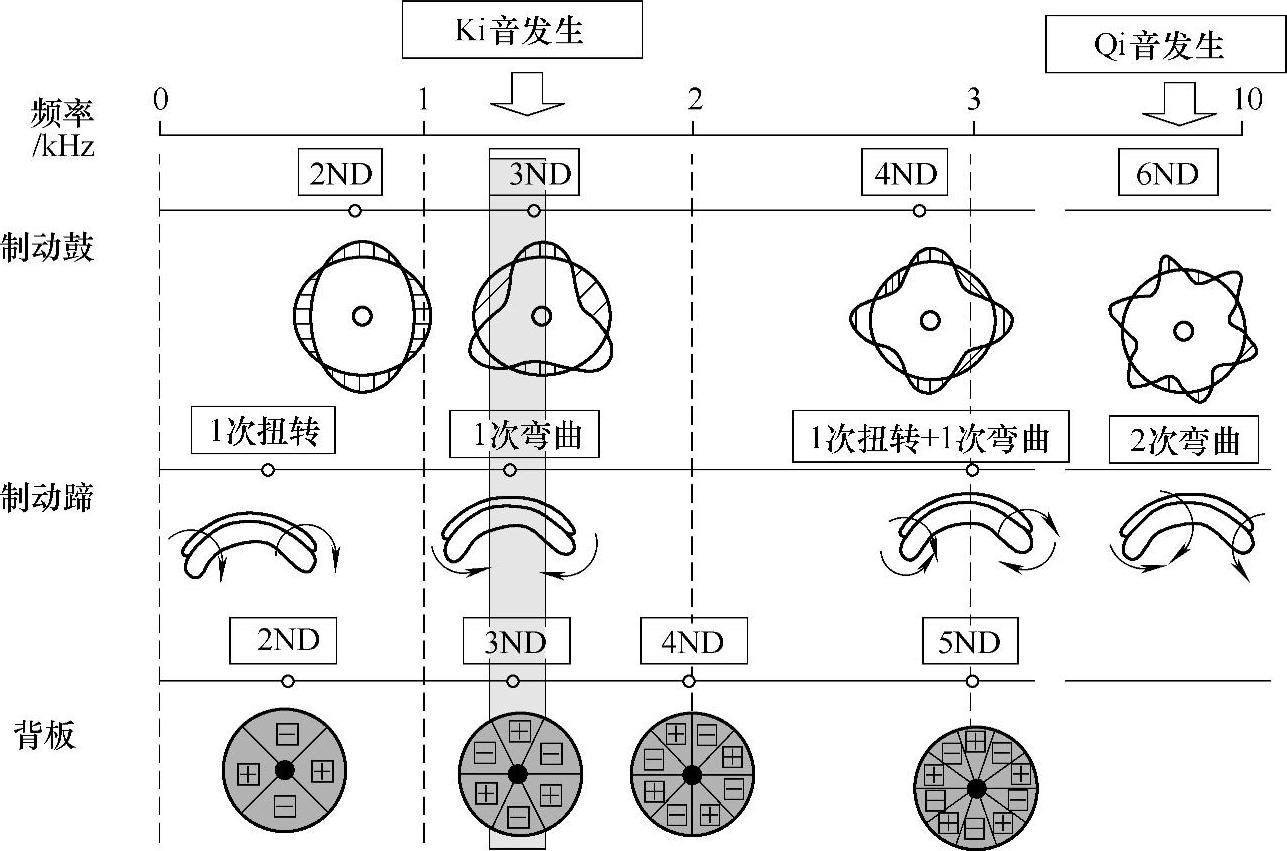
图11-11 制动系统模态分布

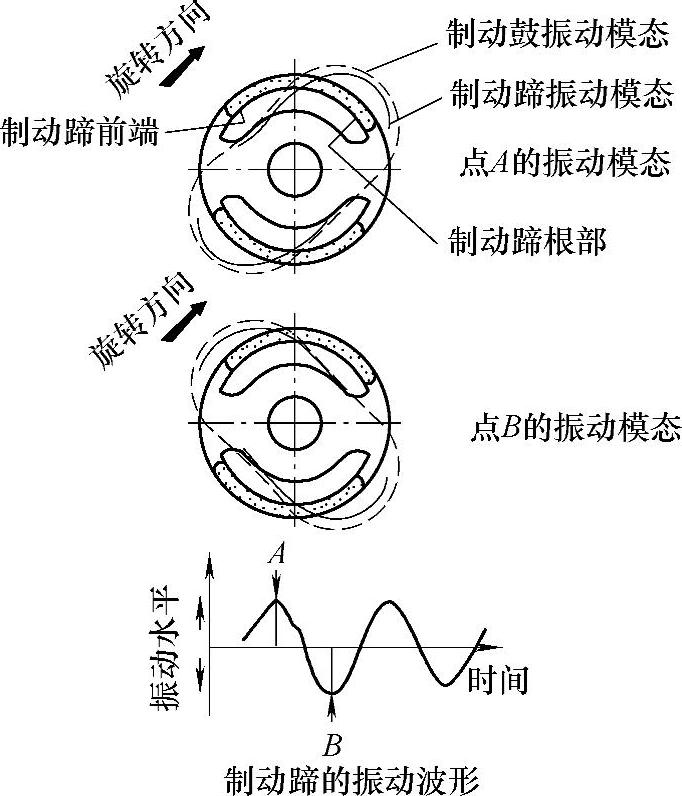
图11-12 制动鼓的径向弯曲模态

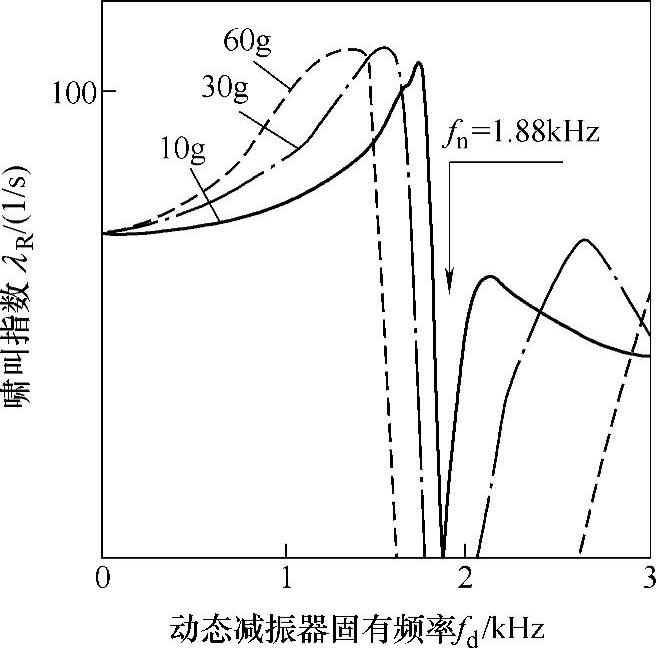
图11-13 动态减振器的效果

另外，和计算结果同样，动态减振器自身的减衰性能越小，则制振效果越好。这一点对于强迫振动来说，动态减振器的设计是完全不同的。