声音基础理论与解决方法

为了说明人是如何听到声音的，先介绍一下声音产生的基础理论，以便更好地理解与声音有关的各种现象及解决方法。

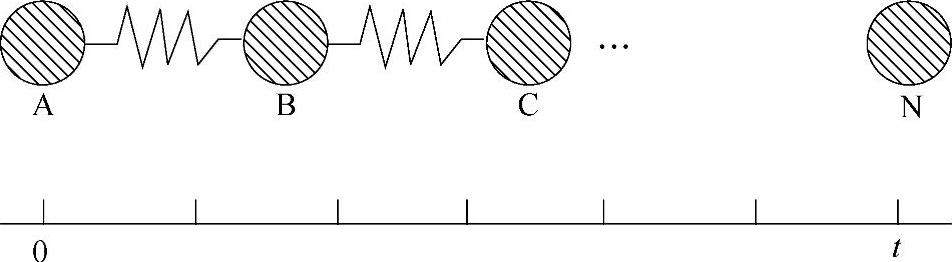
图1-1 运动的传递

为了说明声音在介质中传播的原理，以一个实体球和弹簧结合成的多质点系的运动来加以说明，如图1-1所示。球体在质量产生的惯性力、弹簧回复产生的弹力的作用下产生运动。当t=0时，球A受到外力，球A的运动经过弹簧向球B传递。球B的运动因惯性作用而相对于球A有一个延迟，接下来球B再向球C传递，同时伴随着时间的延迟。

以此类推，球A上所发生的运动以有限的速度向外传递。如果假设这个传播速度为c，经过时间t后传播的距离为ct。因此，距离初始端x处球处于平衡状态时其位移用下面的式子表示

a=f（ct-x）（1-1）

将上式作2次求导后可得

该式是表达具有任意形状的平面波的时间、空间经历变化的最简单的波动方程。下面结合具体的物理现象，对该式进一步加以展开讨论。

首先，声波在传递过程中，引起介质变动，造成介质的分布疏密不均。取出其中的一小块微小单元，讨论其所受到的外力。图1-2显示的是简易的一元模型，在实际应用中可以很容易地展开为三元模型。该微小单元上所受的外力可以用下式表达

式中的u称为粒子速度，用来代表微小单元的速度。上式是按照流体的运动所定义的具有严

密解的运动方程，通常可以作一些假定后加以简化。

1）密度的变化量相对其绝对值很小，所以假定ρ=ρ₀（正常状态下的密度）。

2）粒子速度u比音速小，故可以作如下简化

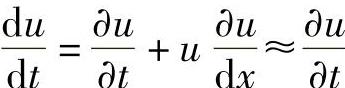
因此，式（1-3）可以转化为

这就是人们熟知的表示流体中动态平衡力的欧拉（Euler）公式。

其次，考虑流体运动的质量守恒法则。

如图1-2和图1-3所示，声波在行进时，仅有微小单元中存在的流体层ξ在移动。这个ξ即称为声波位移。

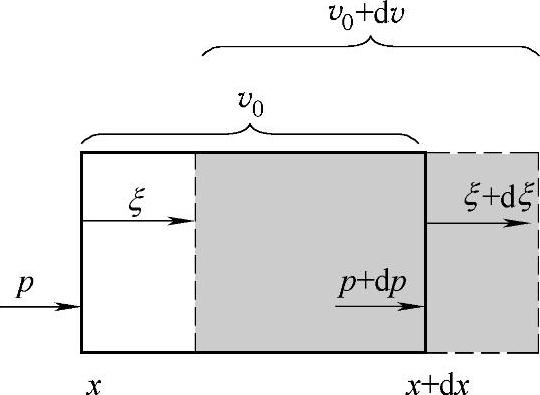
图1-2 声波运动分析模型

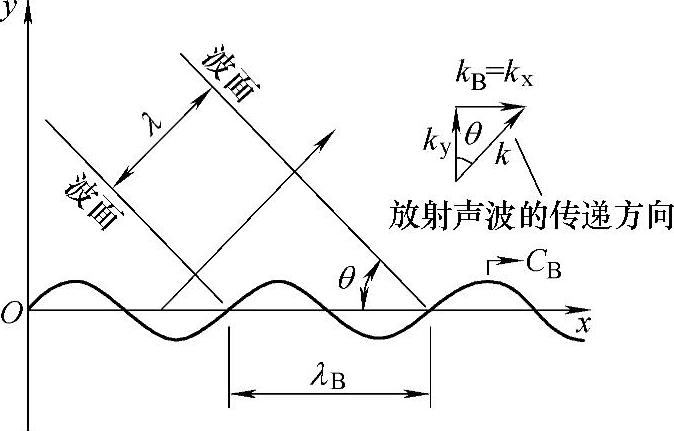
图1-3 声波传播示意图

这个移动量，在位置x+dx时为ξ+∂ξ/∂xdx。因此，该微小单元中，流入的质量为ρξdydz，流出的质量为ρ（ξ+∂ξ/∂xdx）dydz，其质量的变化量是与分析范围内的密度变化对应的

（ρ-ρ₀）dxdydz=-ρ∂ξ/∂xdxdydz

等式两边同时对时间t求导，且∂ξ/∂t=u，于是可得

把∂p/∂x=c²∂ρ/∂x（c为声速）导入式（1-4）、式（1-5）中，可得以下的波动方程

这就是平面波的波动方程式。该式的一般解可以表达为p=F（ct-x）+G（ct+x）。如果以角频率ω、波数（单位长度内所包含的声波数量，单位为m^-1或者cm^-1）k来表示正弦波，可以用下式表示，其中前者为行进波，后者为后退波。

同样，可以列出球面波、圆筒波的波动方程。

球面波：

圆筒波：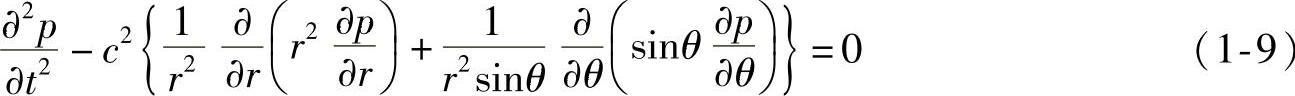

例如，以无限小半径作呼吸球运动的点声源，在其表面即会发生球面波。

此时，可以引入下式所表达的速度势Φ，这样能更容易理解。

点声源时，可以得到如下的结果

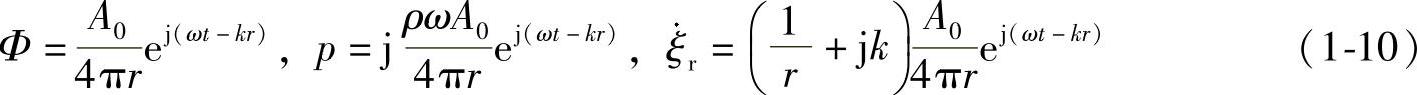(www.xing528.com)

例如，两个强度相同的点声源，其相位差为ϕ，速度势表达为

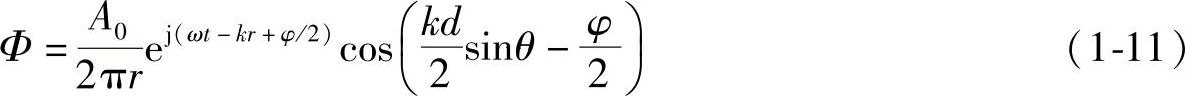
更加具体的例子，考虑微小单元dS以正弦波v₀e^jωt运动的活塞式声源，此时，因球面波的作用，在距离r处所发生的声压有如下解

该式是计算从振动体上所发生的放射声源时的基础式。

其次，关于振动与放射噪声之间的关系，概述如下。

首先，面积为S的平板以2次平均速度<v²>运动时，放射声功率可以用下式表达，其中，σ为放射声功率系数。

W=σρc<v²>S（1-13）

如图1-4所示，来考察无限平板中的自由弯曲波所产生的放射声功率问题。x方向的弯曲波速度为C_B，y方向的弯曲波速度为v（x）

此处，波数k_B=ω/C_B。在弯曲波的作用下，（x，y）空间内所产生的放射声波p（x，y）为

p必须满足波动方向式Δ²p+k²p=0，因此

当y=0时，声波的粒子速度u（x，y）为

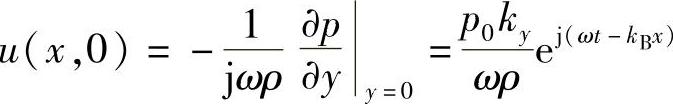
由于与平板的振动速度相等，因此

将式（1-15）、式（1-16）代入式（1-12），放射声压可以表达为

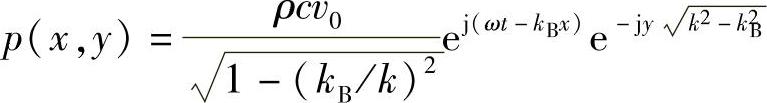
该式所表达的弯曲波传播速度k_B和周围介质中的声速k之间有如下关系：

1）k_B=k（f=f_C）：弯曲波的传播速度和周围介质中的声速相等时，放射波沿与平板平行的方向传播，在某一点、某一时刻与上一个声波重合，声波被无限放大。

此时的频率f_C为临界频率

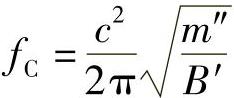
式中，m″为平板单位面积上的质量；B′为单位宽度上的弯曲刚度。

2）k_B<k（f>f_C）：弯曲波的传播速度大于周围介质中的声速时，平板上的声压和振动速度相位相同。

此时平板的单位面积上所放射的声功率为

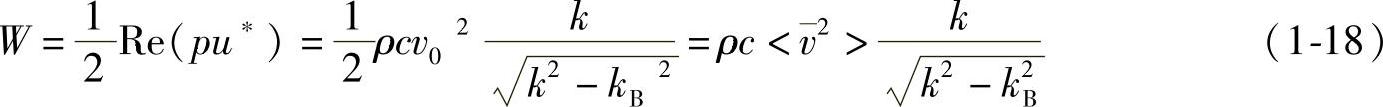
据此，声功率放射率可以表达为

3）k_B>k（f<f_C）：弯曲波的传播速度小于周围介质中的声速时，放射声压可以表达为

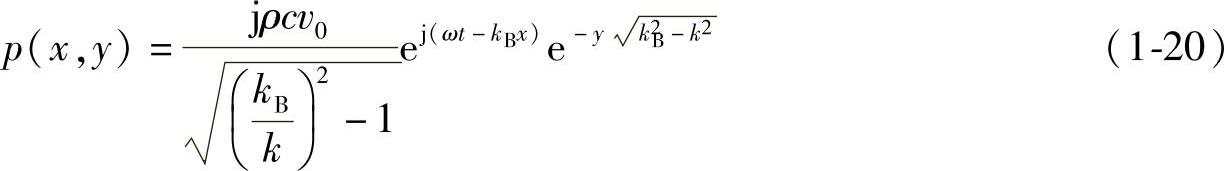
此时，平板上的声压与振动速度有90°的相位差，无法向平板周围介质中放射声波，随着介质中的声压从平板离散而急剧减少。上述结果，形成在无限平板中传播的自由弯曲波的声放射特性，如图1-4所示。

关于有限面积平板振动产生的放射声压，必须要检查其振动模态。例如，周边单纯支持的大小为a×b的平板，以（m，n）模式振动时的放射声功率可以按照式（1-21）推导，其计算结果如图1-5所示。

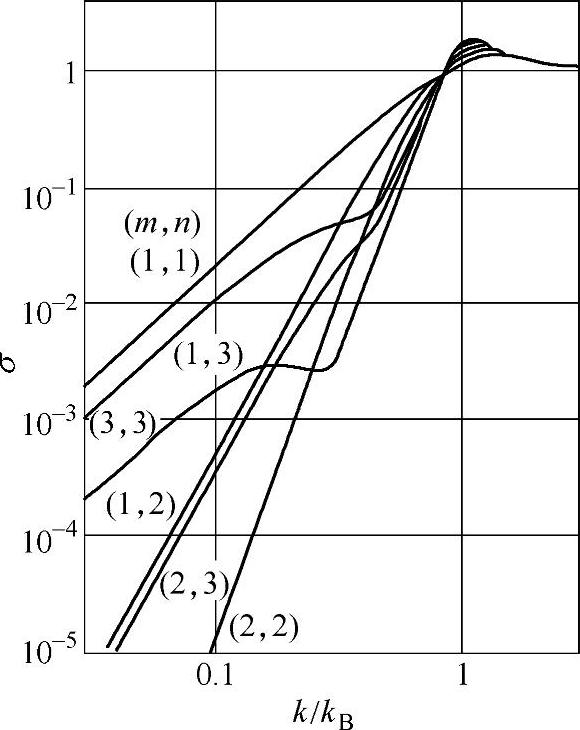
图1-4 无限平板中传播的自由弯曲波特性

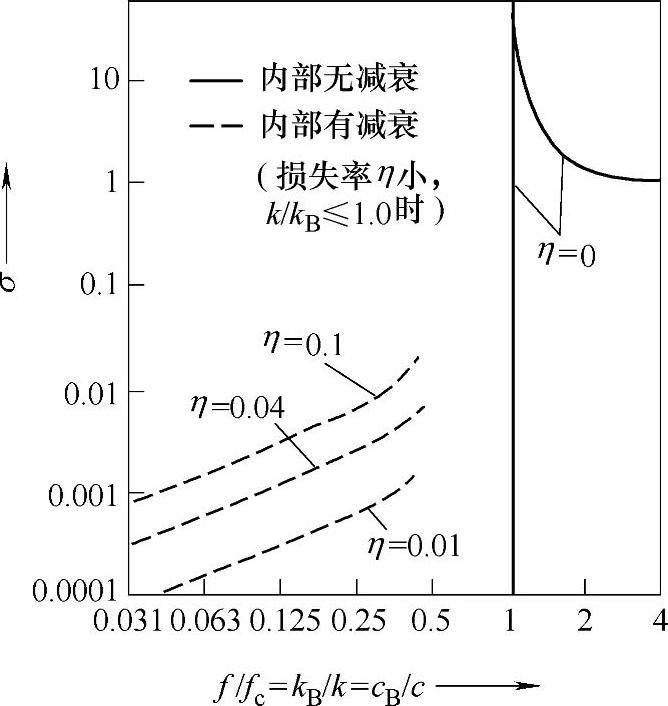
图1-5 正方形平板声音放射功率