1.大型土石方工程量计算
(1)横截面法计算土方量。横截面法适用于地形起伏变化较大或形状狭长地带,其方法是:首先,根据地形图及总平面图,将要计算的场地划分成若干个横截面,相邻两个横截面距离视地形变化而定。在起伏变化大的地段,布置密一些(即距离短一些),反之则可适当疏一些。然后,实测每个横截面特征点的标高,量出各点之间距离(若测区已有比较精确的大比例尺地形图,也可在图上设置横截面,用比例尺直接量取距离,按等高线求算高程,方法简捷,但就其精度来说,没有实测的高),按比例尺把每个横截面绘制到厘米方格纸上,并套上相应的设计断面,则自然地面和设计地面两轮廓线之间的部分,即需要计算的施工部分。
其具体计算步骤如下:
1)划分横截面。根据地形图(或直接测量)及竖向布置图,将要计算的场地划分横截面A—A′,B—B′,C—C′,……划分原则为垂直等高线或垂直主要建筑物边长,横截面之间的距离可不等,地形变化复杂的间距宜小,反之宜大一些,但是最大不宜大于100m。
2)画截面图形。按比例画每个横截面的自然地面和设计地面的轮廓线。自然地面和设计地面轮廓线之间的部分,即为填方和挖方的截面图形。
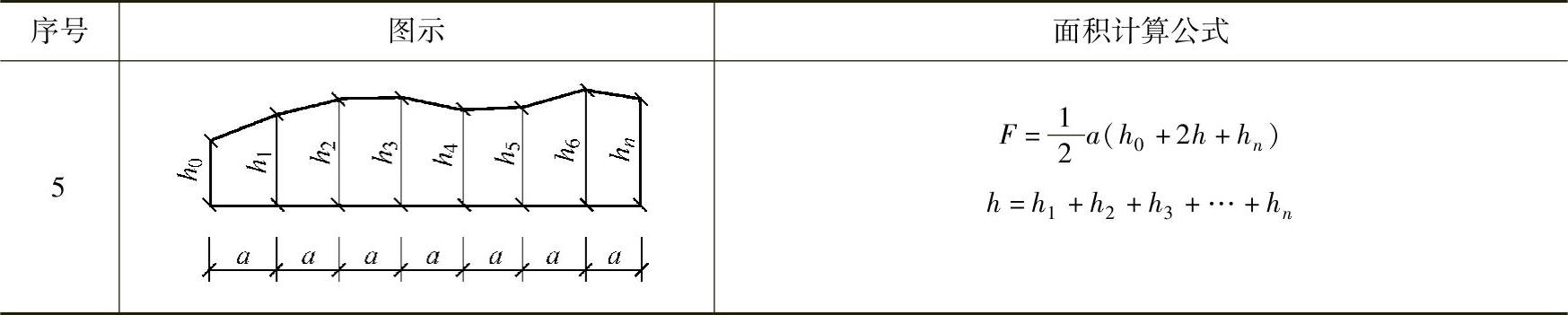
3)计算横截面面积。按表3-21的面积计算公式,计算每个截面的填方或挖方截面积。
表3-21 常用横截面计算公式
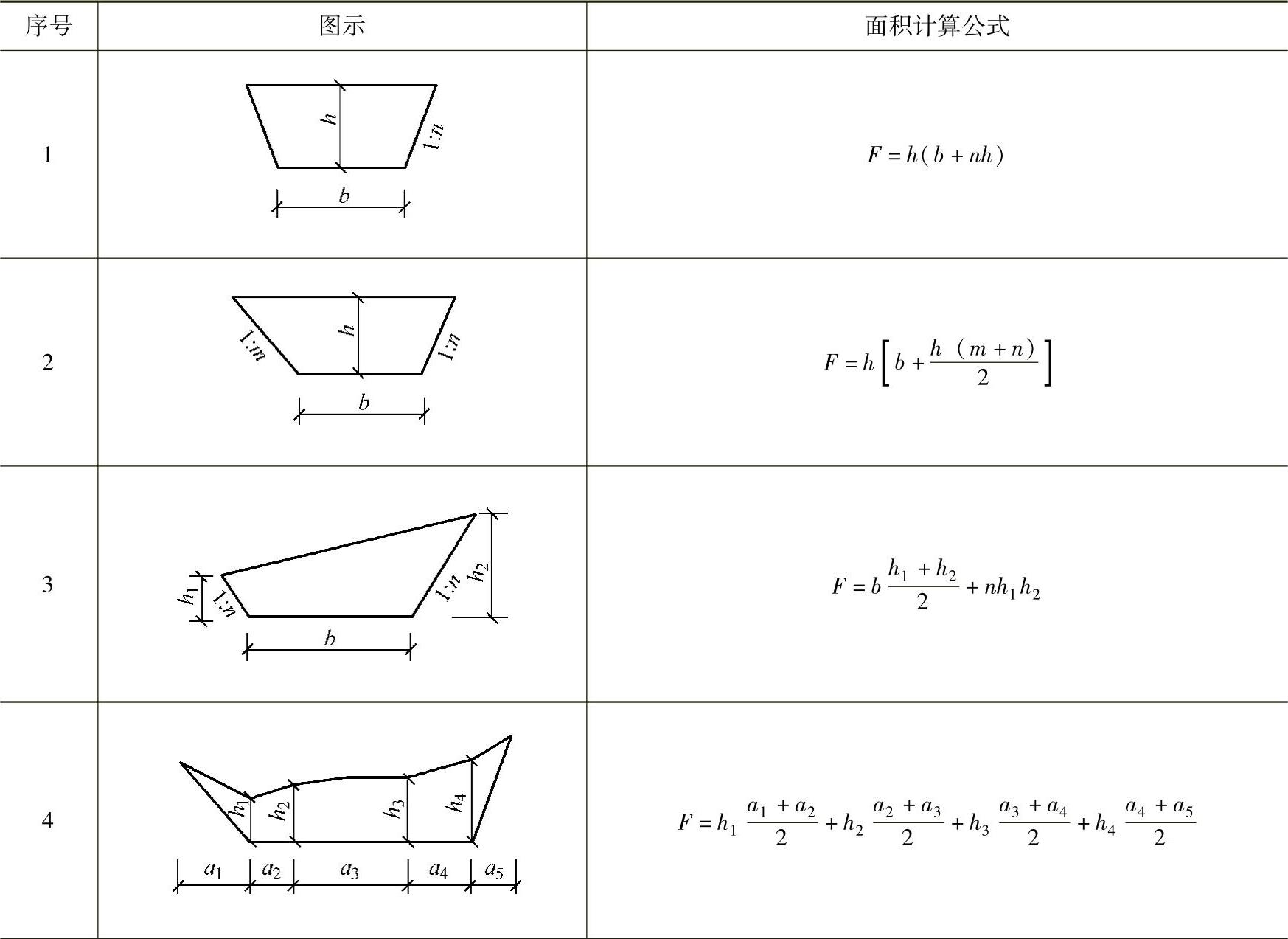
(续)
4)计算土方量。根据截面面积计算土方量,即

式中 V——相邻两截面间的土方量,m3;
F1,F2——相邻两截面的挖(填)方截面积,m2;
L——相邻两截面间的距离,m。
5)按土方量汇总。
(2)方格网法计算土方量。方格网法是把平整场地的设计工作和土方量计算工作结合在一起进行的。
1)划分方格网。在附有等高线的地形图(图样常用比例为1∶500)上作方格网,方格各边最好与测量的纵、横坐标系统对应,并对方格及各角点进行编号。方格尺寸在园林工程中一般用20m×20m或40m×40m。然后将各点设计标高和原地形标高分别标注于方格桩点的右上角和右下角,再将原地形标高与设计地面标高的差值(即各角点的施工标高)填在方格点的左上角,挖方为(+)、填方为(-)。
其中原地形标高用插入法求得(图3-17),方法是:设Hx为欲求角点的原地面高程,过此点作相邻两等高线间最小距离L,则

式中 Ha——低边等高线的高程;
x——角点至低边等高线的距离;
h——等高差。
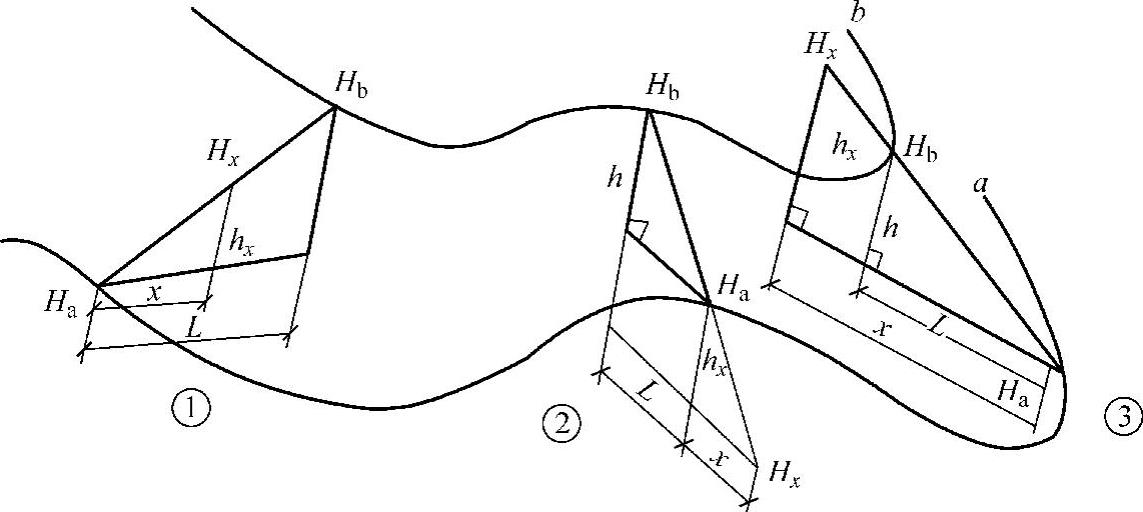
图3-17 插入法求任意点高程示意图
插入法求某点地面高程通常会遇到以下3种情况:
①待求点标高Hx在两等高线之间,如图3-17中①所示,则

②待求点标高Hx在低边等高线的下方,如图3-17中②所示,则

③待求点标高Hx在低边等高线的上方,如图3-17中③所示,则

在平面图上线段HaHb是过待求点所做的相邻两等高线间最小水平距离L。求出的标高数值一一标记在图上。
2)求施工标高。施工标高指方格网各角点挖方或填方的施工高度,其导出式为
施工标高=原地形标高-设计标高(3-6)
从式(3-6)看出,要求出施工标高,必须先确定角点的设计标高。为此,具体计算时,要通过平整标高反推出设计标高。设计中通常取原地面高程的平均值(算术平均或加权平均)作为平整标高。平整标高的含义就是将一块高低不平的地面在保证土方平衡的条件下,挖高垫低使地面水平,这个水平地面的高程就是平整标高。它是根据平整前和平整后土方数相等的原理求出的。当平整标高求得后,就可用图解法或数学分析法来确定平整标高的位置,再通过地形设计坡度,可算出各角点的设计标高,最后将施工标高求出。
3)零点位置。零点是指不挖不填的点,零点的连线即为零点线,它是填方与挖方的界定线,因而零点线是进行土方计算和土方施工的重要依据之一。要识别是否有零点存在,只要看一个方格内是否同时有填方与挖方,如果同时有,则说明一定存在零点线。为此,应将此方格的零点求出,并标于方格网上,再将零点相连,即可分出填挖方区域,该连线即为零点线。
零点可通过下式求得,如图3-18a所示,有

式中 x——零点距h1一端的水平距离,m;
h1,h2——方格相邻二角点的施工标高绝对值,m;
a——方格边长。
零点的求法还可采用图解法,如图3-18b所示。方法是将直尺放在各角点上标出相应的比例,而后用尺相接,与方格相交的点为零点位置。
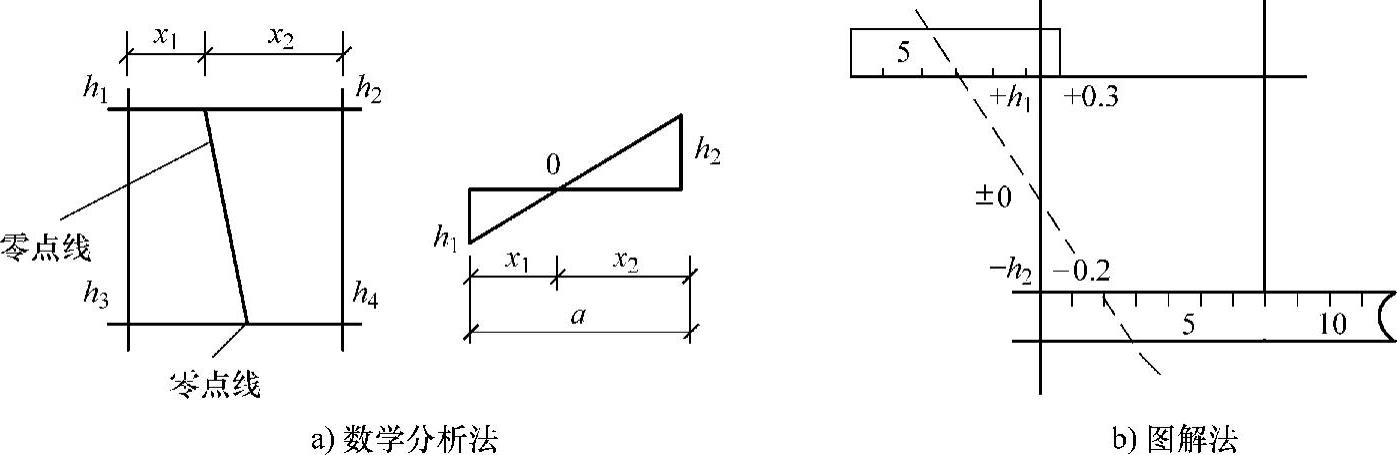
图3-18 求零点位置示意图
4)计算土方工程量。根据各方格网底面积图形以及相应的体积计算公式(表3-22)来逐一求出方格内的挖方量或填方量。
表3-22 方格网计算土方量计算公式表
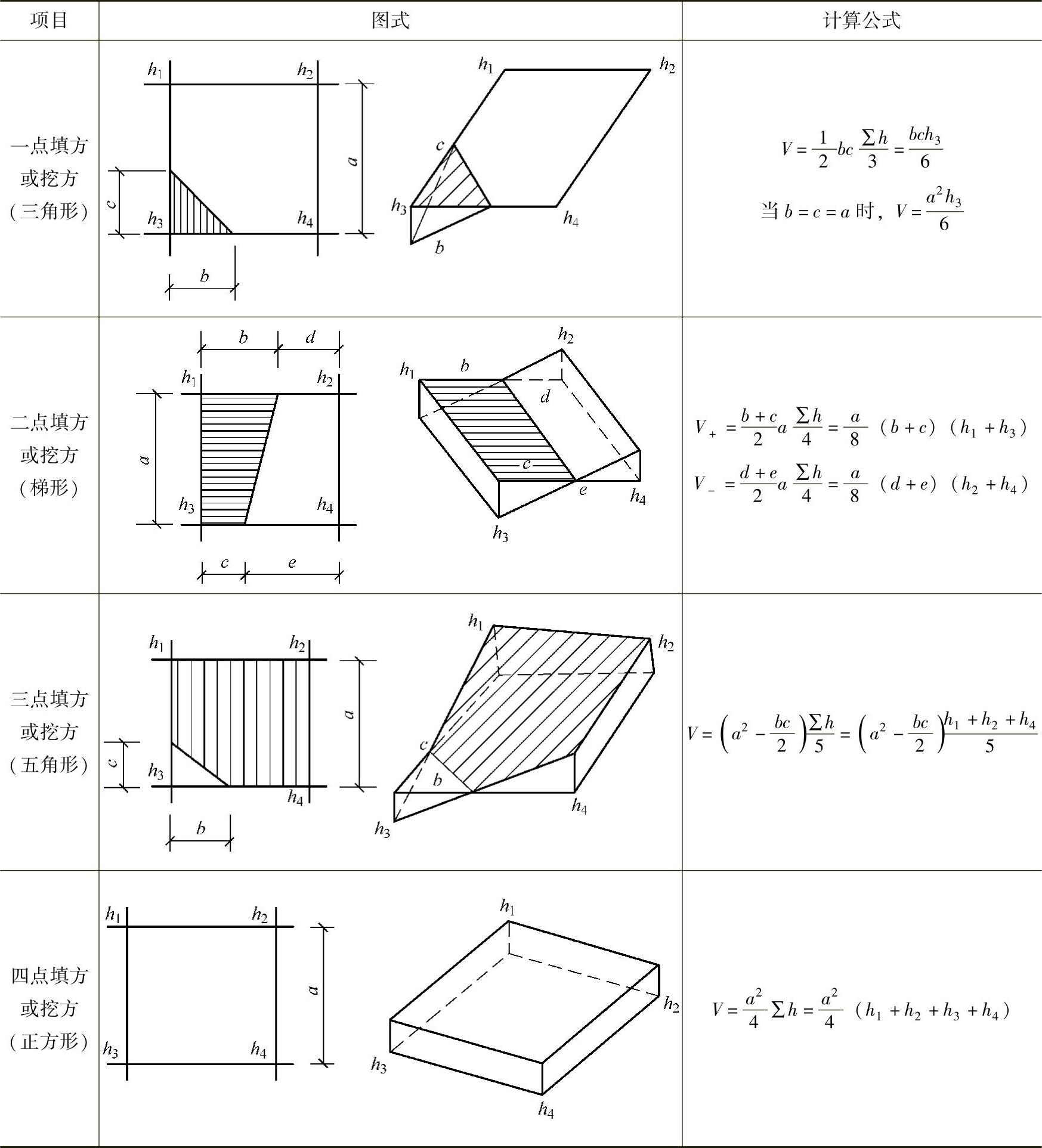
注:1.a为方格网的边长,m;b、c为零点到一角的边长,m;h1,h2,h3,h4为方格网四点脚的施工高程,m;用绝对值代入;∑h为填方或挖方施工高程的总和,m,用绝对值代入;V为挖方或填方体积,m3。
2.本表公式是按各计算图形底面乘以平均施工高程而得出的。
5)计算土方总量。将填方区所有方格的土方量(或挖方区所有方格的土方量)累计汇总,即得到该场地填方和挖方的总土方量,最后填入汇总表。
2.其他挖填方相关数据
1)各种土的最优含水量和最大密实度参考数值见表3-23。
表3-23 土的最优含水量和最大密实度参考表

2)压实机械和工具每层铺土厚度与所需的碾压(夯实)遍数的参考数值见表3-24。
表3-24 填方每层铺土厚度和压实遍数
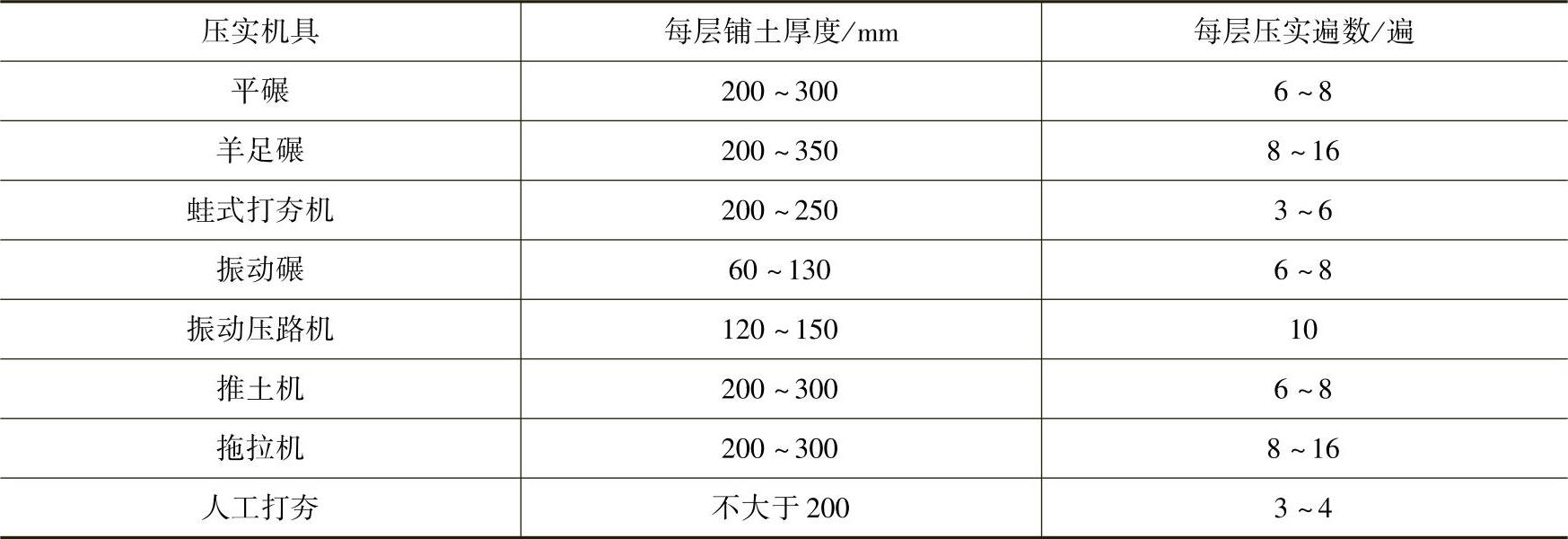
注:人工打夯时土块粒径不应大于5cm。
3)利用运土工具行驶来压实时,每层铺土厚度不得超过表3-25规定的数值。
表3-25 运土工具压实填方参考值 (单位:m)

4)挖方工程的放坡做法见表3-26和表3-27。
表3-26 不同的土质自然放坡坡度允许值
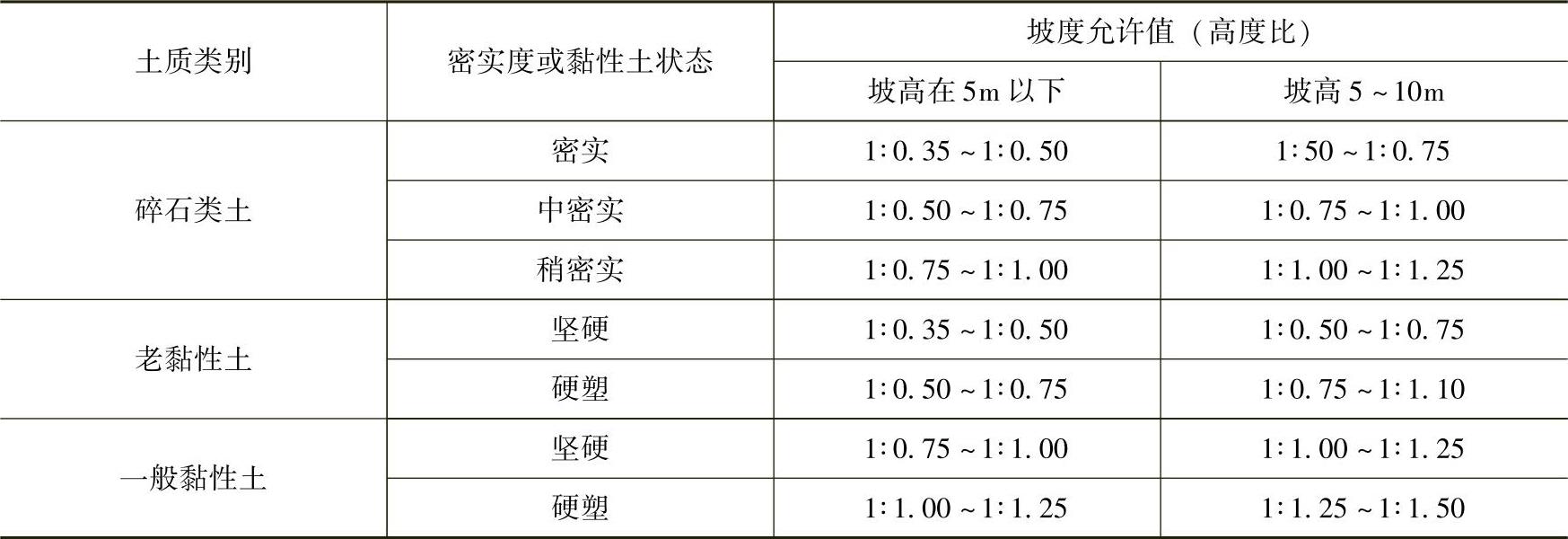
表3-27 一般土壤自然放坡坡度允许值

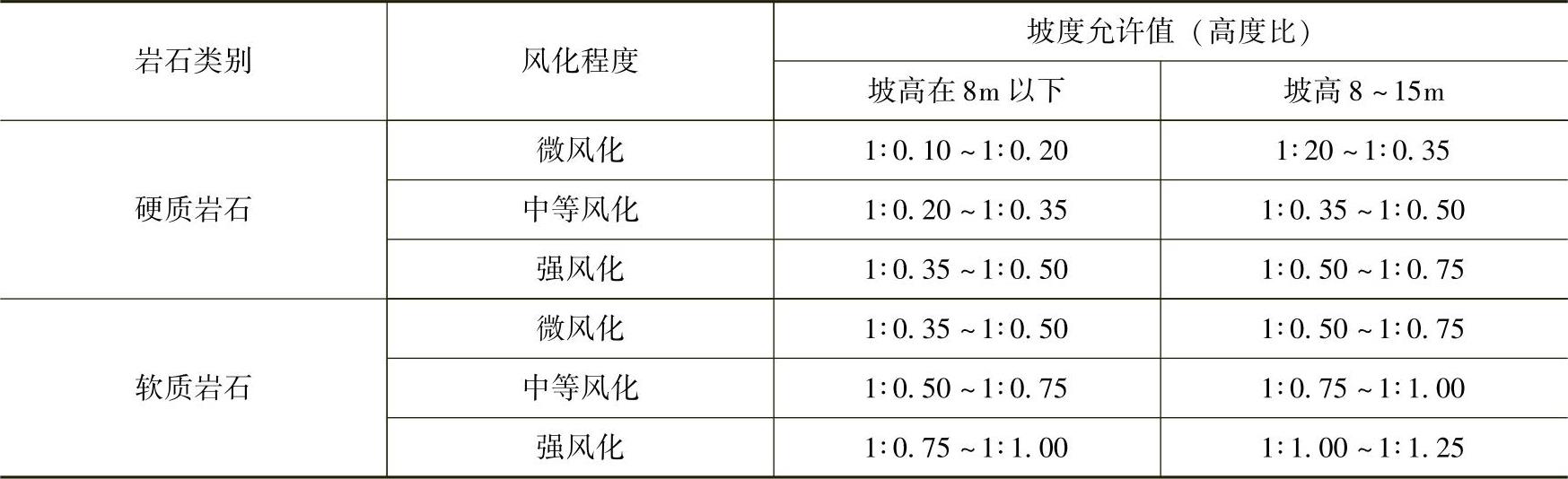
5)岩石边坡的坡度允许值(高宽比)受岩石类别、石质风化程度以及坡面高度三方面因素的影响,见表3-28。
表3-28 岩石边坡坡度允许值
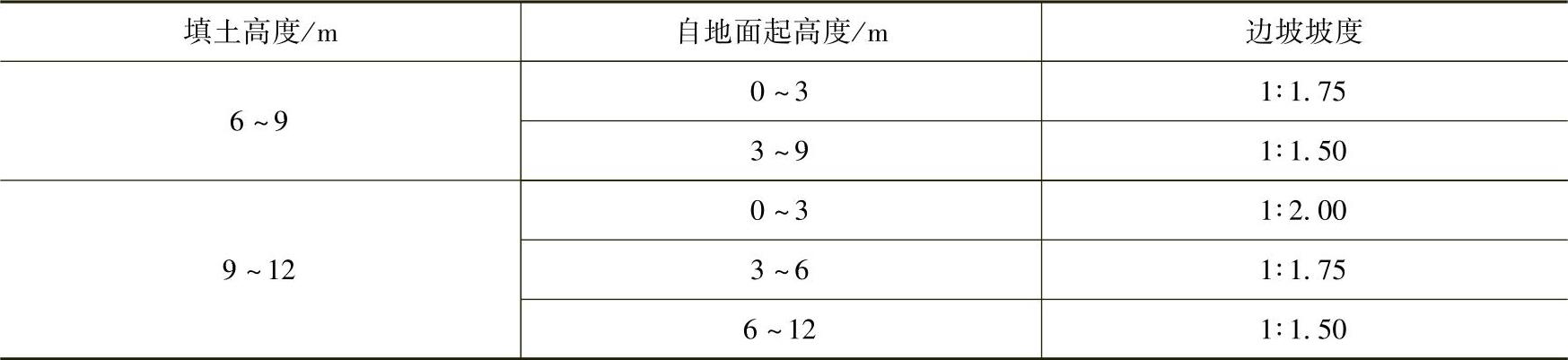
6)填方的边坡坡度应根据填方高度、土的种类及其重要性在设计中加以规定。用黄土或类黄土填筑重要的填方时,其边坡坡度可参考表3-29采用。
表3-29 黄土或类黄土填筑重要填方的边坡坡度
3.各类苗木产品的规格及质量标准
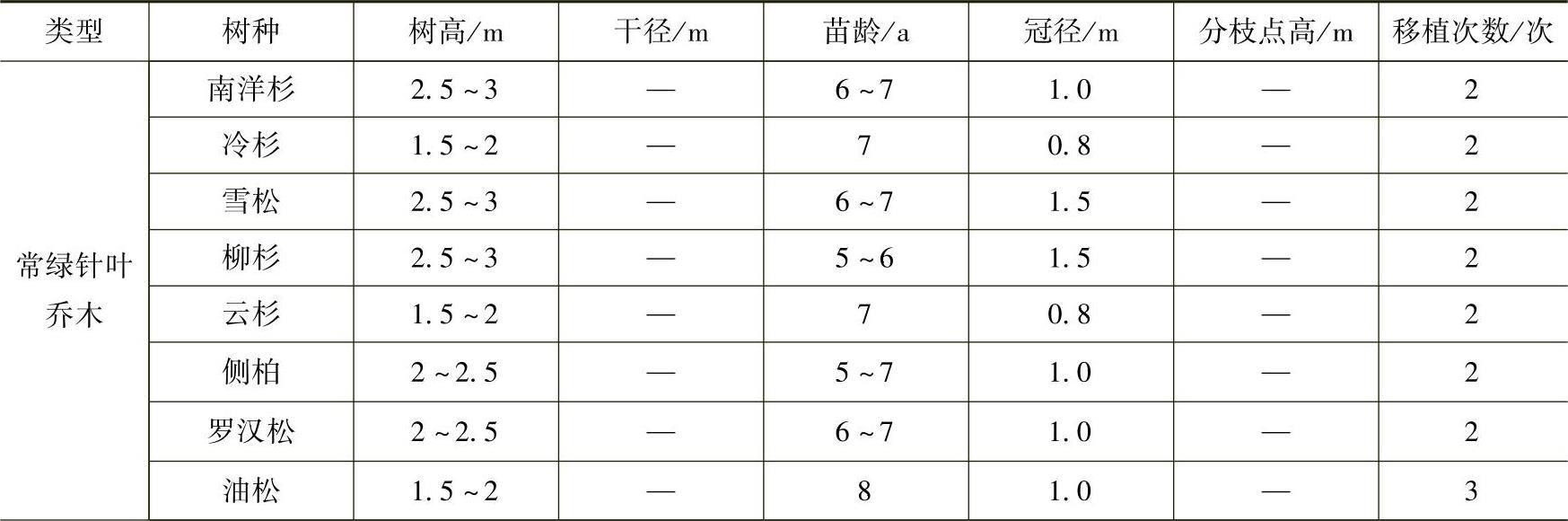
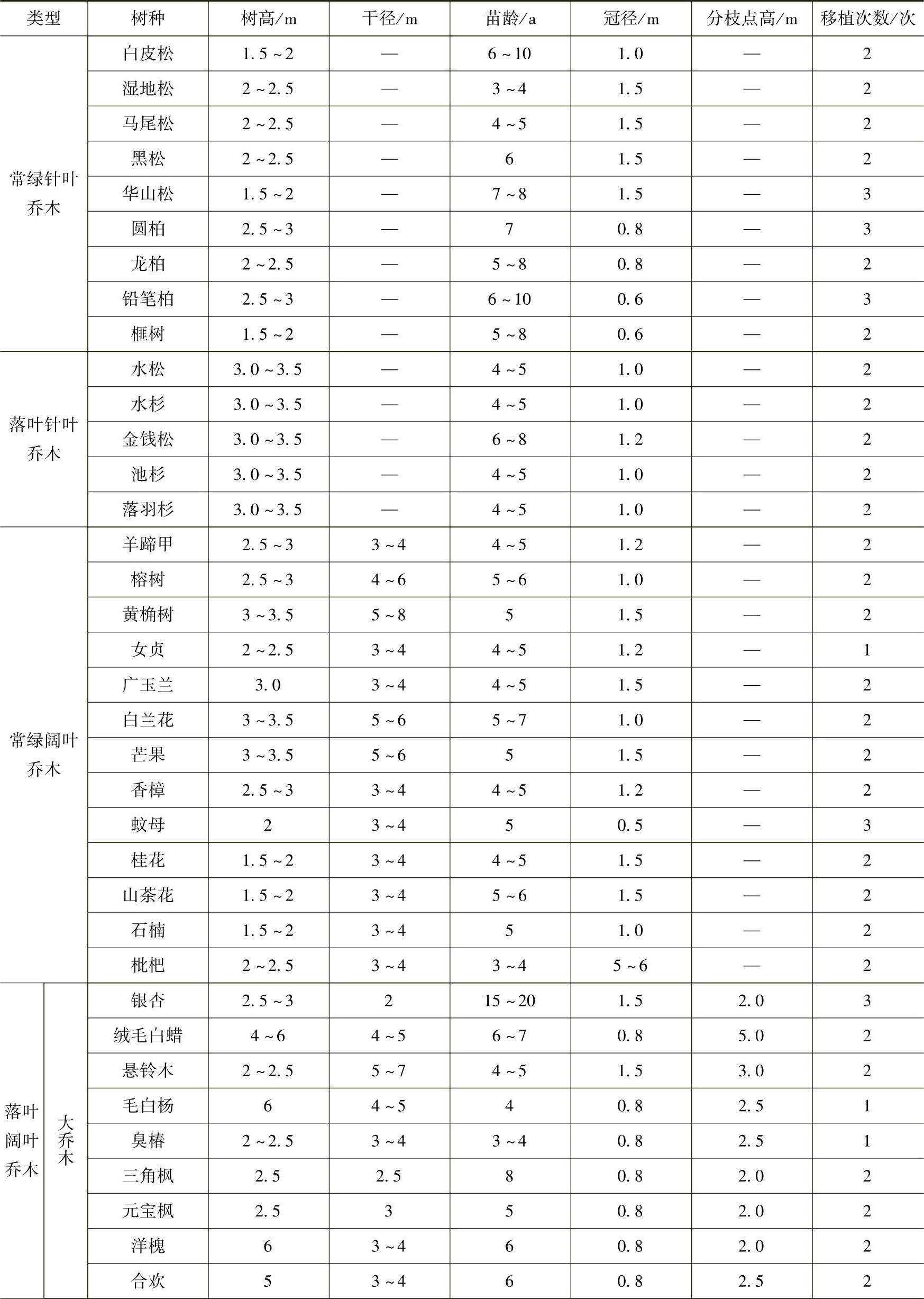
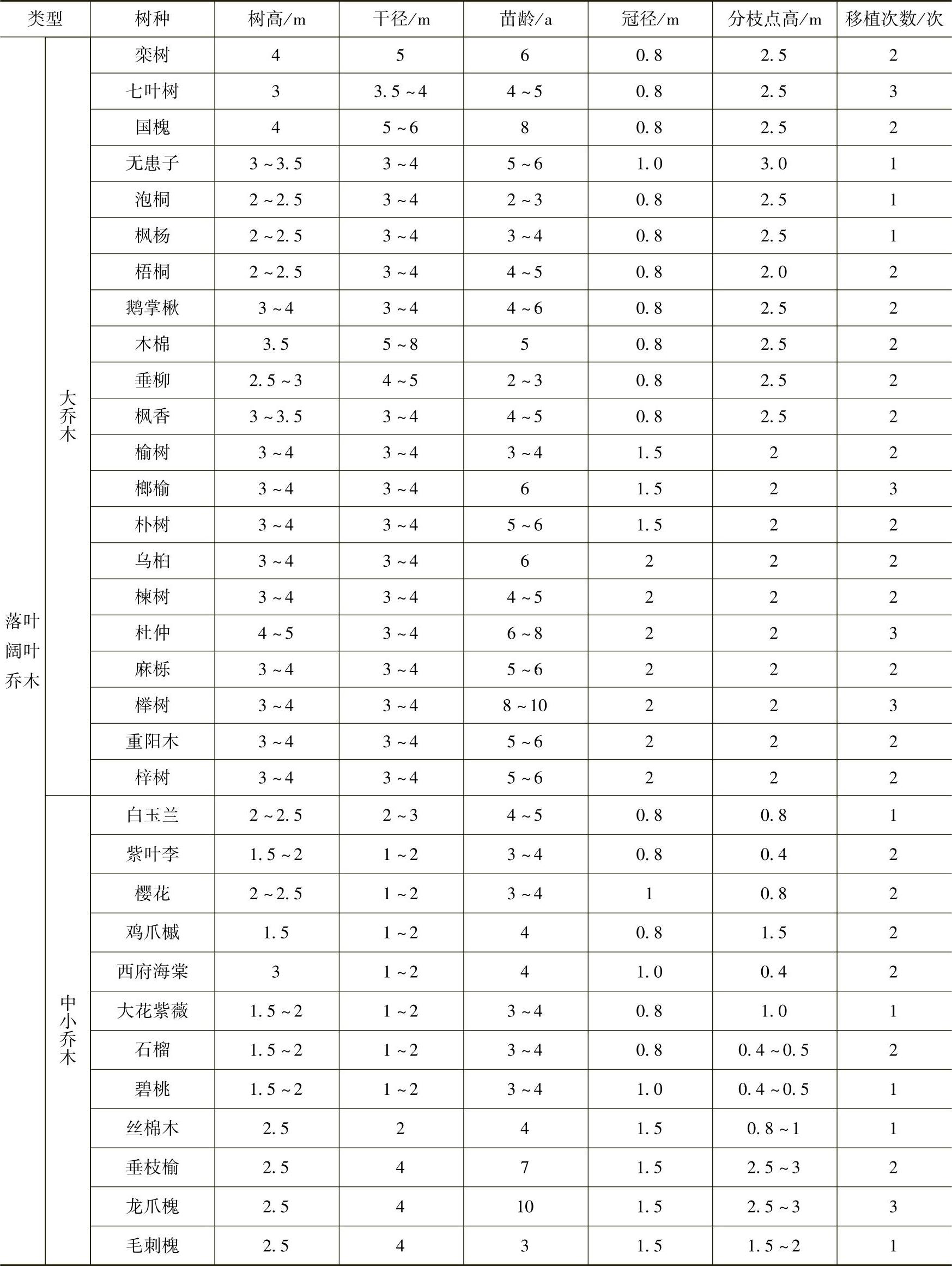
1)乔木类常用苗木产品主要规格质量标准见表3-30。
表3-30 乔木类常用苗木产品的主要规格质量标准
(续)
(续)
2)灌木类常用苗木产品的主要规格质量标准见表3-31。
表3-31 灌木类常用苗木产品的主要规格质量标准
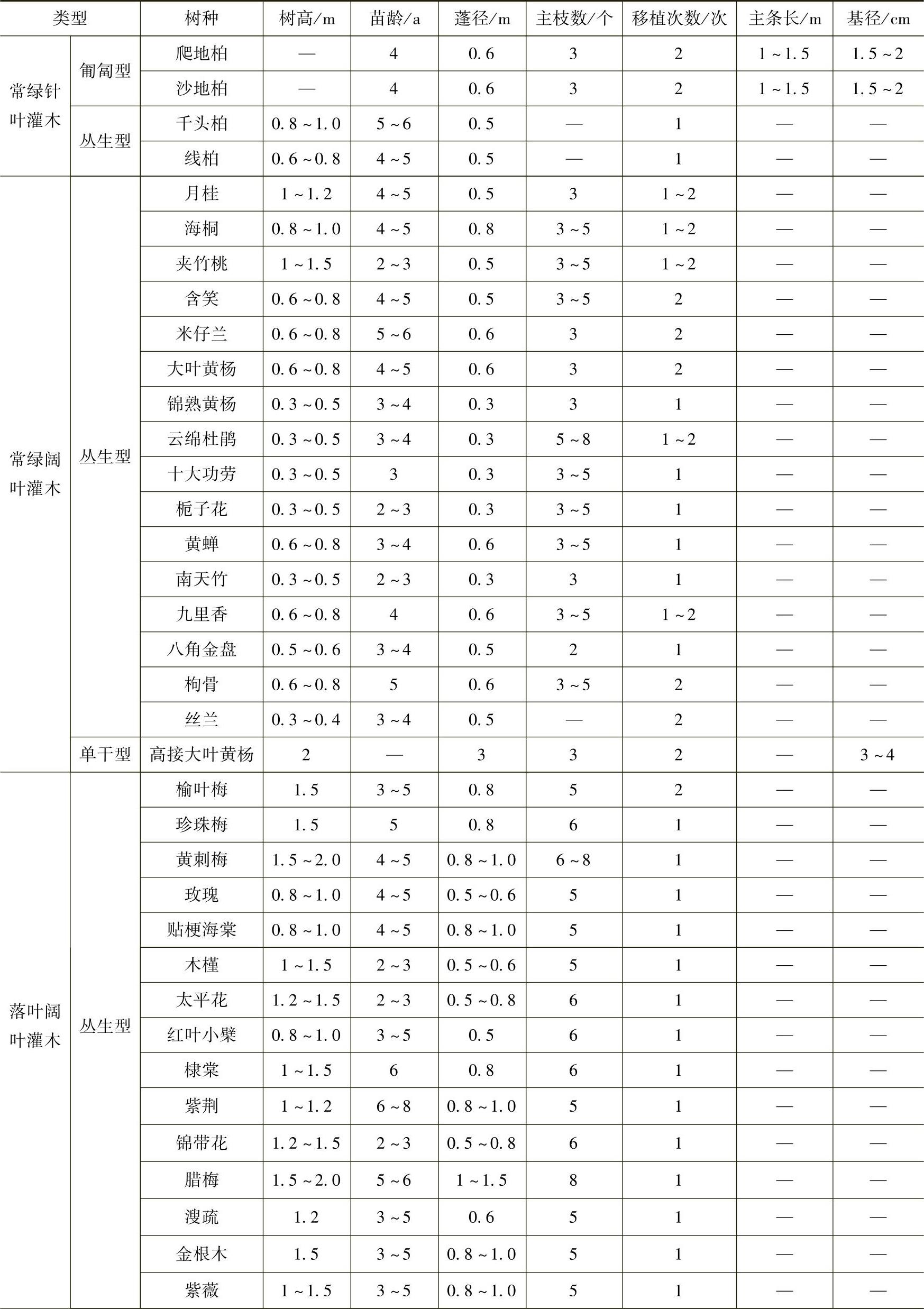
(续)
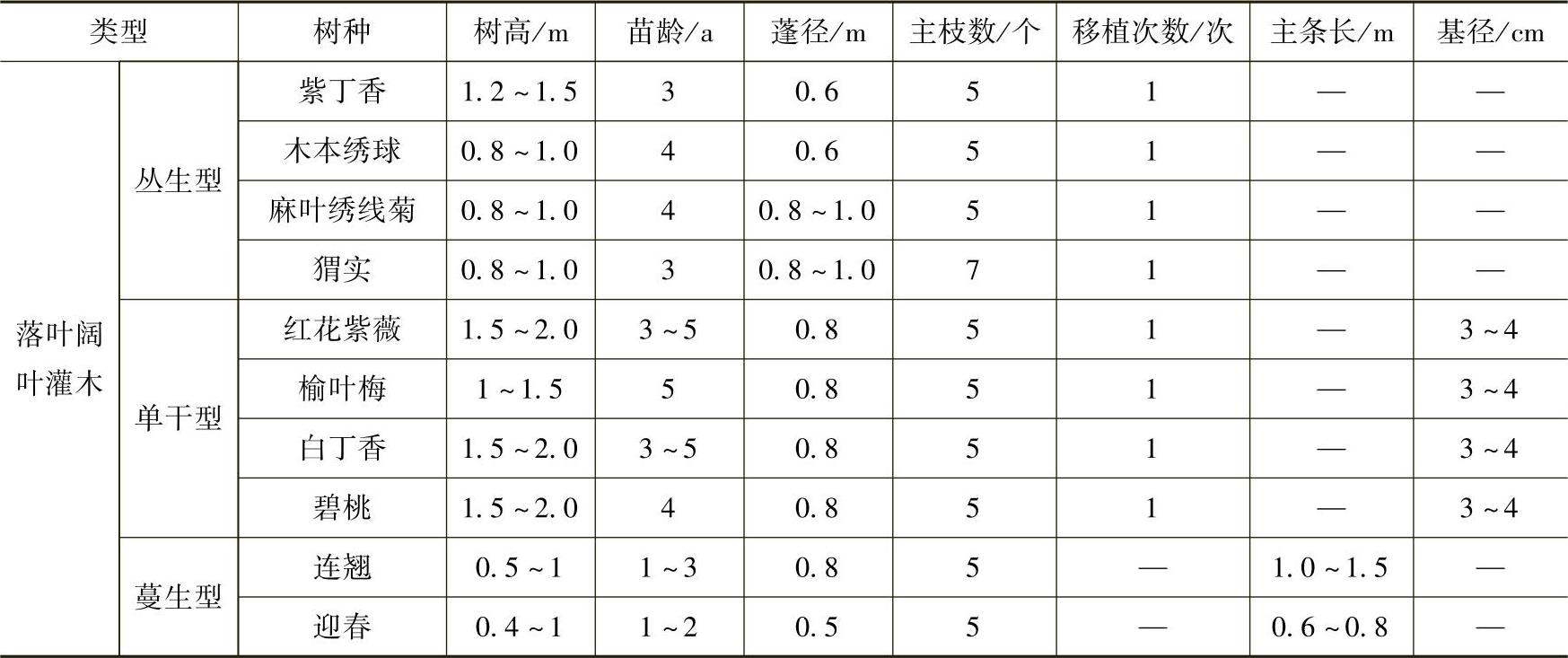
3)藤木类常用苗木产品主要规格质量标准见表3-32。
表3-32 藤木类常用苗木产品主要规格质量标准
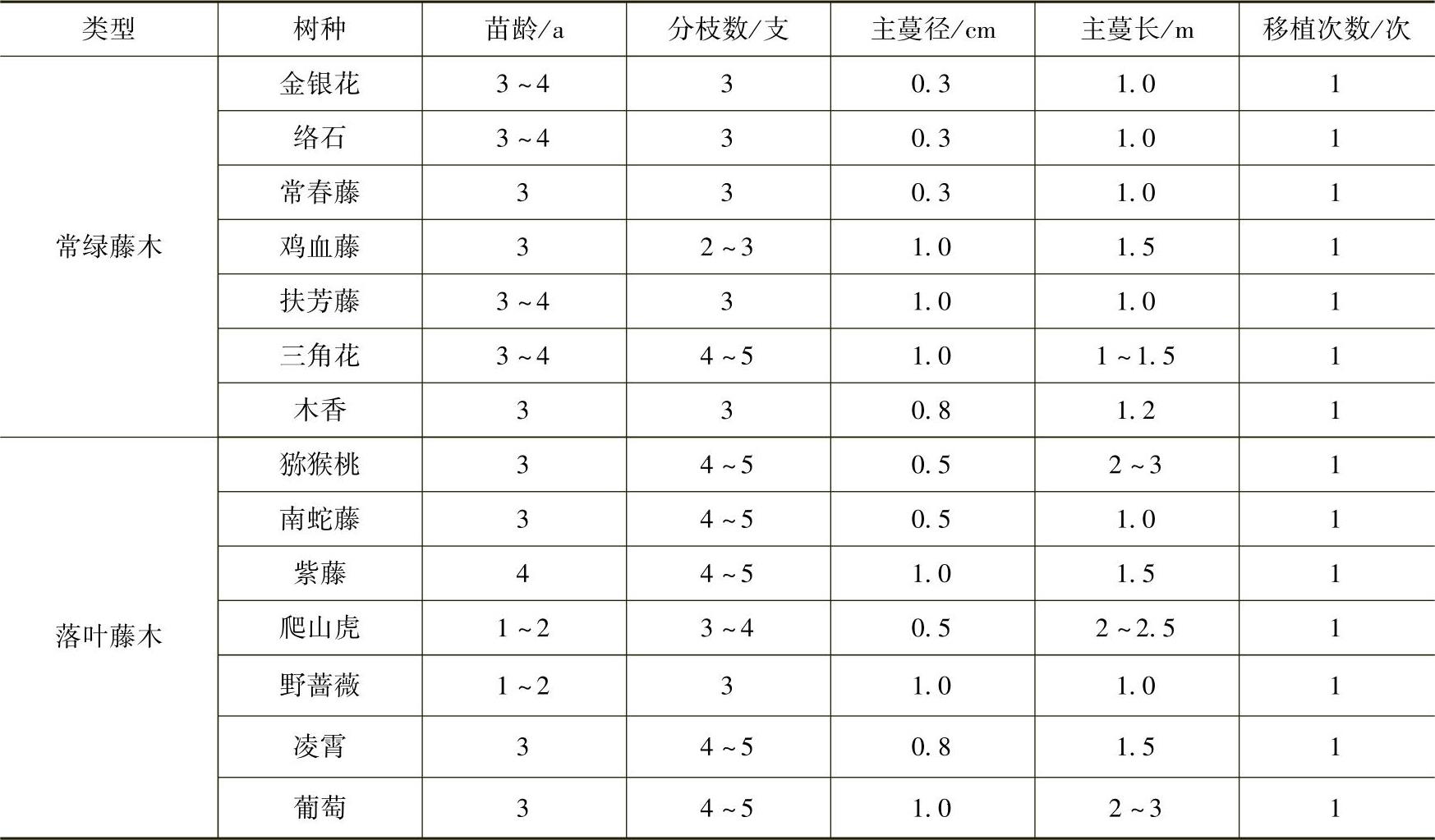
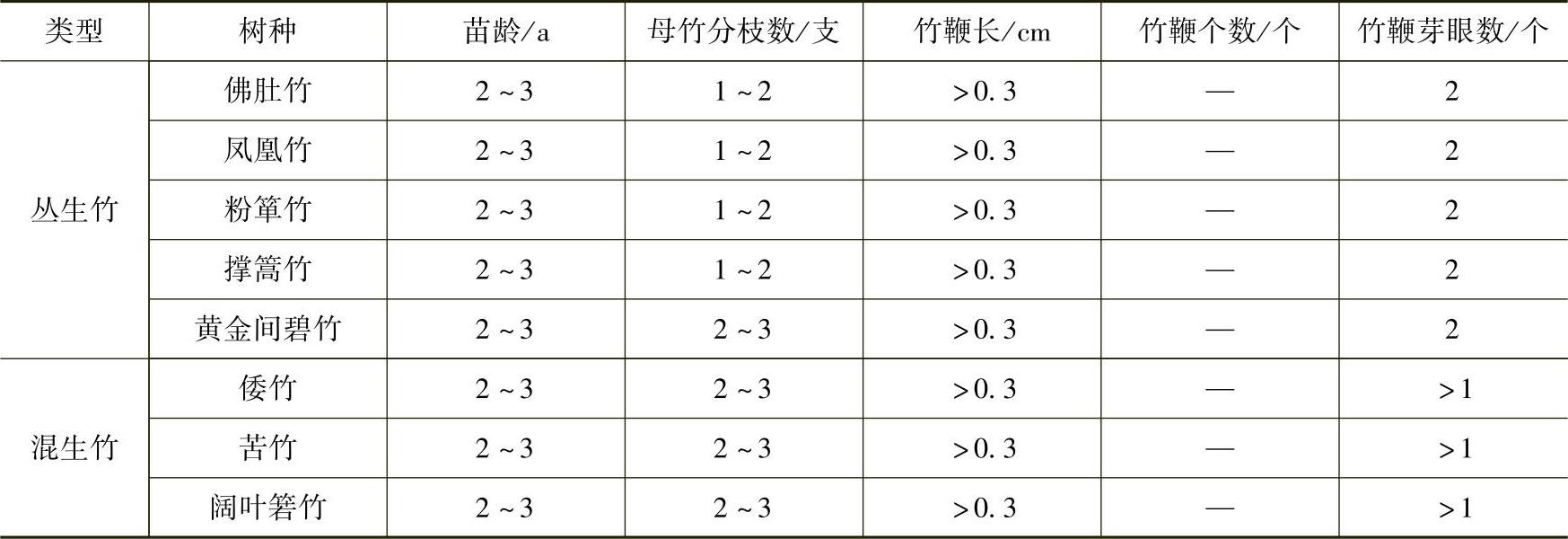
4)竹类常用苗木产品主要规格质量标准见表3-33。
表3-33 竹类常用苗木产品主要规格质量标准
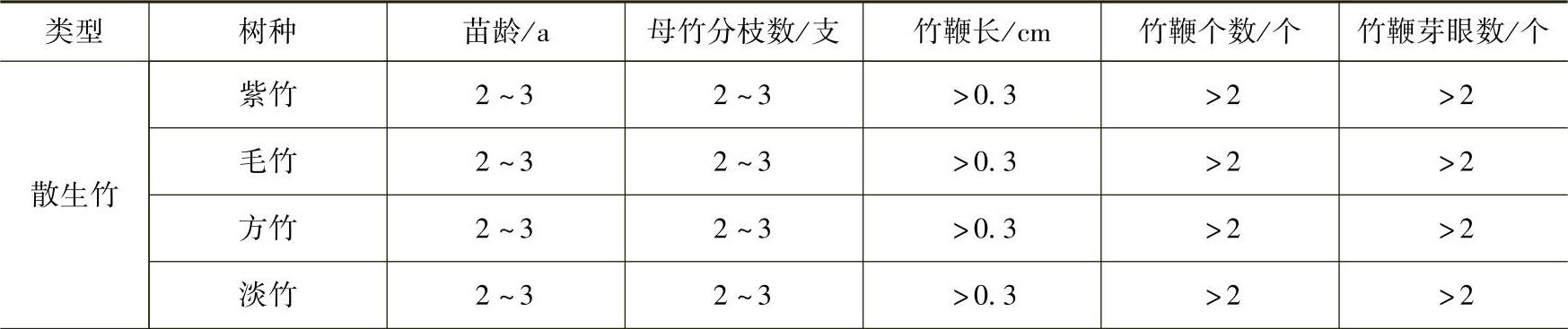
(续)
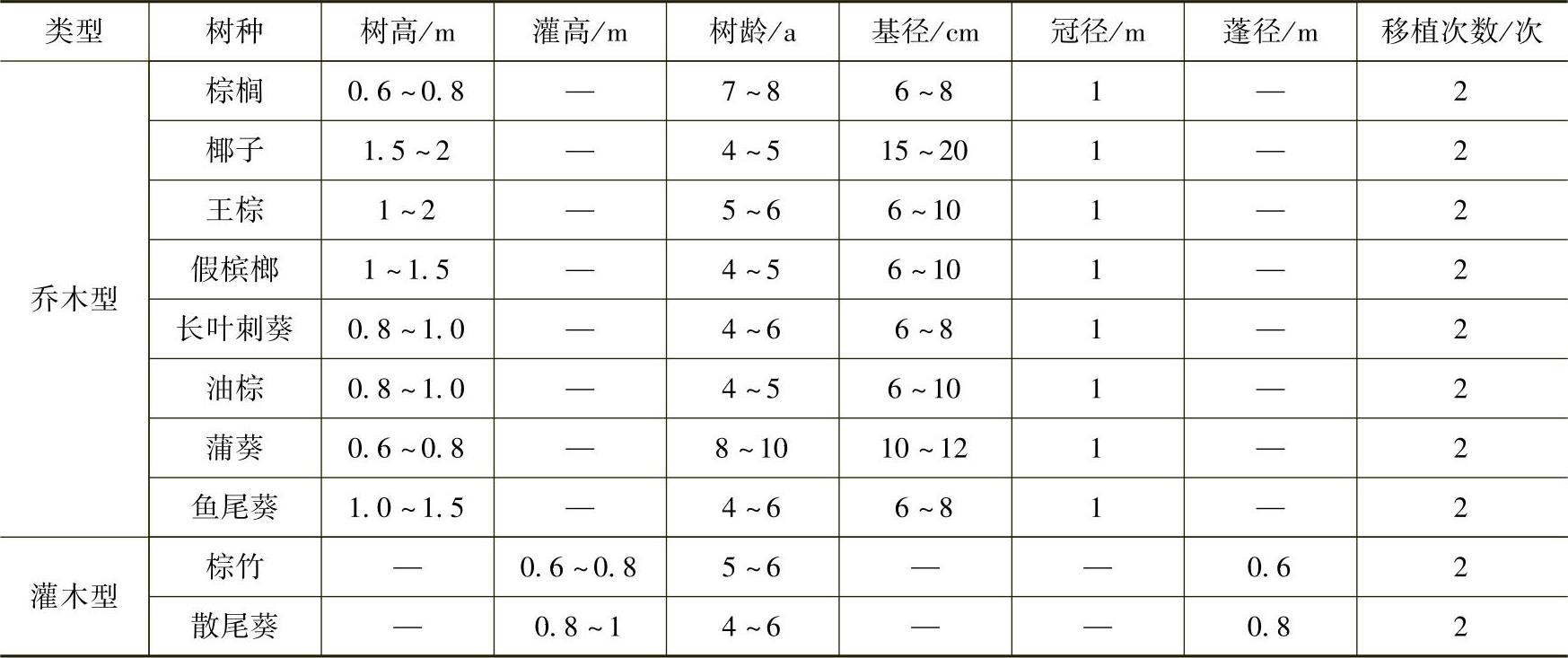
5)棕榈类等特种苗木产品主要规格质量标准见表3-34。
表3-34 棕榈类等特种苗木产品主要规格质量标准
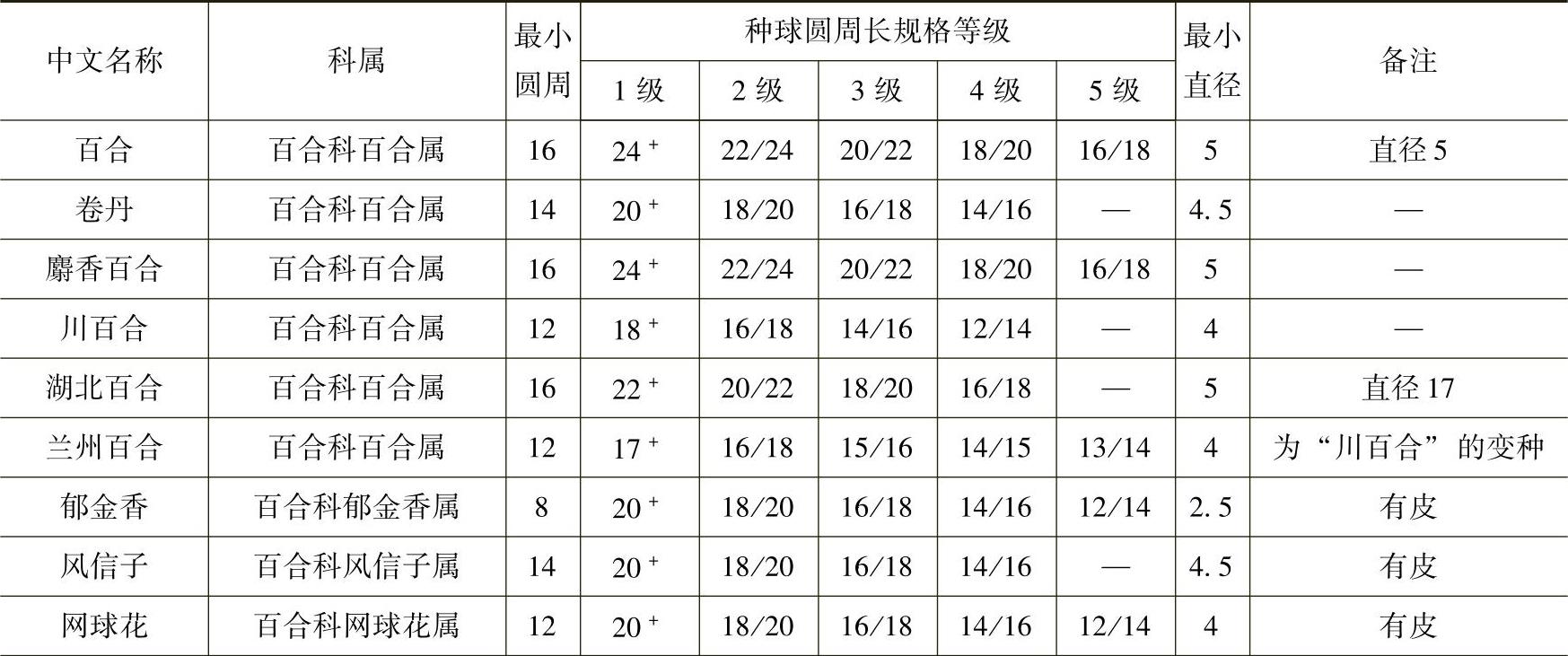
6)球根花卉种球质量标准。(https://www.xing528.com)
①鳞茎类种球产品规格等级标准应符合表3-35的要求。
表3-35 鳞茎类种球产品规格等级标准 (单位:cm)
(续)
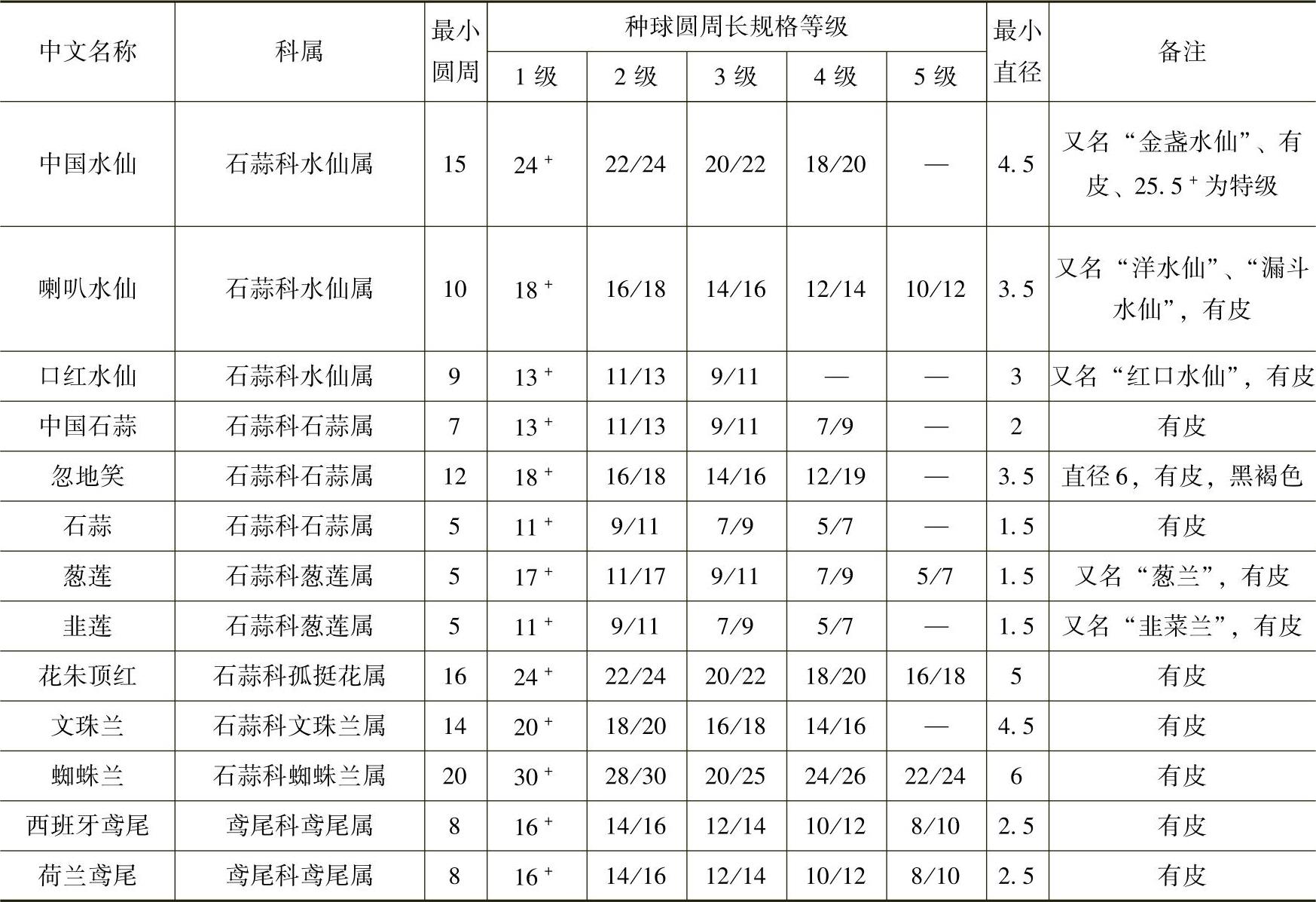
注:“规格等级”栏中24+表示在24cm以上为1级,22/24表示在22~24cm为2级,以下依此类推。
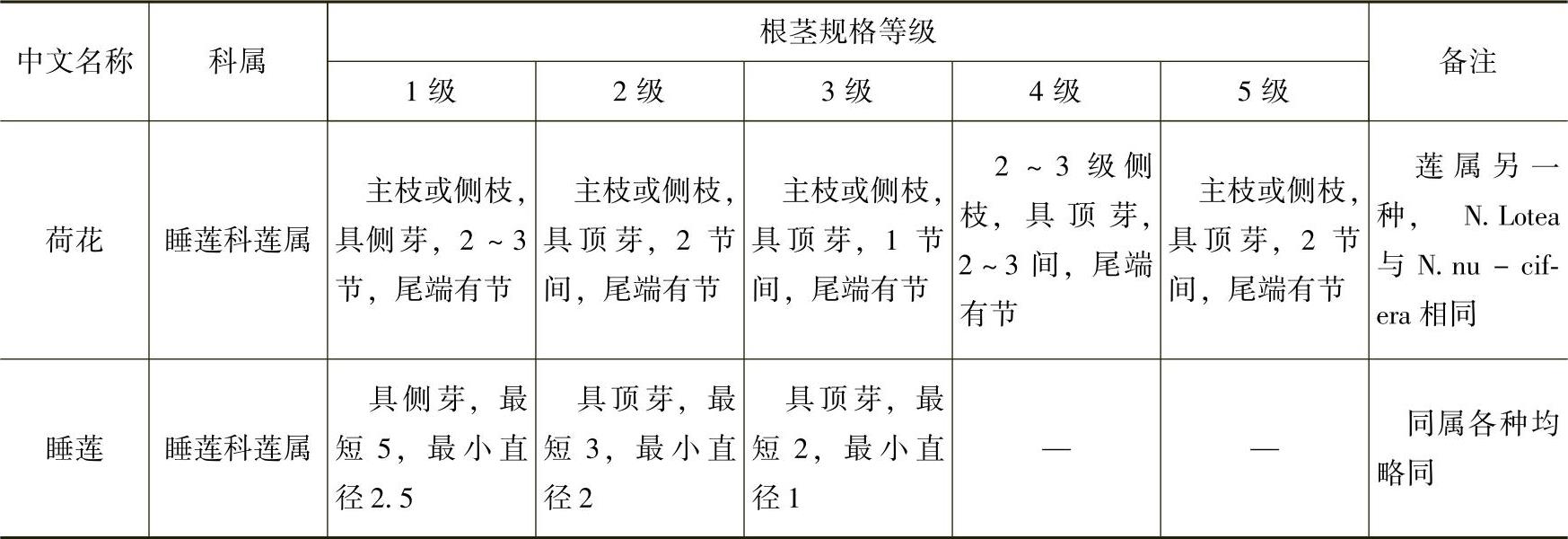
②根茎类种球产品规格等级标准应符合表3-36和表3-37的要求。
表3-36 根茎类种球产品规格等级标准表(一) (单位:cm)

表3-37 根茎类种球产品规格等级标准表(二) (单位:cm)
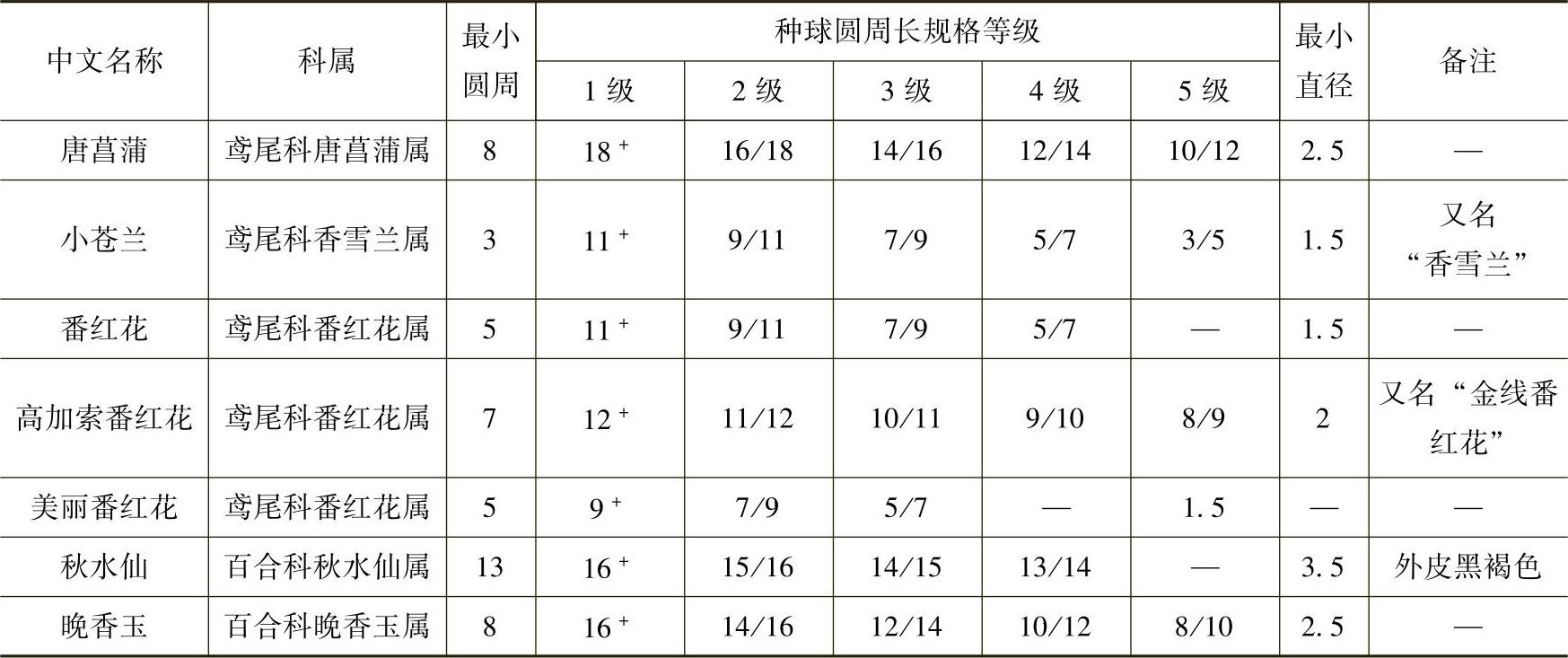
③球茎类种球产品规格等级标准应符合表3-38的要求。
表3-38 球茎类种球产品规格等级标准 (单位:cm)
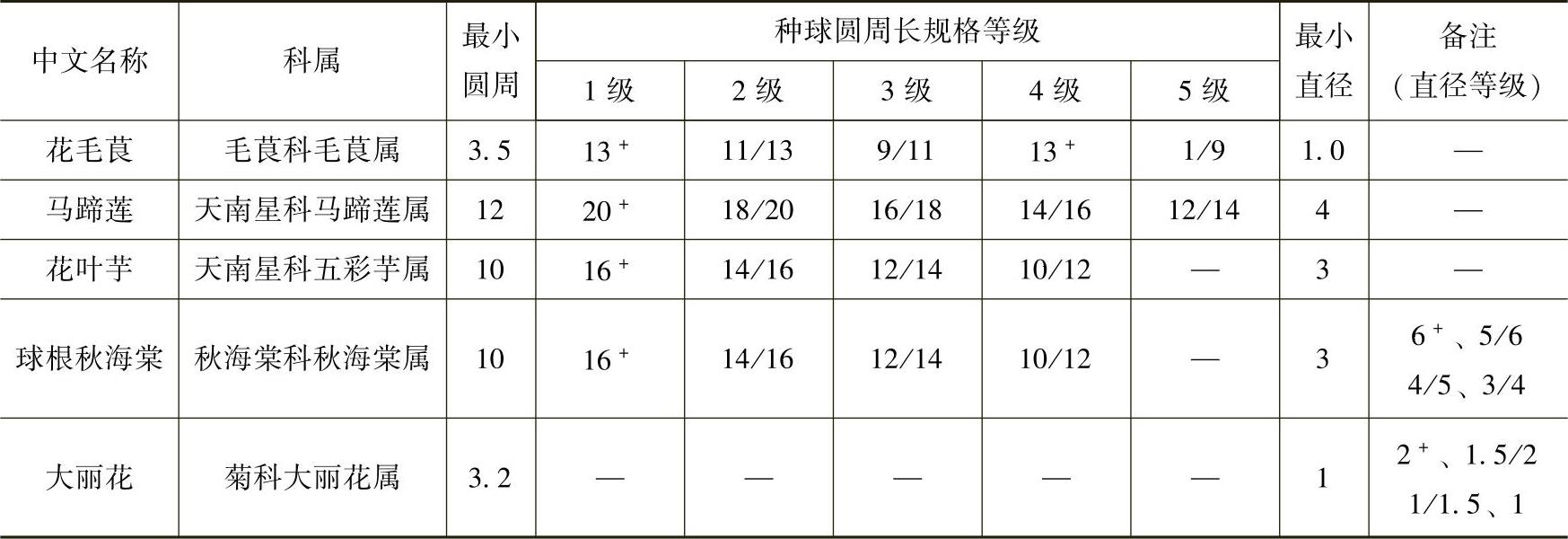
④块茎类、块根类种球产品规格等级标准应符合表3-39的要求。
表3-39 块茎类、块根类产品规格等级标准 (单位:cm)
4.绿地喷灌工程计算常用数据
(1)灌水量计算。喷灌一次的灌水量可采用式(3-8)来计算,即

式中 h——一次灌水量,mm;
h净——根据树种确定的每日每次需要的纯灌水量,mm;
φ——利用系数,一般在65%~85%。
计算时,利用系数φ的确定可根据水分蒸发量大小而定。气候干燥,蒸发量大的喷灌不容易做到均匀一致,而且水分损失多,因此利用系数应选较小值,具体设计时常取φ=70%;如果是在湿润环境中,水分蒸发较少则应取较大的利用系数值。
(2)灌溉时间计算。灌水量多少和灌溉时间的长短有关系。每次灌溉的时间长短可以按照式(3-9)计算确定,即

式中 T——支管或喷头每次喷灌纯工作时间,h;
ρ——喷灌强度,mm/h。
(3)喷灌系统的用水量计算。整个喷灌系统需要的用水量数据,是确定给水管管径及水泵选择所必需的设计依据。这个数据可用式(3-10)求出,即
Q=nq (3-10)
式中 Q——用水量,m3/h;
n——同时喷灌的喷头数;
q——喷头流量,m3/h,q=LbP/1000;
L——相邻喷头的间距,m;
b——支管的间距,m;
P——设计喷灌强度,mm/h。
在采用水泵供水时,显然,用水量Q实际上就是水泵的流量。
(4)水头计算。水头要求是设计喷灌系统不可缺少的依据之一。喷灌系统中管径的确定、引水时对水压的要求及对水泵的选择等,都离不开水头数据。以城市给水系统为水源的喷灌系统,其设计水头可用式(3-11)来计算,即
H=H管+H弯+H喷+H立管高度+H地形高差 (3-11)
式中 H——设计水头,m;
H管——管道沿程水头损失,m;
H弯——管道中各弯道、阀门的水头损失,m;
H喷——最后一个喷头的工作水头,m。
如果公园内是自设水泵的独立给水系统,则水泵扬程(水头)可按式(3-12)算出,即
H=H实+H管+H弯+H喷 (3-12)
式中 H——水泵的扬程,m;
H实——实际扬程等于水泵的扬程与水泵轴到最末一个喷头的垂直高度之和。
喷灌系统设计流量应大于全部同时工作的喷头流量之和。Q=nρ(Q为喷灌系统设计流量,ρ为一个喷头的流盘,mm3/h,n为喷头数量)。水泵功率大小计算可采用式(3-13),即

式中 N——动力功率,hp;
K——动力备用系数,1.1~1.3;
η泵——水泵的效率;
η传动——传动效率,0.8~0.95;
Q泵——水泵的流量,m3/h;
H泵——水泵扬程,m;
γ——水的容重,t/m3。
因为1hp=0.736kW,所以式(3-13)可改为

于是两点之间的水头损失Hf,如图3-19所示。
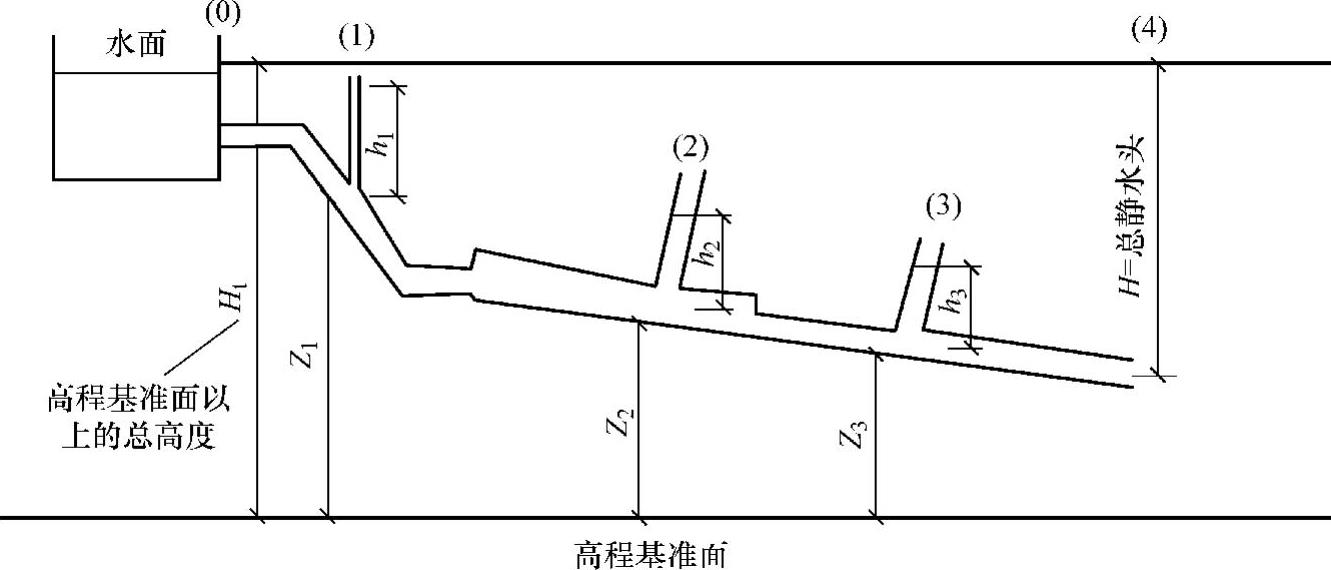
图3-19 有压管流“能量守恒”原理
伯努力定理的数学表达式为
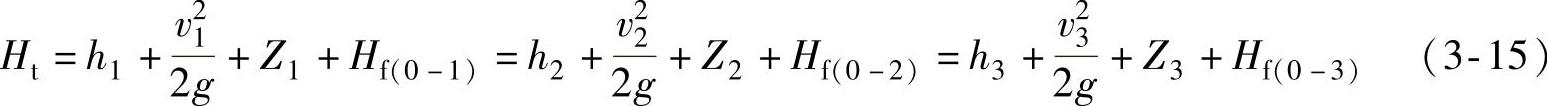
式中 Ht——断面(0)处的总水头,或高程基准面以上的总高度,m;
h1,h2,h3——断面(1)、(2)、(3)处的静水头,即测压管水柱高度,m;
υ1,υ2,υ3——断面(1)、(2)、(3)处管道中的平均流速,m/s;
Z1,Z2,Z3——断面(1)、(2)、(3)处管道轴线高,m;
Hf(0-1),Hf(0-2),Hf(0-3)——断面(0)~(1)、(0)~(2)、(0)~(3)之间的水头损失,
它包括沿程水头损失和局部水头损失,m。
沿程水头损失的计算公式如下:
1)有压管流程水头损失的计算通常采用达西-维斯巴赫公式,即

式中 hf——管道沿程水头损失,m;
λ——管道沿程阻力系数;
l——管道长度,m;
d——管道内径,m;
υ——管道断面平均流速,m/s;
g——重力加速度,为9.81m/s2。
2)管道沿程阻力系数又随管道中水的流态不同而异。对于层流(Re<2300),沿程阻力系数可由式(3-17)求得,即

式中 λ——管道沿程阻力系数;
Re——雷诺数。
对于紊流(Re>2300),沿程阻力系数由试验研究确定。
3)为了便于实际应用,通常将沿程水头损失表示为流量(或流速)的指数函数和管径的指数函数的单项式,即

式中 hf——管道沿程水头损失,m;
f——摩阻系数;
l——管道长度,m;
Q——流量,m3/s;
d——管道内径,m;
m——流量指数,与沿程阻力系数有关;
b——管径指数,与沿程阻力系数有关;
S0——比阻,即单位管长、单位流量时的沿程水头损失。
比阻S0可用式(3-19)表示,即
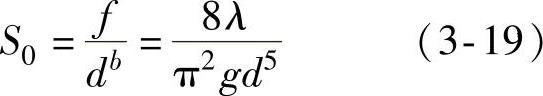
式中符号的意义同前,其中摩阻系数、流量指数和管径指数与管道材质和内壁糙度有关。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




