土的压缩性与软土固结试验

一、工作任务

通过软土固结试验知识的学习，学生应能够承担以下工作任务：

（1）掌握土的压缩性及压缩性指标的基本概念。

（2）掌握土的压缩性指标的简单计算。

（3）掌握地基最终沉降量的计算方法。

（4）掌握固结试验的操作步骤、数据收集及成果的整理分析。

二、相关配套知识

（一）土的压缩性

1.土体压缩的概念

土体在压力作用下体积减小的性质叫作土的压缩性。它反映了土中应力与其变形之间的关系，是土的基本力学性质之一。

土是由土粒及土粒间孔隙中的水和空气所组成的三相分散系，土体被压实后，其压缩变形一般包括：① 土粒发生相对移动，部分气体和水被挤出或溶解于孔隙水中，使孔隙体积减小；② 土粒本身被压缩；③ 土中水及封闭于土中的气体被压缩。一般情况下，后两者的体积减小量要远远小于孔隙体积的减少量，可忽略不计。因此，在讨论土的压缩性时，假定水和土粒都是不可压缩的，认为土体的压缩是由于土中水、气体所占据的孔隙体积减小造成的。

土粒的移动、靠拢及孔隙水的挤出都需要经历一定的时间才能够完成，因而土的压缩变形也需要持续一定时间才能趋于稳定。对于无黏性土，压缩过程所需的时间较短。对于饱和黏性土，由于水被挤出的速度较慢，压缩过程所需的时间就相当长，需几年甚至几十年才能压缩稳定。

2.土的压缩性指标

1）压缩试验

室内压缩试验的过程大致如下：先用金属环刀切取原状土样，然后将土样连同环刀一起放入压缩仪的圆筒形刚性容器内，土样上下两面均有透水石，使土样受压缩时，孔隙水可从上、下两面排出。通过传压活塞给土样施加压力，土样的变形用测微表（百分表）测量，如图 9-1 所示。在无侧向膨胀的条件下对土样分级施加竖向压力，一般土样加4级载荷，即50 kPa、100 kPa、200 kPa、400 kPa，根据每级载荷作用下土样的稳定变形量，可算出相应载荷作用下的孔隙比。因为在整个压缩过程中土样不能侧向膨胀，这种方法又称为侧限压缩试验。

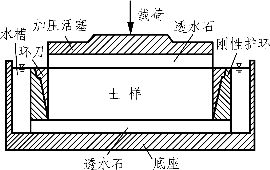
图9-1 压缩仪示意

如图 9-2 所示，设土样的原始高度为h0、土颗粒体积 Vs、土样的横断面面积，即压缩仪中取样环刀的横断面面积为A，此时土样的原始孔隙比e0为

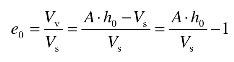
图9-2 压缩试验土样变形示意

土粒体积为

当压力增加到pi时，土样的稳定变形量为ΔSi、土样的高度 hi=h0 -ΔSi ，按照前述假定——土粒是不可压缩的，可知土粒的体积仍然是Vs，土样的孔隙比ei为

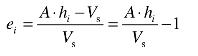
土粒体积为

由式（9-1）和（9-2）可得

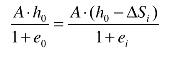
或

式中

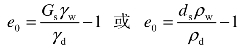
根据某级载荷下的稳定变形量为ΔSi，按式（9-4）即可求出该级载荷下的孔隙比ei，然后以横坐标表示压力p、纵坐标表示孔隙比e，可绘出e-p关系曲线，此曲线称为压缩曲线，如图9-3所示。

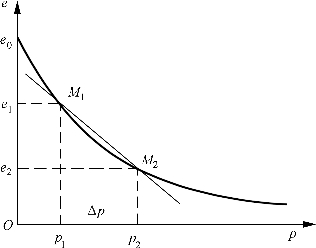
图9-3 e-p曲线

2）压缩系数

从如图 9-3 所示的压缩曲线可见，在侧限压缩条件下，孔隙比随着压应力的增加而逐渐减小。M1、M2为压缩曲线上的两点，其坐标为（ p1，e1）和（p2，e2），当压力从 p1增加至p2时，孔隙比由e1减小至e2，若压应力变化范围（Δp）不大，对应的曲线段 M1 M2近似地可用直线段来代替，直线段的斜率为

式（9-5）为土的压密定律，即在压力变化不大时，土中孔隙比的变化与所加压力的变化成正比。比例系数a称为压缩系数，它是反映土的压缩性质的重要指标。a值大，则在一定压力范围内孔隙比变化也大，土的压缩性就高。对同一种土而言，压缩曲线的斜率是变化的，当压力增加时，曲线斜率a减小。当然，不同土的压缩性不一样，压缩曲线也就不同。

在实际工程中，土的压力一般取 p1=0.1 MPa 到 p2=0.2 MPa 的变化范围确定土的压缩系数，并用a1—2表示，根据其大小作为评价地基土压缩性的指标：

低压缩性土 a1—2＜0.1 MPa -1

中压缩性土 0.1 MPa -1 ≤a1—2＜0.5 MPa -1

高压缩性土 a1—2 ≥0.5 MPa -1

【例9-1】 已知某土样的原始孔隙比e0=0.86，压缩试验前试样的原始高度为20 mm，当压力 p1=0.1 MPa 时，试样的总变形量为0.892；当压力为 p2=0.2 MPa 时，试样的总变形量为1.219，试求压缩系数a1-2，并判定土的压缩性。

解：利用式（9-4）可得

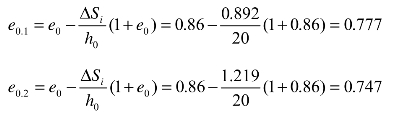
利用式（9-5）可得

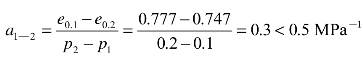
0.1 MPa－ 1＜ a1—2＜0.5 MPa －1，所以土样为中压缩性土。

3）压缩模量

土的压缩模量是指土在无侧向膨胀的条件下，土的竖向应力增量与竖向应变增量的比值，用符号Es表示。它与一般材料弹性模量的区别是：① 土在压缩试验时不能侧向膨胀，只能竖向压缩；② 土是非弹性体，当压力卸除后，不能完全恢复到原位置，除部分弹性变形外，还有相当部分是不可恢复的残余变形。

如图 9-4 所示，在压缩试验过程中，土样的压力从 p1增加至p2时，压应力增量为Δp=p2 -p1，土样的高度由h1减小至 h2，孔隙比由e1减小至e2。据式（9-3）有

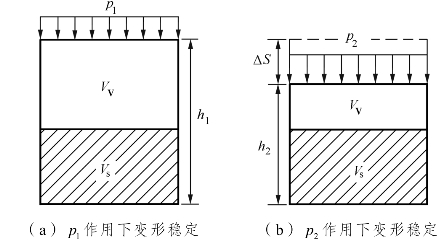
图9-4 压缩过程中土样变形示意

竖向应变增量为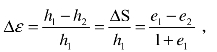由Es的定义及式（9-5）可得

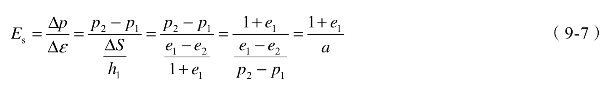
把式（9-7）代入式（9-6）可得

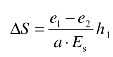
把式（9-5）代入上式可得

土的压缩模量Es是表示土的压缩性高低的又一个指标，上式表明了压缩模量Es与压缩系数a之间的关系：Es与a成反比，a越大，Es越小，土越软弱。与压缩系数a1—2相对应的压缩模量用Es1—2表示，它也可作为评价地基土压缩性的指标：一般 Es1—2 ＜4 MPa 属高压缩性土，Es1—2 =4～15 MPa 属中等压缩性土， Es1—2 ＞15 MPa 为低压缩性土。

4）变形模量

土的变形模量是指土体在无侧限条件下，土的竖向应力增量与竖向应变增量的比值，用符号E0表示。变形模量可由室内侧限压缩试验得到的压缩模量求得，也可通过静载荷试验（浅层土）、旁压或触探试验（深层土）确定。

（1）由室内试验测定的Es求E0。

根据材料力学原理，可以求出土的变形模量E0和压缩模量Es之间的理论关系

式中

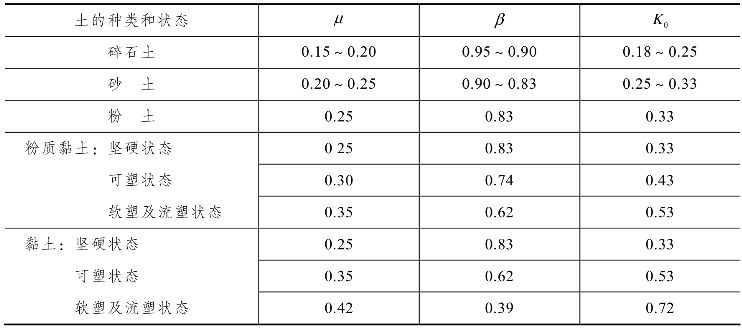
μ、β、K0的经验值见表9-1。

表9-1 μ、β、K0的经验值

实际上，室内与现场的试验条件是不同的，如室内压缩试验对土样的扰动较大、两者加荷速率也不对应、土的泊松比也不易精确测定。因此，要得到能较好地反映土的压缩性的指标，应在现场进行静载荷试验。

（2）由静载荷试验测定E0。

如图9-5所示，在准备修建基础的地点开挖基坑，并使坑底标高等于基底标高，在坑底上安置方形或圆形刚性承压板（承压面积0.25～1.0 m2），坑的宽度应不小于承压板宽度的 3倍。加载设备安置在承压板上面，一般由支柱、千斤顶、锚碇木桩和刚度足够大的横梁组成。用放在承压板上方的百分表量测地基变形，加载由小到大分级进行，每级增加的压力值视土质软硬程度而定，对较松软的土，一般为10～25 kPa；对较坚硬的土，一般按 50 kPa 的等级增加。每加一级载荷，必须等候一段时间，待沉降基本稳定时，再加下一级载荷。

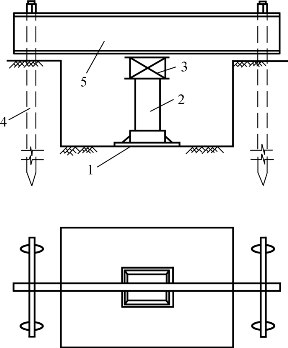
图9-5 静载荷试验装置示意

1—承压板；2—支柱；3—千斤顶；4—锚碇木桩；5—横梁。

在试验过程中，由逐级增加的载荷测定相应的承压板的稳定沉降量。根据试验结果，按一定比例以压力p为横坐标，稳定沉降量s为纵坐标，在直角坐标系中可绘出压力与沉降的关系曲线，即p-s关系曲线（图9-6）。

根据p-s关系曲线的初始段 0-pcr ，可求得板下1.5～2倍承压板边长或直径深度范围内土层的平均变形模量E0。在此阶段，承压板底下土体可视作均质各向同性的半空间弹性体，利用弹性理论求得地基土的变形模量为：

式中 E0——地基土的变形模量；

ω——与承压板形状和刚度有关的系数，方形板取0.88，圆形板取0.79；

μ——地基土的泊松比；

b——承压板宽度或直径；

p、s——初始段 0-pcr 上某点的压力值和沉降值。

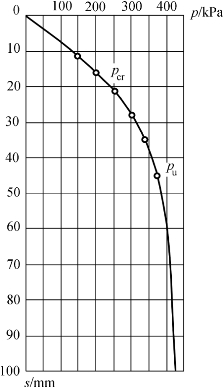
图9-6 静载荷试验的沉降曲线

按现场静载荷试验确定的土体变形模量E0比按 β· Es 的计算值更能反映土体压缩性质。只有土体为软土时，二者才比较接近，对于坚硬土E0可能是 β· Es 的数倍。因此，对于重要建筑物，最好采用现场载荷试验确定E0的值。

（二）地基的最终沉降量

地基的最终沉降量是指建筑物地基从开始变形一直到变形达到稳定时基础的总沉降量。目前计算基础沉降量的方法很多，本节只介绍分层总和法和规范法。

1.分层总和法

1）计算假定

（1）地基中的各薄层均只产生竖向压缩变形，无侧向膨胀。在沉降计算中，可以使用室内侧限压缩试验的成果，如压缩系数a、压缩模量Es和e-p曲线。

（2）按基础底面中心下的土柱所受附加应力进行基础沉降量计算。

（3）计算压缩层范围内的变形。沉降计算的深度在理论上应该计算至无穷大，但附加应力从基底开始随深度的增加而减小，到达一定深度后，由附加应力引起的土体压缩变形已经很小，可忽略不计，从基础底面到该深度之间的土层，就是压缩层。

2）计算步骤

（1）分层。

将基础底面以下地基土划分成若干水平薄层，分层的原则是：

① 不同土层的分界面应为分层面；② 地下水位面应为分层面；③ 每一分层的厚度不超过0.4b（b为矩形基础短边的宽度），应保证每个薄层内附加应力分布线近似于直线，以便较准确地求出各层内附加应力平均值，一般可采用上薄下厚的方法。

（2）计算自重应力。

计算基础底面中心下每一分层面处的自重应力 σcz(i)及每一分层的平均自重应力σczi=并在基础底面中心线左侧沿深度z绘制自重应力分布曲线。

（3）计算附加应力。

① 计算基底处的附加应力：

式中 p0——基底处的附加应力（kPa）；

p——基底压力（kPa）；

σcz ——基底处的自重应力（kPa）。

② 利用角点法计算基础底面中心下每一分层面处的附加应力σz(i)及每一分层的平均附加应力并在基础底面中心线右侧沿深度z绘制附加应力分布曲线。此时应该注意：附加应力应从基础底面算起。

（4）确定地基受压层深度。

随着深度的增加，附加应力值以及附加应力与自重应力的比值都是减小的，同时，在正常情况下，土的压缩性也常随着深度增加而降低，因此，在某一深度以下，由附加应力引起的压缩量将小到在实际应用中可以忽略不计的程度。

在实际工程计算中可采用基底以下某一深度zn作为基础的下限深度，计算沉降时，只需考虑地基沉降计算深度zn范围内的变形量。确定zn的条件是：对于一般土，取 σzn ≤ 0.2σczn ，对于软土，则取 σzn ≤ 0.1σczn 。

（5）计算各薄层的压缩量。

令 p1i =σczi 、p2i=p1i +Δpi=σczi +σzi ，从该薄层土的压缩曲线中由p1i和p2i分别查出e1i和e2i ，利用式（9-6）有：

（6）计算地基的最终沉降量。

将地基受压层深度zn范围内的压缩量相加即得：

2.规范法

《铁路桥涵地基和基础设计规范》（TB 10093—2017）推荐的基础总沉降量计算方法是单向压缩分层总和法的一种简化形式，它仍采用侧限压缩试验获得的压缩性指标，计算薄层的平均值附加应力时采用平均附加应力系数计算。地基沉降计算深度规定了相对变形为控制标准，提出了沉降经验修正系数，调整理论计算结果与基础实际沉降更加一致。

基础由于其底面以下受压土层zn压缩产生的总沉降量S可按下式计算：

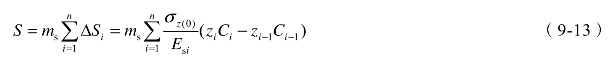
式中 S——基础的总沉降量（cm）。

n——基底以下地基沉降计算深度范围内按压缩模量划分的土层分层数目。

σz(0)——基础底面处的附加压应力（kPa）， σz(0) =σh -γh 。

σh——基底压应力（kPa），当时，hσ采用基底平均压应力；当时，hσ采用基底压应力图形中距最大应力点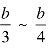处的压应力。

其中 b——基础的宽度（m）。

γ——土的容重（kN/m3）。

h——基底埋置深度（m），当基础受水流冲刷时，由一般冲刷线算起；当不受水流冲刷时，由天然地面算起，如位于挖方内，则由开挖后地面算起。

z——基底至计算土层顶面的距离。

zi 、zi-1——自基底至第i和第i-1薄层底面的距离（m）。地基沉降计算总深度zn的确定应符合下列要求：

Esi ——基础底面以下受压土层内第i薄层的压缩模量（kPa），根据压缩曲线按实际应力范围取值。

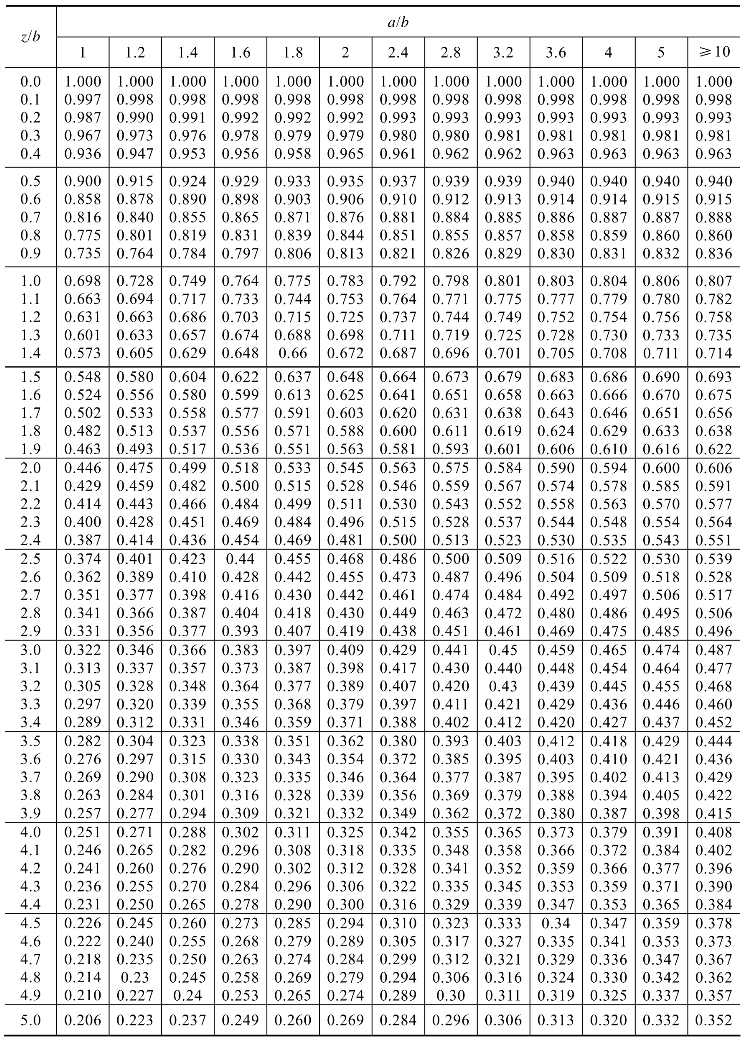
Ci 、Ci-1——基础底面至第i薄层底面范围内和至第i-1薄层底面范围内的平均附加应力系数（图9-7），可按表9-2查得。

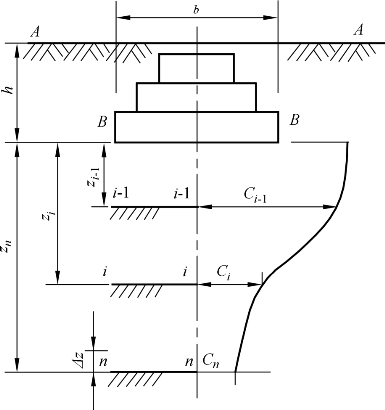
图9-7 基础沉降计算

A—A—地面；i—i—第i层底面；B—B—基础底面；n—n—第n层底面；i－1—i－1—第i－l层底面；C—平均附加应力系数C曲线。

表9-2 矩形面积上均布荷载作用下通过中心点竖线上的平均附加应力系数C

ms——沉降经验修正系数，可按表9-3采用，对于软土地基ms=1.3。

表9-3 沉降经验修正系数

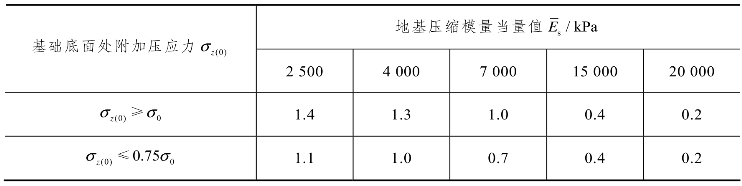
注：表中 σz(0) =σh -γh ， σh为基底压应力，近似地取基底压应力图形中距最大压应力点 b/3～b/4 处的压应力。σ0为基础底面处地基的基本承载力。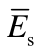为沉降计算总深度zn内地基压缩模量的当量值，应按下式确定：

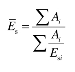
其中 Ai为第 i 层土平均附加应力系数沿该土层厚度的积分值，即第 i 层土的平均附加应力系数面积。

式中 ΔSi——计算深度范围内第i薄层土的沉降量；

ΔSn ——深度zn处向上取厚度为Δz（表9-4）的土层的沉降值。

表9-4 Δz的值

(www.xing528.com)

（三）地基沉降与时间的关系

1.有效应力原理

如图9-8（a）所示，在饱和土体中任意取一面积为A的水平截面a—a，作用于A上的应力σ由土体的重力、水压力及外荷载产生，称为总应力。总应力σ中的一部分由土颗粒间的接触面积来承担，称为有效应力，另外一部分由土体孔隙内的水来承担，称为孔隙水压力。

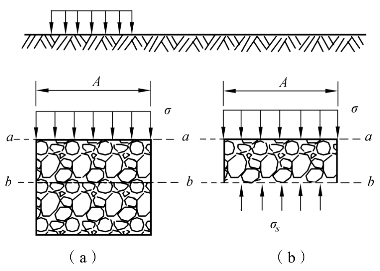
图9-8 有效应力原理

沿着b—b截面截取隔离体aabb，如图 9-8（b）所示，假设该截面沿着土颗粒间的接触面，土颗粒间接触面上作用的法向应力为 σs，各个土颗粒间的接触面积之和为 As，孔隙水压力为u，其相应的面积为 Aw。考虑土体的平衡条件有：

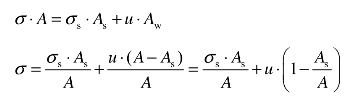
上式中的第一项是土颗粒间的接触压力在截面上的平均应力，称为土的有效应力，通常用σ′表示。由于颗粒间的接触面积 As很小，即于是上式可写成：

式（9-15）就是有效应力原理，由它可得到两个结论：一是土的有效应力等于总应力减去孔隙水压力；二是作用于骨架上的有效应力是影响土的变形和强度的决定因素。

土中任意点的孔隙水压力的大小在各个方向上都是相等的，它只能使土颗粒本身产生压缩（压缩量很微小，忽略不计），不能使土颗粒产生位移。只有土颗粒之间的有效应力作用，才会引起土颗粒的相对位移，使孔隙体积发生改变，土体发生压缩变形。

有效应力原理是土力学中的一个十分重要的原理，是土力学成为一门独立学科的重要标志。它是近代土力学的一个重要内容，古典土力学用总应力研究土的压缩性和抗剪强度，而现代土力学则用更符合实际的有效应力来分析解决问题。

2.饱和土体的渗压模型

饱和土体的孔隙中充满着水，在荷载作用下，只有挤出孔隙水，土体才能被压密，即土体产生压缩变形，这个过程叫作渗透固结。

饱和土体的渗透固结过程，可借助如图 9-9 所示的弹簧活塞力学模型来说明。在一个装满水的圆筒的上部安置一个带小孔的活塞，活塞与筒底之间安装一个弹簧，活塞重量及其与筒壁间的摩擦力不计。活塞上的小孔、弹簧和筒中水分别代表孔隙通道，土颗粒骨架和孔隙水。弹簧顶开始时与水面齐平。

这个模型中弹簧受力相当于饱和土体中土粒骨架受力，称为有效应力σ′；筒中水的受力相当于土中孔隙水受力，称为孔隙水压力u。饱和土体在附加压力作用下渗透固结的情况与上述模型受力后的变化情况很相似。

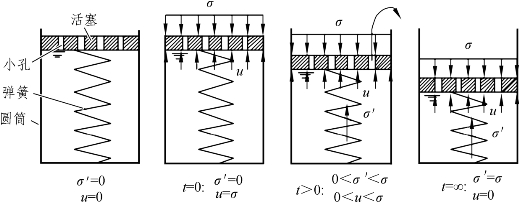
图9-9 饱和土体的渗透固结模型

在活塞顶面施加压力σ的瞬间，孔隙水尚未来得及从小孔排出，活塞没有下降，弹簧也未压缩变形。因此，弹簧不受力，压力σ完全由孔隙水承担，即：σ′=0，u=σ。

随着时间的增长，孔隙水不断地通过活塞上的小孔向外流出，筒中水的体积逐渐减小，活塞不断下降，弹簧逐渐压缩变形，其承担压力逐渐增大。在此期间，筒中水压力逐渐减小，但弹簧和水受力的总和始终不变，即：σ=σ′+ u 。此式就是土骨架和孔隙水的压力分担作用的数学表达式。

当时间足够长时，筒中水停止向外流出，孔隙水压力u=0，弹簧也停止压缩，压力σ全部转移到弹簧上，σ′=σ，渗透固结过程结束。

由此可见，饱和土体的渗透固结过程，就是土中的孔隙水压力消散并逐渐转移为有效应力的过程，此过程的任一时刻都有 σ=σ′+ u 。

3.单向渗透固结理论

在地基基础设计中，往往不仅需要知道地基的最终沉降量，有时还需要知道地基的整个沉降过程，这就需要了解沉降和时间的关系，即沉降过程中某一时间的沉降量或达到某固结度时需要的时间等，以便预先考虑建筑物有关部分之间的净空，考虑连接方法和施工顺序。对于已发生裂缝、倾斜的建筑物，也需要知道地基沉降与时间的关系，以便对比沉降计算值和实测值，来确定是否需要及时对地基进行处理。

在土体的渗透固结过程中，要使孔隙中的水通过非常细小的孔隙排出，需要经历一定的时间才行。这个时间的长短主要取决于土层排水距离、渗透系数和压缩系数的大小等因素。一般建筑物在施工期内完成的沉降量，对于砂土可认为其最终沉降量已基本完成，对于低压缩性黏性土可认为已完成后最终沉降量的 50%～80%，对于中压缩性黏性土可认为已完成20%～50%，对于高压缩性黏性土可认为已完成5%～20%。未完成的沉降量在建筑物建成后继续沉降，对于桥梁、房屋等的使用造成不利影响的正是地基的这种后期沉降。

在天然土层中，常遇到厚度不大的饱和软黏土层，当受到较大的均布荷载作用时，只要顶面或底面有透水层，则孔隙水主要沿竖向排出，可认为是单向固结情况。

要确定饱和黏性土层在渗透固结过程中任意时间的变形，通常采用太沙基提出的单向（一维）渗透固结理论进行计算。其假定条件为：① 土是均质、各向同性和完全饱和的；② 土粒和孔隙水都是不可压缩的；③ 土的压缩和孔隙水的挤出都只在竖直单向发生，土的固结速度取决于孔隙水的挤出速度；④ 土中水的渗流为层流，服从于达西定律；⑤ 在固结过程中，渗透系数k与压缩系数Es为常数；⑥ 外荷载是一次瞬时施加的，而且沿着土层深度呈现均匀分布。

如图9-10所示的土层情况属单向渗透固结，图中厚度为H的饱和黏土层的顶面是透水的，而底面是不透水的不可压缩层。该饱和黏土层在自重作用下已压缩稳定，在附加应力作用下发生固结。当该土层表面突然受到连续均布荷载p作用时，在土中引起的附加应力沿深度均匀分布，强度大小为p，如图9-10中bc所示。由于水只能从表面透水层排出，土层表面排水距离最短，底面排水距离最长，当排水开始后，土层表面的孔隙水压力立即降到零，而底面孔隙水压力降低很少。其他各层面处孔隙水压力则随深度减小而降低，变化情况如图中9-10的bd所示。随着时间增长，曲线形状将逐渐发生变化，如图中虚线所未。由此可见，土中有效应力和孔隙水压力分别是深度和时间的函数，即：

σ′= f(z,t )， u=F(z,t)

可见，当t=0时，bd与ae线重合， σ′= f(z,t )=0， u=F(z,t )=σz，即全部附加应力都由孔隙水承担；当t=∞时，bd与bc重合，σ ′= f(z,t )=σz ， u=F(z,t)=0，即全部附加应力都由土骨架承担。

在距离饱和土层顶面以下深度z处取一体积为 dxdydz微单元体，见图9-10，并结合上述假定条件可导出饱和黏性土的单向渗透固结微分方程：

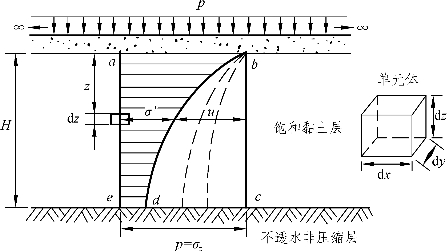
图9-10 饱和黏性土层的渗透固结

式中 Cv——土的固结系数，；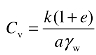

k——土的渗透系数；

e——土层固结过程的平均孔隙比；

a——土的压缩系数；

γw——水的重度， γw ≈ 10 kN/m3。

由图9-10所示的附加应力分布情况，可得初始条件为：

当t=0，0≤z≤H时， u=σz

当t=∞，0≤z≤H时，u=0

由土层顶面、底面的排水条件，可得边界条件为：

当0＜t＜∞，z=0时，u=0

当0＜t＜∞，z=H时，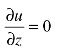

根据以上初始条件和边界条件，求解微分方程（9-16），得到孔隙水压力随时间t和深度z变化的函数关系式为：

式中 Tv——时间因数，。

p——附加应力，不随深度变化。

m——正整数， m= 1,3,5,7,…。

H——最大排水距离（m），当土层为单面排水时，H等于土层厚度；当土层为上下双面排水时，H等于土层厚度的一半。

在实际应用中，通常用到地基的固结度Ut这一指标，它是指地基在外荷载作用下，经历时间t产生的沉降量St与地基最终沉降量S的比值，其表达式为：

经历时间t产生的沉降量St取决于地基中的有效应力，有：

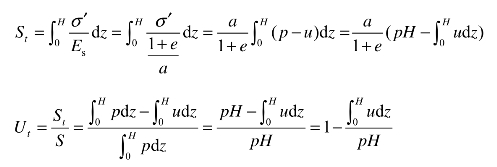
把式（9-17）代入上式得：

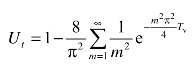
上述级数收敛速度很快，当 Ut ＞ 30%时，采用第一项已足够精确，上式成为：

从上式可以看出固结度度Ut是时间因数vT的函数，它与所加的附加应力无关。对不同的附加应力分布形态和排水条件，同样可导出相应的固结度公式。为便于应用，绘制出Ut与vT的关系曲线如图9-11所示，图中一共有10条曲线，由下而上分别是a=0，0.2，0.4，0.6，0.8，1，2.0，4.0，8.0，∞。其中，。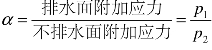

情况0：α=1，相当于基底面积很大而压缩土层较薄的情况；

情况1：α=0，相当于大面积新填土，因自重应力引起的固结；

情况2：α＜1，相当于自重应力作用下土层尚未固结完毕，又在其上施加荷载；

情况3：α=∞，相当于土层很厚，基底面积较小的情况；

情况4：α＞1，类似情况3，但不透水层面的附加应力大于零。

以上情况是单面排水。如果土层上、下都有排水砂层，则属于双面排水，其固结度均按情况0计算，但在时间因数中，应以代替H。

（四）软土固结试验

1.仪器设备

本试验应采用的仪器设备：

固结容器：由环刀、护环、透水板、加压上盖和水槽等组成，如图9-11所示。

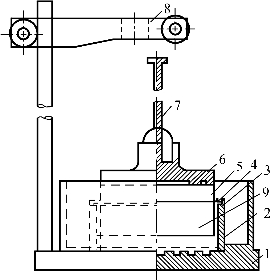
图9-11 固结容器示意

1—水槽；2—护环；3—环刀；4—导环；5—透水板；6—加压上盖；7—位移计导杆；8—位移计架；9—试样。

（1）环刀：内径为61.8 mm和79.8 mm，高度为20 mm。

（2）透水板：由透水石或不受腐蚀的金属材料制成，其渗透系数必须大于试样的渗透系数。顶部透水板的直径应小于环刀内径0.2～0.5 mm。

（3）加压设备：能垂直施加各级规定的压力，无冲击影响。

（4）变形量测设备：百分表量程10 mm，分度值为0.01 mm或准确度为全量程0.2% 的位移传感器。

（5）天平：称量500 g，分度值0.1 g；称量100 g，分度值0.01 g。

（6）其他：切土刀、钢丝锯、称量盒、烘箱、秒表等。

2.试验步骤

试验操作应按下列步骤进行：

（1）根据工程需要，切取原状土试样或制备给定密度与含水率的扰动土试样。

（2）在固结容器内放入护环、透水板、滤纸；将带有环刀的试样装入护环内，在试样上再放入滤纸、透水板、加压盖板，置于加压框架下；对准加压框架的中心，安装百分表或位移传感器。当试样为饱和土时，上、下透水板应事先浸水饱和；对非饱和状态的试样，透水板和滤纸的湿度应与试样湿度相接近。

（3）施加 1 kPa 的预压力，使试样与仪器上下各部件之间接触良好，将百分表或位移传感器调整到零位或测读初始值。

（4）记录初始读数后，卸除预压力，开始施加第一级压力，第一级压力的大小应根据土的软硬程度而定，可分别为12.5 kPa、25 kPa或50 kPa。

（5）饱和试样或工程上要求浸水的试样，在施加第一级压力后，立即向容器内注水，使试样在水下进行试验。非饱和试样，用湿棉纱围住加压盖板四周，以避免试验过程中水分的蒸发。

（6）加压等级一般为 12.5 kPa、25 kPa、50 kPa、100 kPa、200 kPa、400 kPa、800 kPa、1 600 kPa、3 200 kPa。最后一级的压力应大于上覆土层计算压力的100～200 kPa。

（7）需要测定先期固结压力时，加压率宜小于1.0，可采用0.5或0.25的加压率。最后一级压力应使e-lgp曲线的下段出现较长的直线段。

（8）当需测定沉降速率、固结系数时，加压后应按下列时间顺序测记量表读数：6 s、15 s、1 min、2 min15 s、4 min、6 min15 s、9 min、12 min15 s、16 min、20 min15 s、25 min、30 min15 s、36 min、42 min15 s、49 min、64 min、100 min、200 min、400 min及23 h、24 h直至稳定为止。

（9）当不需要测定沉降速率时，稳定标准为每级压力下固结 24 h。只测定压缩系数时，每级压力下的稳定标准为每小时试样的变形量不大于0.005 mm。

（10）当需作回弹试验时，可在某级压力下固结稳定后逐级卸荷，直到卸至第一级压力为止。每次卸荷后的回弹稳定标准与加压时相同，并测记每级压力及最后一级压力时的回弹稳定读数。

（11）试验结束后，迅速拆除仪器各部件，取出带环刀的试样，擦干试样两端和环刀壁上的水分，并测定整块试样试验后的含水率。

3.成果处理

试验结果应按下列公式计算及制图：

（1）初始孔隙比

式中 e0——初始孔隙比，计算至0.01；

ρs——颗粒密度（g/cm3）；

w0——试样初始含水率（%）；

ρ0——试样初始密度（g/cm3）。

（2）各级压力下固结稳定后的单位沉降量

式中 Si——单位沉降量（mm/m）；

∑ Δhi——在某级压力下，试样固结稳定后的总变形量（mm），等于该压力下固结稳定后的读数减去仪器变形量；

h0——试样的初始高度（mm）。

（3）第i级压力下固结稳定后的孔隙比

式中 ei——第i级压力下固结稳定后的孔隙比，计算至0.01；

hi——第i级压力下固结稳定后的高度（mm）。

（4）某一压力范围内的压缩系数

式中 av——某一压力范围内的压缩系数（MPa－1），计算至0.01 MPa－1；

ei+1——第i＋1级压力下固结稳定后的孔隙比；

pi ——第i级压力（kPa）；

pi+1——第i＋1级压力（kPa）。

（5）某一压力范围内的压缩模量和体积压缩系数

式中 Es——压缩模量（MPa），计算至0.1 MPa；

mv ——体积压缩系数（MPa－1），计算至0.01 MPa－1。

（6）压缩指数和回弹指数

式中 Cc——压缩指数，即e-lgp曲线直线段的斜率，计算至0.001；

Cs ——回弹指数，即回弹曲线上某一压力范围内的平均斜率，计算至0.001。

（7）以单位沉降量Si或孔隙比e为纵坐标，压力p为横坐标，绘制单位沉降量或孔隙比与压力的关系曲线，如图9-12所示。

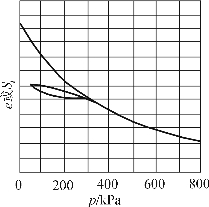
图9-12 e(Si)-p关系曲线

（8）以孔隙比e为纵坐标，lgp为横坐标，绘制e-lgp关系曲线，如图9-13所示。

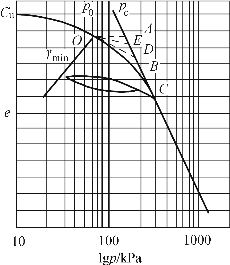
图9-13 e-lgp曲线求pc示意图

（9）原状土的先期固结压力pc的确定方法如图 9-13 所示，在e-lgp曲线上找出最小曲率半径Rmin点O，过O点作水平线OA，切线OB及∠AOB的角平分线OD，OD与曲线直线段C的延长线交于E点，对应于E点的压力即为该原状土的先期固结压力pc。

（10）固结系数Cv应按下列方法确定：

① 时间平方根法：

对某一级压力，以试样的变形 d（mm）为纵坐标，时间平方根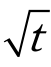（min）为横坐标，绘制d -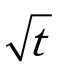曲线，如图 9-14 所示。延长d -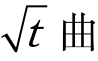线开始段的直线，交纵坐标轴于 ds（ds为理论零点）。过ds作另一直线，使其横坐标为前一直线横坐标的 1.15 倍，则后一直线与d -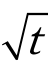曲线交点所对应的时间的平方即为试样固结度达 90% 所需的时间t90。该压力下的固结系数按下式计算

式中 Cv——固结系数（cm2/s），计算至0.01 cm2/s；

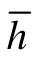——最大排水距离，等于某一压力下试样初始和终了高度的平均值之半（cm）；

t90——固结度达90% 所需的时间（s）。

② 时间对数法：

对某一级压力，以试样的变形d（mm）为纵坐标，时间对数lgt（min）为横坐标，绘制d -lgt 曲线，如图9-15所示。在d-lgt曲线的开始线段，选任一时间t1，相对应的变形量为d1，再取时间t2 =t1 /4，相对应的变形量为d2，则 2d2 -d1为d01。依次再取另一时间按此法求得d02、 d03、 d04等，取其平均值即为理论零点d0。延长d-lgt曲线中部的直线段和过曲线尾部数点作一切线的交点即为理论终点d100；则。对应于 d50的时间即为试样固结度达50% 所需的时间t50，该压力下的固结系数按下式计算

式中 t50——固结度达50% 所需的时间（s）。

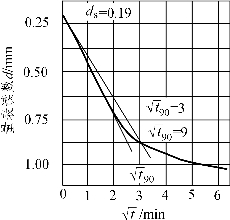
图9-14 时间平方根法求t90

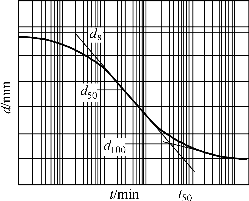
图9-15 时间对数法求t50

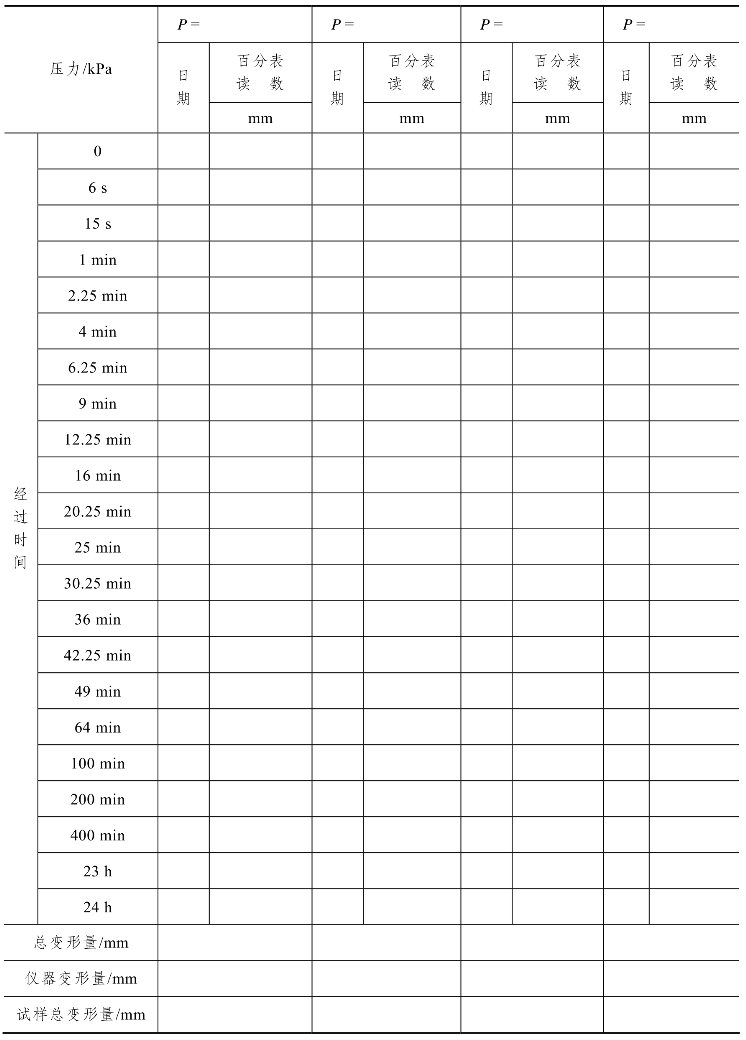
4.数据记录

记录格式应符合表9-5、表9-6的要求。

表9-5 标准固结试验记录（一）

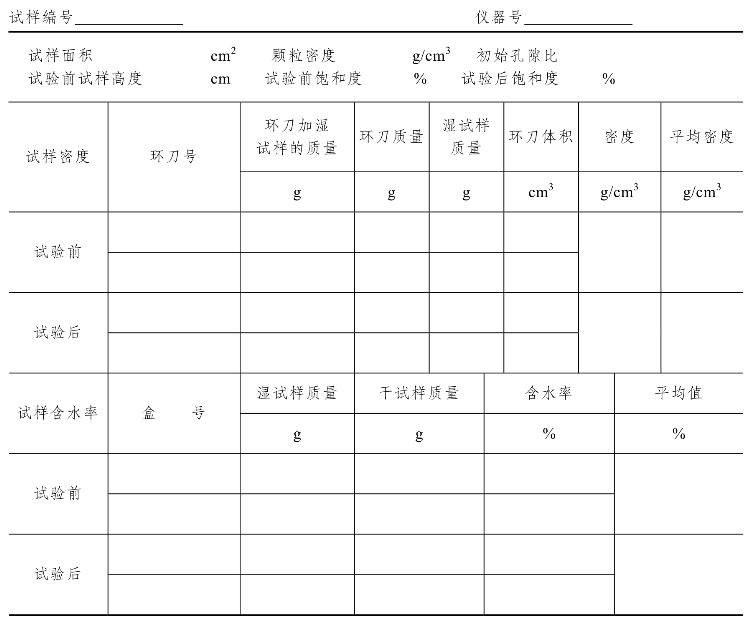
表9-6 标准固结试验记录（二）