
图19 14世纪zellige
通常理解伊斯兰选择抽象纹样是被迫的选择,好像是因为宗教禁止艺术家描绘现实中的形象,赛义德·J.阿巴斯认为这是“毫无根据并且完全错误的”。是伊斯兰文明在几何学中找到了对于其信仰的一种确认和一种系统,只不过在伊斯兰文化中对几何的理解和执行更为彻底而已。“这种系统使得艺术家们能够根据自然界本身的一种规律来拓展它们的创造力并进行无穷的探索。对于抽象的伊斯兰艺术转向及其以后的繁荣,既不是出于强迫,也不是由于责任,而是来自于选择”。[28]柏拉图也曾做了同样的选择:“我们每个人的头脑中都有一种能力,在被其他的追求破坏并弄瞎之后,这些(几何)学问会净化并重新点燃它。这种能力比任何眼睛都更值得保存,因为它是我们洞察真理的唯一器官。”
伊斯兰艺术之所以能够提供这种体验,是因为它对建构于几何和对称的探索。正如历代伊斯兰智者们所言:几何的主导性是至高无上的,宇宙的和谐唯有通过最纯粹完美的几何形式才能被真正体会到。对称的几何图样构成了艺术的主要部分,它自然而然地引出“对称和抽象”(图6)这两个人类大脑所能构想的最自然也最深刻的概念,并同时能把科学、艺术和自然完美地协调在一起。
几乎所有的人类文化都曾探讨过几何和对称,不过在伊斯兰文明中这种探索才真正开始体现出它的价值。赛义德·J.阿巴斯认为“这种艺术在14世纪中期达到巅峰,从而出现了像在西班牙纳斯里(Nasrid)王朝阿罕布拉宫那样灿烂辉煌的建筑”(见图9)。而组成这个建筑的,除了建筑结构,是把几何和伊本·穆格拉倡导的“匀称的脚本”发挥到极致的“勒里碣”。阿巴斯试图把伊斯兰的几何纹样与今天的数学联系起来,几何纹样的变化不是通过记忆而是通过使用计算机图形学和更高级的数学而获得。譬如多面体表面上的伊斯兰图样模型、代数曲面上的图样模型、非周期性图样模型、颜色对称、夸张对称、虚拟真实图样模型,以及非线性格子的使用,等等。这倒是为伊斯兰传统的复兴及其未来发展提供了一种激动人心的可能性。因为大多都会只从表面装饰,或者只与宗教等关联起来看待伊斯兰的几何图形,伊斯兰几何纹样与现代更高级的数学的联系完全没有被充分强调。
几何图样大量地出现在伊斯兰文化不同的材料上和其他不同种功能的物体上,不仅在现实生活的毛毯上和清真寺的布道台上,在建筑表面上更为突显。这些经常交织在一起的直线元素显示出游牧穆斯林居住帐篷和编织毛毯的起源和经验。“交织就是一切”(图19)引出另外一种伊斯兰图样特征,这是一种与“流动性”和“无限性”有关联的重复特征。用直线方格重复是伊斯兰图样中所使用的几何基础,这个特征可以很清楚地反映在陶瓷马赛克的重复上,陶瓷方块不断地重复着以至于无穷,空间由此而被最大限度地得以填充,与之相随的特征“对眼睛来说没有一个自然的聚焦点。当一个人观赏一幅宏大的图样模型的时候,它的眼睛会因为追随持续不断的线条,以及看到很多错综复杂的结构和关系而流动”[29]。
因为几何是中性的,所以如何定义摩洛哥风格的伊斯兰几何图样?在能被证明从10世纪到16世纪被用来装饰马格里布的建筑外表和其他艺术品的“勒里碣”图样上,可以总结出摩洛哥“勒里碣”几何纹样的大致特征:
星形形状:
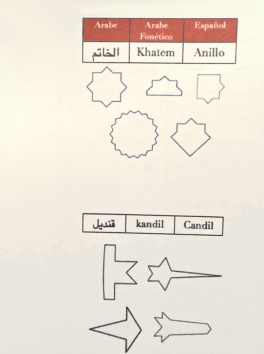
把一个圆对称分割成八角或把两个正方形交叉重叠,就会产生出了一个特殊的八角星形,这是一种很基础的“勒里碣”纹样策略,是伊斯兰图样模型里出现得最为普遍的形状。它的八角星形称为“苏莱曼的封印”。在“勒里碣”中出现的频率很高,而且“勒里碣”大量的基本星形纹样可以被看作是“khatem”的变体。khatem星形(图20)甚至代替摩洛哥对城市十字路口的理解,组成了摩洛哥城市中的街道交叉路口的基本交叉方式。以星形为中心,通过交叉点产生的多角星形,可以简单地通过瓷砖的块状复制来构建几何纹样模型。
方与圆的重叠与重复:
很多“勒里碣”纹样先以一个方格结构的重复开始。当这个方格被复制时就会产生出一些隐含的方格。最常被用到的有斜角方格(从正方形斜切中所建构的)、方形和长方形。根据几何计算,六个等边三角形结合形成一个正六边形,同样长方形也可以被分为正三角形或者菱形,以此类推,在“勒里碣”中复杂的图样有时候会使用更为复杂的方格结构(图21)。
 (https://www.xing528.com)
(https://www.xing528.com)
图20 名称
对称:
对称引起我们称之为愉悦情感的生理性唤醒。为了生存,大脑必须能够识别安全与稳定,既然生存是生理本能最高的考虑,耐久性的东西都具有对称性,那么大脑就会对对称性进行自我适应使之产生对对称的审美。对称是所有文化艺术的基础,但对称却特别赋予伊斯兰艺术整体性以特殊的内容,也得以使“勒里碣”的几何纹样的重复对称有了美学和哲学的基础。对称概念并不仅限于几何,但有关模型与对称更为抽象的概念,却完全可以通过几何来介入。在“勒里碣”传统形式上,伊斯兰几何图样直接来源于希腊的几何学。但几何在伊斯兰文化中嵌入的价值远不在于仅仅掌握数学概念,更为重要的是转化出对于井然有序的空间直觉和“勒里碣”的审美形成。
复制:
在分析“勒里碣”的对称美学时,复制是一种基本的节奏,把单元旋转和反射是唯一可以制作出与原型完全一致的方法,而使用平移和滑移两种转换方法可以假定无限制延伸的单元。
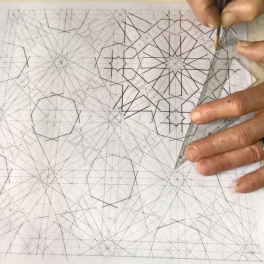
图21 几何图案计算

图22 现代风格
物体经过一个或多个等距转换,其所占据的空间位置保持不变,这个物体转换就是数学上的对称概念。把单元的每一个点以完全相同的数量沿着同一个方向移动,叫作平移。平移与反射相结合的移动叫作滑移。因为需要复制与建筑空间的场域结合而产生出丰富的量,“勒里碣”赋予复制这个概念以深刻的含义。在纹样形状转换时,通过平移、旋转、反射、滑移等转换,看似拼贴后还保持着平面感,但“勒里碣”的几何碎块得以最大限度地使几何的复制概念立体实践化,而非画在表面的二维平面模拟。同样是几何纹样装饰,这也构成了摩洛哥的“勒里碣”不同于土耳其瓷砖上绘制几何花纹的画面感的平面装饰(图22)。
混合后的几何纹样形成了上千种纹样,仅仅是复制的结构,阿罕布拉宫就储备了几乎已知所有的伊斯兰图样,堪称伊斯兰纹样的图书馆。几何纹样结构被今天的数学家归纳为有17种群,阿罕布拉宫先是发现了11种不同类型的几何纹样群,吸引了学者们的注意力。20世纪80年代,格拉纳达大学的戈麦兹(R.Gomez)和马德里大学的J.蒙泰斯诺斯(J Montesinos)甚至在阿罕布拉宫的纹样中找到了全部17种纹样群,在600年前就能完成今天穷计算机之力计算出的几何结构,这是伊斯兰艺术和几何的智慧和美学的结合的完美物证。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




