电梯静阻转矩影响及电动机功率计算

电梯的轿厢和对重构成垂直运动的势能性负载，其合力F，忽略曳引钢丝绳、补偿链和移动电缆的影响就是势能性负载阻力，如图3⁃3所示。

轿厢和对重在上下运动时，各自的导靴与导轨之间存在摩擦。因此，当轿厢上升时，负载静阻力为

F_lu＝（1＋f₁）（G₁＋G₂）－（1－f₂）G₃ （3⁃4）

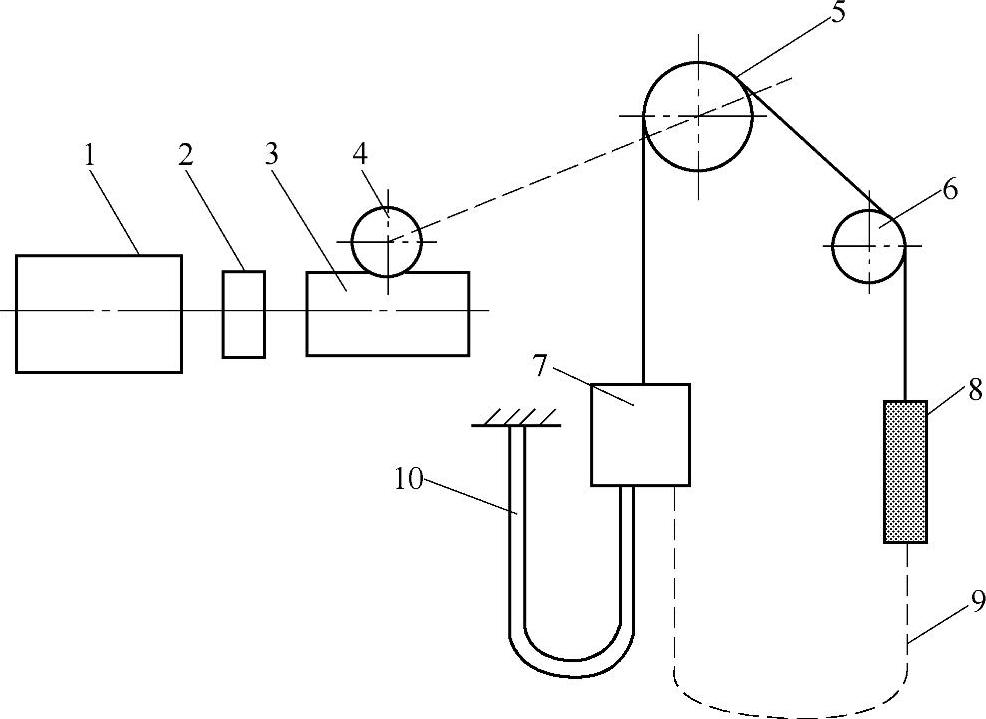
图3⁃2 电梯的运动系统

1—曳引电动机 2—联轴器与制动轮 3—蜗杆 4—蜗轮 5—曳引轮 6—导向轮 7—轿厢 8—对重 9—补偿链 10—移动电缆

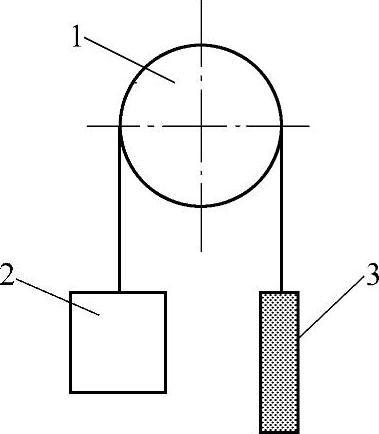
图3⁃3 阻力计算示意图

1—曳引轮 2—轿厢 3—对重

当轿厢下降时，负载静阻力为

F_ld＝（1－f₂）G₃－（1＋f₁）（G₁＋G₂） （3⁃5）

式中 G₁——轿厢自重；

G₂——轿厢载重；

G₃——对重重量；

f₁——轿厢导靴与导轨的摩擦阻力系数；

f₂——对重导靴与导轨的摩擦阻力系数。

忽略导向轮的摩擦阻力影响，若曳引轮半径为R，当轿厢上升时，则曳引轮轴上的静阻转矩为

T_l′_u＝F_luR＝［（1＋f₁）（G₁＋G₂）－（1－f₂）G₃］R （3⁃6）

当轿厢下降时，曳引轮轴上的静阻转矩为

T_l′_d＝F_ldR＝[（1－f₂）G₃－（1＋f₁）（G₁＋G₂）]R （3⁃7）

当蜗杆为主动旋转而蜗轮为从动旋转时，按照能量守恒定律，此时电动机轴的输出功率应等于曳引轮的输出功率与蜗轮蜗杆的传动损耗的和。在轿厢满载上升时，电动机轴输出功率为

则(www.xing528.com)

式中 T_l′_u——折算到电动机轴上的负载转矩；

Ω——电动机轴角速度；

Ω′——曳引轮角速度；

j——传动速比；

η1——蜗杆为主动旋转而蜗轮为从动旋转时，蜗轮蜗杆的总传动效率。在轿厢空载下降时，电动机轴输出功率为

则

式中η2——蜗轮为主动旋转而蜗杆为从动旋转时，蜗轮蜗杆的总传动效率。

转矩经过折算之后，系统就可等效为电动机与负载的同轴系统了。由式（3⁃6）和式（3⁃7）可知，折算转矩T_lu和T_ld此时均为正值，即均为阻转矩，电动机工作在电动状态，同时负担传动损耗，如图3⁃4和图3⁃5所示。

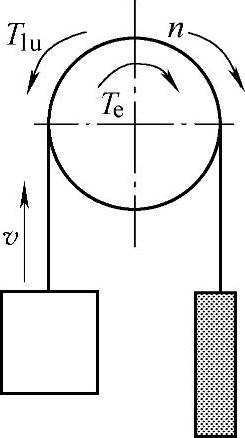
图3⁃4 轿厢满载上升

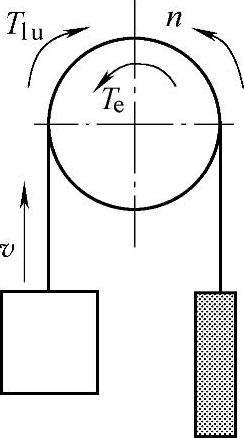
图3⁃5 轿厢空载下降

根据式（3⁃6）和式（3⁃7）可知，此时折算转矩T_lu和T_ld均为负值，表明负载阻转矩为驱动转矩。由于势能性负载的作用，使曳引电动机处于发电制动状态，由势能性负载负担传动损耗，如图3⁃6和图3⁃7所示。

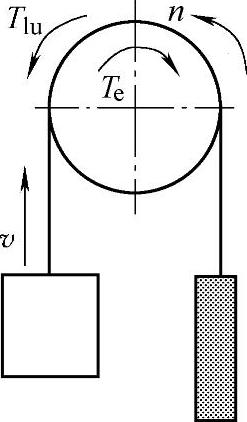
图3⁃6 轿厢满载下降

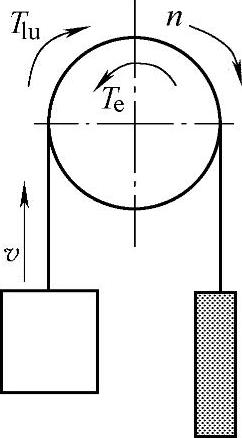
图3⁃7 轿厢空载上升

在无齿传动电梯中，由于电动机与曳引轮同轴，所以无须进行转矩折算，曳引轮上的静阻转矩就是电动机轴上的静阻转矩。