公交专用道乘客感知服务水平评估方法

1）估算方法一的理论推导

以W表示等车时间，w表示任意给定时间，FW（w）表示等车时间分布即W小于等于w的概率，fW（w）表示等车时间的概率密度函数，H表示车头时距。

等车时间的概率密度函数fW（w）为［135］：

fW（w）＝［1-FH（w）］／E（H）　（6-18）

式中，FH（w）为车头时距H小于w的概率；E（H）为保证概率密度曲线下的面积为1而出现在公式中。

式（6-18）中，1-FH（w）为车头时距H大于等于w的概率，因此，式（6-18）表明等车时间是w的概率密度与车头时距大于等于w的概率成正比。

有n个车头时距，从小到大依次命名为H1，H2，H3，…，Hn。让给定时间w＝H1，n个车头时距中，车头时距大于等于H1的概率为则等车时间是H1的概率密度为fW（H1）以此类推，等车时间是H2，H3，…，Hn的概率密度分别为fW（H2）＝因此，等车时间是Hi的概率密度为：

式中，i＝1，2，…，n。

考虑到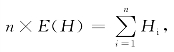故等车时间是Hi的概率密度fW（Hi）可表达为：(www.xing528.com)

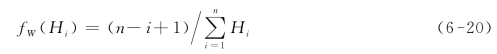
式（6-20）给出了给定时间w等于Hi时的等车时间概率密度。根据式（6-18），当给定时间w小于H1时，fW（w）＝fW（H1）；当w介于Hi与Hi＋1时，i＝1，2，…，n-1，fW（w）＝fW（Hi＋1）；当w大于Hn时，fW（w）＝0。因此，等车时间概率密度曲线如图6-2所示。

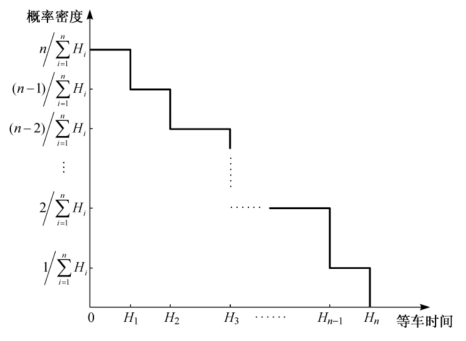
图6-2　乘客等车时间的概率密度曲线

等车时间分布FW（w）为等车时间W小于等于w的概率，其值等于概率密度曲线图中w左侧对应的概率密度曲线与坐标轴围成的矩形的面积。让w＝H1，FW（H1）等于图6-2中长为H1，高为的矩形的面积，即同理，FW（H2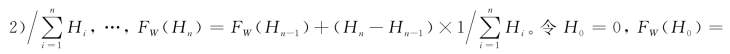）＝0，取给定时间w＝Hi，等车时间分布FW（w）为：

2）估算方法一的应用

基于n个给定的车头时距，通过分析等车时间为给定车头时距的概率密度，推导出等车时间分布的一种估算方法，如式（6-21）所示。该方法的计算结果为等车时间小于等于给定车头时距的概率，等车时间小于等于其他值的概率或者某累积概率对应的等车时间可通过线性插值得到。

应用该方法计算等车时间分布时，用表格呈现计算过程。让第一列表示序号i，从0开始；第二列表示车头时距Hi，其从小到大排列；第三列表示前后车头时距之差Hi-Hi-1；第四列表示第五列表示等车时间分布FW（Hi）。

通过线性插值，从等车时间分布中找出累积概率95%对应的等车时间，即为95%位等车时间；然后根据式（6-16）计算平均等车时间；二者作差即可计算出潜在等车时间。