构建乘客满意度估计模型拟定的解释变量有乘客出行特征和乘客个人属性，出行特征包括到站时间、潜在等车时间、停靠站设施水平、车内时间、车内拥挤度；乘客个人属性包括性别、年龄、受教育程度、职业、出行目的、有无私家车。其中，到站时间、潜在等车时间、车内时间、车内拥挤度为连续型变量；停靠站设施水平、性别、有无私家车为二分类变量；年龄、受教育程度、职业、出行目的为多分类变量。对于停靠站设施水平，以1表示候车停靠站有座椅、遮挡物、实时到站信息等设施，0表示候车停靠站没有这些设施。对于性别，以1表示女性，0表示男性。对于有无私家车，以1表示有，0表示没有。
考虑到变量太多不利于建模，且多分类变量某些类别的乘客满意度差异不显著，本章将多分类变量调查时所分的类别进行适当合并，重新分类以便于建模。对于年龄，调查时分为6～19岁、20～29岁、30～39岁、40～49岁、50～59岁和大于60岁6类。乘客满意度差异性检验发现，6～19岁和40～49岁、大于60岁的乘客满意度有显著差异。因此，本章将年龄重新分为6～29岁、30～39岁、40～59岁和大于60岁4类。对于受教育程度，调查时分为初中及以下、高中、大专、大学本科、硕士及以上5类。乘客满意度差异性检验发现，初中及以下与高中的乘客满意度没有显著差异。因此，本章将其合并，受教育程度被重新分为高中及以下、大专、大学本科、硕士及以上4类。职业调查时被分为公务员和教师、公司职员、学生、个体、家务和其他6类。回收的有效问卷中，家务的样本比例很低，仅占1.59%，本章将其归入其他类别，重点研究公务员和教师、公司职员、学生和个体的乘客满意度。出行目的调查时被分为上班、公务、购物娱乐、访友、上学和返程，本章将上班、公务、上学和返程合并，购物娱乐和访友合并，分为工作出行和娱乐出行2类。出行目的变为二分类变量，以1表示娱乐出行，0表示工作出行。
建模时对于多分类变量的处理方法为设置哑变量（也称虚拟变量），如果一个多分类变量有m个类别，则需要建立m-1个哑变量，被省略的类别称为参照类，一般把样本数最多的类别作为参照类［121，129-130］。作以上处理的原因是当引入m个变量时，回归方程将没有唯一解。由穷举与互斥原则规定，知道m-1个变量的值，就可推出第m个变量的值［130］。参照类虽然无法引入回归方程，但在解释结果时却非常重要，它被作为其他变量与之比较的基础。
对于年龄，设置3个哑变量，age1（30～39岁）、age2（40～59岁）和age3（＞60岁），6～29岁作为参照类。如果一个乘客的年龄处于6～29岁，则age1＝age2＝age3＝0。对于受教育程度，设置3个哑变量，edu1（高中及以下）、edu2（大专）、edu3（硕士及以上），本科为参照类。如果一个乘客的受教育程度为本科，则edu1＝edu2＝edu3＝0。对于职业，设置4个哑变量，ocu1（公务员和教师）、ocu2（学生）、ocu3（个体）、ocu4（其他），公司职员为参照类。如果一个乘客的职业为公司职员，则ocu1＝ocu2＝ocu3＝ocu4＝0。哑变量的含义及取值如表6-1所示。
表6-1 乘客满意度估计模型的哑变量名称、含义及取值
根据上述对多分类变量的处理，构建乘客满意度的有序Logistic回归模型时，解释变量有到站时间、潜在等车时间、车内时间、车内拥挤度、停靠站设施水平、性别、有无私家车、出行目的、age1、age2、age3、edu1、edu2、edu3、ocu1、ocu2、ocu3和ocu4。反应变量为乘客满意度，有非常满意、满意、不满意、非常不满意4个级别，分别以1表示非常满意、2表示满意、3表示不满意、4表示非常不满意，因此，反应变量的取值分别为1、2、3、4。将乘客满意度问卷调查回收的有效样本按照反应变量与解释变量的含义编码后，即可用于有序Logistic回归。
采用SAS软件进行有序Logistic回归，SAS语句为［120］：
Proc Logistic；（运行Logistic回归）(www.xing528.com)
Model反应变量＝解释变量；（指定反应变量和解释变量，并指定建立二者模型）
Output out＝xxxx；（指定输出数据集名称）
Predprobs＝（i）；（指定输出观测数据属于特定类别的概率）
Proc print data＝xxxx；（打印输出数据集）
Run；
SAS软件按照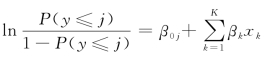
建模，因此，公交专用道乘客满意度有序Logistic回归模型的拟定形式为：
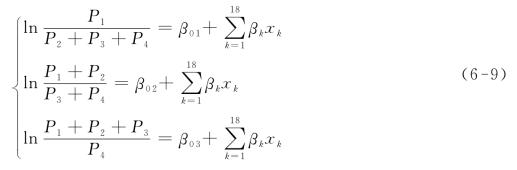
式中，P1表示乘客满意度为非常满意的概率；P2表示乘客满意度为满意的概率；P3表示乘客满意度为不满意的概率；P4表示乘客满意度为非常不满意的概率；xk表示到站时间、潜在等车时间、车内时间、车内拥挤度、停靠站设施水平、性别、有无私家车、出行目的、age1、age2、age3、edu1、edu2、edu3、ocu1、ocu2、ocu3和ocu4，k＝1，2，…，18；β01、β02、β03分别表示截距1、截距2和截距3，为待估计参数；βk表示xk的系数，为待估计参数。
3个累积对数发生比分子为满意程度的概率，如果一个变量使得累积对数发生比增大，则使得满意的概率增加，反之亦然。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
