公交运行延误与服务量关系分析

根据公交专用道仿真模型的输出数据，对单位公交专用道延误与服务交通量的关系进行研究。由于事先不明确二者的关系，故以线性、对数、二次、复合、幂、增长、指数等多种方程进行拟合。

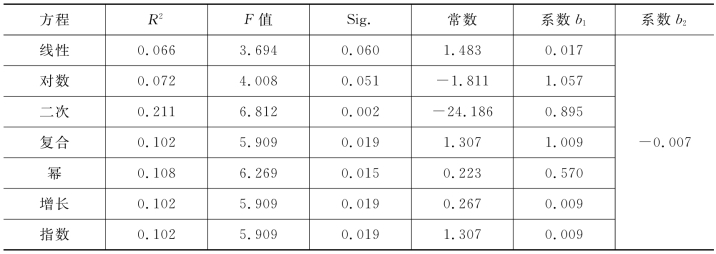
对于普通公交专用道，其单位公交专用道延误与服务交通量的多种方程拟合情况如表4-22所示。拟合情况很不理想，多种方程的R2均很低，说明单位公交专用道延误和服务交通量的相关性比较低，难以建立二者间的二元模型。从理论上来说，随着服务交通量的增加，单位公交专用道延误应呈现增加的趋势。但仿真时，服务交通量从20辆／h变化到100辆／h，相应的延误值变化很不明显。在普通公交专用道的停靠站，公交车可以超车，这样尽管流量增加，但不会显著影响公交车离站，从而导致上述现象的发生。

表4-22　普通公交专用道延误与服务交通量的多种方程拟合情况

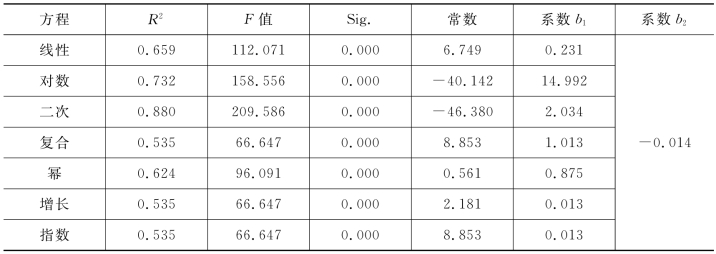
对于快速公交专用道，其单位公交专用道延误与服务交通量的多种方程拟合情况如表4-23所示。线性、对数、二次、幂4种方程的拟合程度较好，其中，二次方程的拟合程度最好，R2达0.88。说明单位公交专用道延误与服务交通量的相关性较高，可建立二者的二元模型。

表4-23　快速公交专用道延误与服务交通量的多种方程拟合情况

对于快速公交专用道，单位公交专用道延误与服务交通量的二次模型为：(www.xing528.com)

D0＝-0.014Q2＋2.034Q-46.380 R2＝0.88　（4-11）

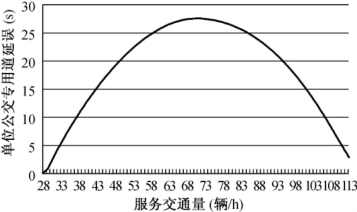
图4-6　快速公交专用道延误与服务交通量的二次曲线

式中，D0表示单位公交专用道延误（s）；Q表示服务交通量（辆／h）；模型适用范围：服务交通量介于30～120辆／h。

从单位公交专用道延误与服务交通量的二次模型可以看出，随着服务交通量的增加，延误呈现先上升后下降的趋势；在每小时的服务交通量为70～80辆时，延误处于峰值，如图4-6所示。

对于快速公交专用道，考虑到二次模型的局限性与线性模型描述问题的简单性，亦建立单位公交专用道延误与服务交通量的线性模型：

D0＝0.231Q＋6.749 R2＝0.659　（4-12）

式中，D0、Q的含义同上。