公交专用道乘客服务水平评估方法

国内外通常根据专家经验来界定服务水平分级，主观性较强［109-111］。本节试图采用具有理论基础的方法研究公交专用道的车辆运行服务水平分级问题。

4.1.2.1　因子评点法

因子评点法以评价指标服从正态分布为基础，以评价指标的均值和标准差划分服务水平分级。国外通常将服务水平分为A、B、C、D、E、F六级，因子评点法论述了划分为六级时的分级方法。具体步骤为［83］：

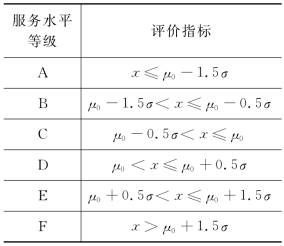
表4-2　因子评点法服务水平分级

（1）计算评价指标x的均值μ0与标准差σ。

（2）评价指标的正态分布检验。推荐的方法为：首先进行频次分析，绘制次数分布曲线，以从直观上观察评价指标是否服从正态分布；然后进行正态分布检验如K-S检验，以定量分析评价指标是否服从正态分布。

（3）如果评价指标服从正态分布，则以μ0作为C级的上限值，以μ0-1.5σ、μ0-0.5σ、μ0＋0.5σ、μ0＋1.5σ作为A级、B级、D级、E级的上限值。

因此，因子评点法确定的服务水平分级如表4-2所示。

因子评点法实质上是根据各级服务水平的期望概率确定评价指标的临界值。根据正态分布的分布函数，μ0-1.5σ的累积概率为7%，μ0-0.5σ的累积概率为31%，μ0的累积概率为50%，μ0＋0.5σ的累积概率为69%，μ0＋1.5σ的累积概率为93%。因此，A级、B级、C级、D级、E级、F级的概率分别为7%、24%、19%、19%、24%、7%，如图4-1所示。对因子评点法进行逆向分析，发现其思路为：首先明确各级服务水平的期望概率；然后确定各级服务水平评价指标临界值的累积概率；然后从评价指标的分布函数中找出累积概率值，即为评价指标的临界值。

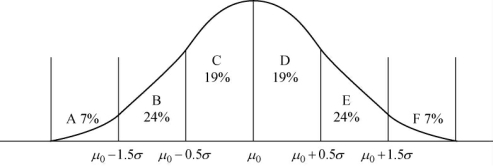
图4-1　因子评点法的各级服务水平概率

表4-3　因子评点法拟定的车辆运行服务水平分级

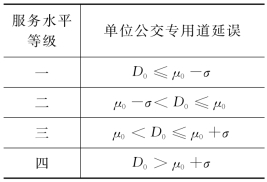
将公交专用道车辆运行服务水平分为四级，考虑到实际中一级和四级出现的可能性较小，而大多为二级和三级，因此，假定将一级、二级、三级、四级的概率指定为15%、35%、35%、15%。相应地，各级服务水平临界值的累积概率分别为15%，50%，85%。因此，根据因子评点法划分公交专用道车辆运行服务水平分级时，临界值分别为μ0-σ、μ0、μ0＋σ，拟定的服务水平分级如表4-3所示。

4.1.2.2　本书提出的服务水平分级方法

受因子评点法的启发，本书提出了更为一般化的服务水平分级方法。该方法不要求评价指标服从正态分布，但要求用于服务水平分级的评价指标样本要尽可能大。该方法适合于评价指标值愈小，服务水平等级愈高的分级问题。具体步骤为：

（1）对评价指标x进行频次分析，分析其累积分布或者绘制累积分布曲线。

（2）根据实际情况指定各级服务水平的期望概率。例如，将服务水平分为四级，指定各级的期望概率分别为p1、p2、p3、p4，且p1＋p2＋p3＋p4＝1。

（3）根据各级服务水平的期望概率确定其临界值的累积概率。以x1、x2、x3表示服务水平分为四级时的临界值，则x1的累积概率F（x1）＝p1，x2的累积概率F（x2）＝p1＋p2，x3的累积概率F（x3）＝p1＋p2＋p3。

（4）从评价指标的累积分布或者累积分布曲线中找出累积概率值，即为各级服务水平的临界值。

4.1.2.3　K均值聚类

聚类分析是指按照对象的某些属性，将物理或抽象对象的集合分为由类似的对象组成的多个类，使同类中的对象具有较高的相似度，而不同类中的对象差别较大。聚类分析是重要的数据挖掘技术之一，已经被广泛地应用到诸多领域中，如金融数据分类、空间数据处理、模式识别、卫星图像分析和医学图像的自动检测。在大量的聚类算法中，K均值聚类和模糊C均值聚类是基于划分的聚类算法，需事先确定聚类数目。

服务水平分级问题可视为服务水平评价指标的聚类问题，使相似的评价指标样本尽可能地归为一类，而将不相似的评价指标样本尽量划分到不同类中。由于事先确定了服务水平的等级数目，因此本书采用K均值聚类和模糊C均值聚类研究公交专用道的车辆运行服务水平分级问题，并将聚类中心作为各级服务水平评价指标的中值。

K均值聚类的核心思想为：把n个数据点xj（j＝1，2，…，n）分为k个类Gi（i＝1，2，…，k），求每类的聚类中心ci，使得目标函数达到最小。以d（xj-ci）表示Gi中数据点xj与其聚类中心ci的距离，则目标函数可定义为［112］：

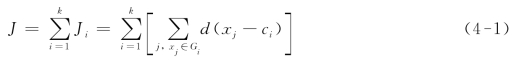
式中，是Gi内的目标函数，Ji的值依赖于Gi的几何特性与ci的位置。(www.xing528.com)

为简单起见，通常用欧几里德距离作为距离指标，因此d（xj-ci）＝｜｜xj-ci｜｜2。

划分过的类用隶属矩阵U来定义，其为k×n的二维矩阵。如果第j个数据点xj属于Gi，则U中的元素uij为1；否则，uij为0。一旦确定了聚类中心ci，可导出使目标函数式（4-1）最小的uij［113］：

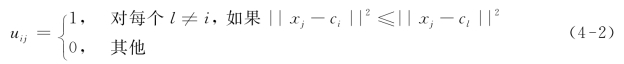
式（4-2）表明如果ci是距xj最近的聚类中心，那么xj属于Gi。由于一个数据点只能属于一个类，因此隶属矩阵U具有如下性质：。

K均值聚类先任意选择k个数据点作为初始类中心，然后计算每个数据点与各个类中心的距离，并将其赋给最近的类，更新类中心，不断重复此过程直到目标函数收敛，确定最终聚类中心ci和隶属矩阵U。具体执行过程为［114］：

（1）初始化聚类中心ci（i＝1，2，…，k）；

（2）用式（4-2）确定隶属矩阵U；

（3）根据式（4-1）计算目标函数，如果它小于事先给定的阈值，或相对上次迭代的目标函数值的改变量小于某个阈值，则算法停止；

（4）修正聚类中心，返回步骤（2）。

4.1.2.4　模糊C均值聚类

K均值聚类对于数据的划分是硬性的，即用0或者1表示数据点是否属于某类。模糊C均值聚类（简称FCM）对K均值聚类进行了改进，是一种柔性的模糊划分，即用值在［0，1］间的隶属度表示数据点属于某个类的程度［115-118］。

FCM把n个数据点xj（j＝1，2，…，n）分为C个模糊类，并求每类的聚类中心，使得目标函数达到最小。FCM的隶属矩阵U是一个C×n的二维矩阵，允许有值在［0，1］间的元素。不过，由于归一化规定，一个数据点的隶属度的和总等于1：

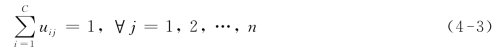
FCM的目标函数是式（4-1）的一般化形式，即［116］：

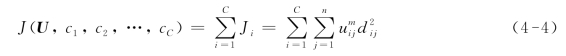
式中，uij介于［0，1］之间；ci为模糊类i的聚类中心；dij＝｜｜xj-ci｜｜，为第i个聚类中心与第j个数据点间的欧几里德距离；m∈［1，＋∞）是一个加权指数。

构造如下新的目标函数，可求得使目标函数式（4-4）达到最小的必要条件［117］：

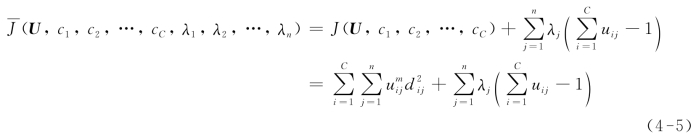
式中，λj（j＝1，2，…，n）是式（4-3）的n个约束式的拉格朗日乘子。

对所有输入参量求导，使得式（4-4）达到最小的必要条件为［118］：

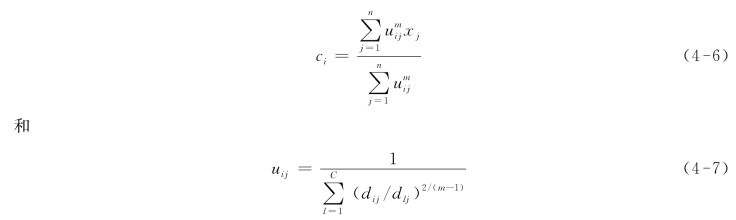
FCM按照下列步骤进行简单的迭代，直到目标函数收敛，确定最终的聚类中心ci和隶属矩阵U［115-118］。然后依据隶属矩阵，按照模糊集合中的最大隶属原则确定每个数据点的归类。

（1）用值在［0，1］间的随机数初始化隶属矩阵，使其满足式（4-3）中的约束条件；

（2）用式（4-6）计算C个聚类中心；

（3）根据式（4-4）计算目标函数，如果它小于事先给定的阈值，或相对上次迭代的目标函数值的改变量小于某个阈值，则算法停止；

（4）用式（4-7）计算新的隶属矩阵，返回步骤（2）。