本书建立的停靠站延误估算模型含有一个未知参数θ，它的取值需根据实地调查数据进行估计。本书通过理论推导建立了停靠站延误估算模型，模型的准确性需根据实地调查数据进行验证。因此，进行了公交专用道停靠站实地调查，以对参数进行估计、模型进行验证。参数估计是指根据实际延误和解释变量反推参数θ的值。模型验证是指比较实际延误和模型预测延误，模型预测延误根据解释变量和参数θ计算得到。
3.2.8.1 停靠站实地调查目的
停靠站实地调查的目的有两方面：一方面是调查实际延误；另一方面是调查模型中的解释变量包括到达率、停靠时间、泊位数及信号参数。延误调查和理论建模是独立的，为了方便从理论上推导延误的估算模型，将公交车在停靠站的等待过程抽象为3种情形。但在开展调查时，无需根据这3种情形设计调查方案或者试图分别调查这3种情形下的延误，而是要根据延误的定义设计调查方案，并尽可能地调查实际的延误，以和模型预测的延误进行对比。
3.2.8.2 停靠站实地调查方案与数据处理方法
停靠站延误被定义为公交车由于等待进站、等待前车离去和等待绿灯而在停靠站经历的平均等待时间。调查延误即要调查等待进站、等待前车离去和等待绿灯的等待时间。到达率是指单位时间内到达停靠站的公交车数量，因此，要记录每一辆到达停靠站的公交车以计算到达率。单泊位通行能力可通过停靠时间进行计算，也可根据现有的通行能力计算方法进行计算。考虑到实地调查可记录每辆车的实际停靠时间，因此，通过停靠时间来计算单泊位通行能力。停靠时间指公交车从开始减速到离开停靠站所花费的时间，减速进站时间和加速出站时间包含在停靠时间内。减速进站时间和加速出站时间为处于某范围的定值，为了简化调查，对其单独调查。将实地调查分为主调查和辅助调查。主调查为：记录调查时段内每辆到站公交车的停在站外时刻t1、停在车位时刻t2、完成上下客时刻t3、开始启动离站时刻t4。辅助调查为：观测数十辆车的减速进站时间和加速出站时间，计算它们的均值作为本次调查的减速进站时间ta和加速出站时间tc；观测数十辆车的行驶站区长度所用时间，计算它们的均值作为本次调查的行驶站区长度所用时间t5。辅助调查在主调查结束后或开始前进行。需要说明的是：t5实际上是指公交车从站外排队位置行驶到站内停车位置所用的时间，站外排队位置到站内停车位置的距离对于不同车而略有不同，本书统一将其取为站区长度，相应地，t5便为行驶站区长度所用的时间。
完成上下客时刻由于驾驶习惯的差异而不统一，在此对其作统一规定以减小不必要的误差。公交车在完成上下客后，如果不被阻挡，则驾驶员立即关车门并开始启动离站。此时，完成上下客时刻为开始关车门时刻。公交车完成上下客后，如果被阻挡，有些驾驶员会立即关车门，有些驾驶员不会立即关车门，而是在开始启动前关车门，因为在等待过程中可能还会有乘客登车。此时，完成上下客时刻不再是开始关车门时刻。因此，统一将不再有乘客连续上下时刻作为完成上下客时刻。
参数估计和模型验证所需的实际延误、到达率、单泊位通行能力根据主调查和辅助调查数据计算得到。首先计算每辆车的实际延误和停靠时间。每辆车的实际延误Ds＝（t2-t1-t5）＋（t4-t3），其中，t2-t1-t5为等待进站时间，t4-t3为等待前车离去和等待绿灯时间；每辆车的停靠时间T＝ta＋（t4-t1）＋tc。然后将10min作为一个计算单位（以t2为准），计算平均实际延误、到达率、单泊位通行能力。计算10min内所有到达车辆的实际延误的均值即为平均实际延误
；统计10min内到达的公交车数量n0，则到达率λ＝6×n0；计算10min内所有到达车辆的停靠时间的均值即为平均停靠时间
，则单泊位通行能力μ＝3 600／
。计算出调查时段内所有计算单位的平均实际延误、到达率和单泊位通行能力后，即可进行参数估计和模型验证。
3.2.8.3 停靠站实地调查的实施
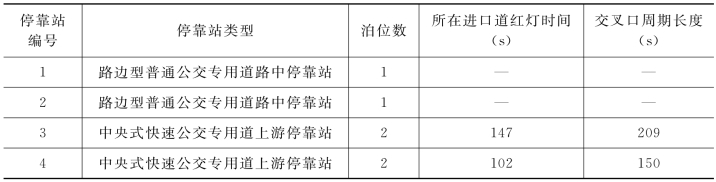
本书选取南京和常州的4个公交专用道停靠站进行实地调查，普通公交专用道和快速公交专用道各占2个。表3-1显示了所选停靠站的基本参数信息。调查于2013年4月11日（9：00～15：00）和4月12日（9：00～18：00）实施。有2名调查员参与调查，1个停靠站的调查由1名调查员负责。
表3-1 实地调查所选停靠站的基本参数
3.2.8.4 参数估计
本书建立了路边型普通公交专用道上游停靠站、路中停靠站、下游停靠站的延误估算模型，中央式快速公交专用道上游停靠站、路中停靠站、下游停靠站的延误估算模型。由于建模思路的一致性，仅以路边型普通公交专用道路中停靠站和中央式快速公交专用道上游停靠站的延误估算模型为例进行参数估计和模型验证，即对式（3-25）和式（3-24）进行参数估计和模型验证。
参数估计即根据实际延误和实际的解释变量取值对模型中的未知参数θ进行估计。θ表示由于公交车完成服务而被前车或红灯阻挡导致站外排队公交车排队时间波动的比率。对于路边型普通公交专用道路中停靠站，由于不存在公交车被前车或红灯阻挡的现象，模型中未含有参数θ。因此，仅对中央式快速公交专用道上游停靠站的延误估算模型即式（3-24）进行参数估计。(www.xing528.com)
本书采用最小二乘法进行参数估计，θ的值指定为0～1，以0.001为步长变化，参数估计的MATLAB代码见附录A。式（3-24）的参数估计采用3号停靠站的33组数据进行，每组数据包括到达率、单泊位通行能力、泊位数、红灯时间和周期长度和对应的实际延误。根据最小二乘法和所用数据，θ的估计值为0.467。说明对于所选停靠站的延误，0.467可产生最小的误差。也说明由于公交车完成服务而被前车或红灯阻挡导致站外公交车排队时间波动的比率为0.467，这符合实际情况。3号停靠站的红灯时间与周期长度的比值为0.7，从理论上讲公交车服务完被红灯阻挡的概率达70%。实地调查显示被红灯阻挡的概率高于该值，因为被红灯阻挡会进一步导致被前车阻挡，而被前车阻挡也会引发被红灯阻挡。被红灯阻挡和被前车阻挡相互作用，从而使得由于该现象导致的排队时间波动比率较高。
3.2.8.5 模型验证
模型验证即比较实际延误与模型预测延误以评价模型的准确性。对于路边型普通公交专用道路中停靠站，将解释变量取值代入到式（3-25）中即可计算出预测延误。对于中央式快速公交专用道上游停靠站，将解释变量取值和θ值（0.467）代入到式（3-24）中即可计算出预测延误。模型验证的MATLAB代码见附录B和附录C。
采用两种方式比较实际延误与模型预测延误，首先对实际延误和预测延误进行T检验，从统计上分析二者有无显著差异；然后将实际延误和预测延误作差，计算相对误差率。相对误差率是指实际延误和预测延误的差与实际延误的比值。
路边型普通公交专用道路中停靠站的延误估算模型式（3-25）的验证采用1号停靠站和2号停靠站的30组数据。实际延误和预测延误的T检验结果如表3-2所示，从表中可见，实际延误和预测延误没有显著差异，说明从统计角度讲，式（3-25）可用于该类停靠站延误的预测。验证所用数据的到达率、单泊位通行能力、实际延误、预测延误和相对误差率如表3-3所示。将每组数据的相对误差率绝对值求均值后，得到模型的平均相对误差率为31.71%，即式（3-25）的准确率为68.29%。
表3-2 路中停靠站延误估算模型的T检验结果
表3-3 路中停靠站延误估算模型的相对误差率
中央式快速公交专用道上游停靠站的延误估算模型式（3-24）的验证采用4号停靠站的34组数据。实际延误和预测延误的T检验结果如表3-4所示，从表中可见，实际延误和预测延误没有显著差异，说明从统计角度讲，式（3-24）可用于该类停靠站延误的预测。验证所用数据的到达率、单泊位通行能力、实际延误、预测延误和相对误差率如表3-5所示。将每组数据的相对误差率绝对值求均值后，得到模型的平均相对误差率为18.68%，即式（3-24）的准确率为81.32%。
表3-4 上游停靠站延误估算模型的T检验结果
表3-5 上游停靠站延误估算模型的相对误差率
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
