M/M/s模型中的排队长度和排队时间是随机变量。标准差可表达随机变量的波动量。让σ(Lq)表示排队长度的标准差,σ(Wq)表示排队时间的标准差。排队长度和排队时间的波动源于公交车到达情况的变动和停靠时间的变动。“完成服务的车辆打算出站,但是被前车或红灯阻挡,以至于继续占用泊位”这种现象增加了被占泊位的停靠时间,引起停靠时间变动,进而会导致排队长度和排队时间的波动。也就是说,这种现象是导致排队长度和排队时间波动的原因之一。记θ为由于这种现象导致的排队时间波动的比率,则θσ(Wq)为由于这种现象导致的排队时间波动量。这种现象会导致站外排队的公交车继续排队,进而产生额外等待时间,则θσ(Wq)即为该额外等待时间。因此,情形b下的转移进站阻挡延误等于情形b出现的概率Pb乘以θσ(Wq)。
3.2.4.1 排队时间标准差
以M/M/s(s>1)模型为例推导排队时间标准差的计算公式。推导的思路为:首先推导排队长度的方差及标准差,然后根据李太勒公式,得到排队时间的标准差。
根据随机变量方差的定义[100],可知排队长度的方差为:
![]()
根据随机变量函数的期望[100],即“对于任意离散型随机变量X,若Y=f(X),且P(X=xi)=Pi,i=1,2,…,∞,则![]() 将式(3-2)代入到
将式(3-2)代入到![]() 可表达为:
可表达为:
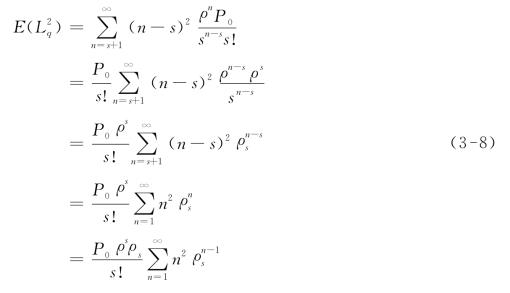
代数转换后,![]() 可表达为:
可表达为:
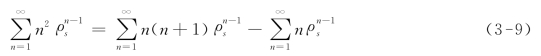
根据常用的幂级数公式[101],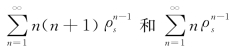 分别为:
分别为:
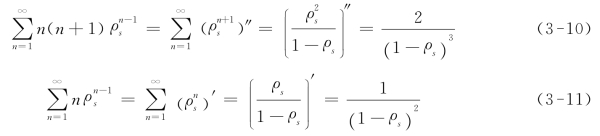
综合式(3-9)~式(3-11)后得到![]() 的表达式:
的表达式:

综合式(3-8)和式(3-12)后得到E(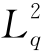 )的表达式:
)的表达式:

根据式(3-4)、式(3-7)和式(3-13),得到排队长度的方差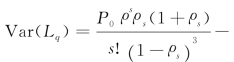
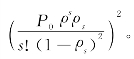 因此,排队长度的标准差
因此,排队长度的标准差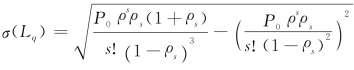 。
。
根据李太勒公式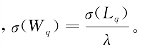 因此,对于M/M/s(s>1)模型来说,排队时间标准差
因此,对于M/M/s(s>1)模型来说,排队时间标准差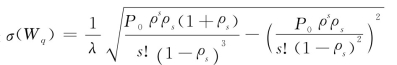 。
。
采用相同的方法可推导出M/M/1模型的排队时间标准差
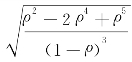 。
。
因此,M/M/s模型的排队时间标准差如式(3-14)所示。
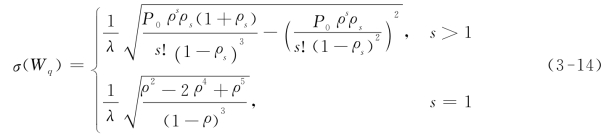 (https://www.xing528.com)
(https://www.xing528.com)
3.2.4.2 情形b出现的概率
(1)路边型普通公交专用道上游停靠站情形b出现的概率
在路边型普通公交专用道的上游停靠站,公交车可利用相邻车道超车,因此,完成服务的车辆不会被前车阻挡,只可能被下游交叉口的红灯阻挡。相应地,情形b变为:完成服务的车辆打算出站,但是被红灯阻挡,以至于继续占用泊位,从而导致站外排队的公交车继续排队。
以tr表示上游停靠站所在交叉口进口道的红灯时间,C表示交叉口的周期长度。完成服务的车辆被红灯阻挡的概率为![]() 考虑到只有当停靠站公交车数量大于泊位数即有排队车辆时,情形b才可能出现。因此,情形b出现的概率如式(3-15)所示。
考虑到只有当停靠站公交车数量大于泊位数即有排队车辆时,情形b才可能出现。因此,情形b出现的概率如式(3-15)所示。
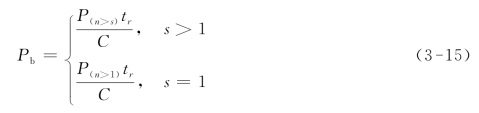
(2)中央式快速公交专用道上游停靠站情形b出现的概率
中央式快速公交专用道的停靠站可布设在专用道的右侧即靠近社会车道一侧,也可布设在专用道的左侧即靠近中央分隔带一侧。布设在右侧时,公交车在停靠站无法超车。布设在左侧时,往往会设置隔离栏以与社会车道分隔,公交车也不可超车。因此,公交车在中央式快速公交专用道的停靠站不可以超车。
在中央式快速公交专用道的上游停靠站,完成服务的车辆既可能被前车阻挡,又可能被红灯阻挡。情形b仍为:完成服务的车辆打算出站,但是被前车或红灯阻挡,以至于继续占用泊位,从而导致站外排队的公交车继续排队。下面分别推导完成服务的车辆被前车和被红灯阻挡而导致站外排队的公交车继续排队的概率。
![]()
图3-6 n>s的公交车在停靠站服务过程
对于s=1的停靠站,不存在完成服务的车辆被前车阻挡的现象。对于s>1的停靠站,情形b下停靠站的公交车数量大于s,即所有泊位被占用。此时,公交车在停靠站的服务过程如图3-6所示。如果泊位2的公交车先完成服务,则被泊位1的公交车阻挡。如果泊位3的先完成,则被泊位2的阻挡。也就是说,如果泊位i(i=2,3,…,s)的公交车先完成服务,总会出现完成服务的车辆被前车阻挡的现象。当且仅当公交车按占用泊位顺序完成服务时,即泊位1的公交车先完成,依次泊位2的公交车完成,…,泊位s的公交车完成,不会出现该现象。公交车按占用泊位顺序完成服务的概率等于![]() 因此,出现完成服务的车辆被前车阻挡的概率为
因此,出现完成服务的车辆被前车阻挡的概率为![]() 相应地,情形b中,完成服务的车辆被前车阻挡而导致站外排队的公交车继续排队的概率为
相应地,情形b中,完成服务的车辆被前车阻挡而导致站外排队的公交车继续排队的概率为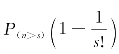 。
。
完成服务的车辆被红灯阻挡的概率亦为![]() 相应地,情形b中,完成服务的车辆被红灯阻挡而导致站外排队的公交车继续排队的概率为
相应地,情形b中,完成服务的车辆被红灯阻挡而导致站外排队的公交车继续排队的概率为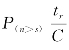 。
。
将上述两类概率相加即为情形b出现的概率,如式(3-16)所示。
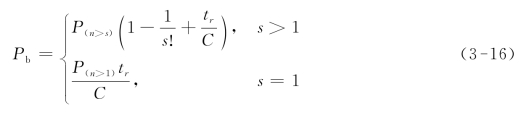
3.2.4.3 转移进站阻挡延误的估算公式
转移进站阻挡延误等于情形b出现的概率乘以θσ(Wq)。因此,根据式(3-14)和式(3-15)得到路边型普通公交专用道上游停靠站的转移进站阻挡延误,如式(3-17)所示。

根据式(3-14)和式(3-16)得到中央式快速公交专用道上游停靠站的转移进站阻挡延误,如式(3-18)所示。
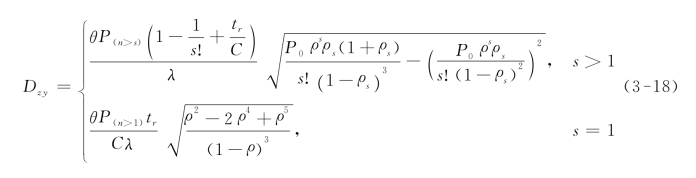
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




