车辆电磁兼容基础-能量流及传输

电磁场是一种物质，并且具有能量。例如，人们日常生活中使用的微波炉正是利用微波的能量给食品加热的。赫兹的辐射实验证明了电磁场是能量的携带者。时变电场、磁场都要随时间变化，空间各点的电场能量密度、磁场能量密度也要随时间变化。所以，电磁能量按一定的分布形式储存于空间，并随着电磁场的运动变化在空间传输，形成电磁能流。表达时变电磁场中能量守恒与转换关系的定理称为坡印廷定理，该定理由英国物理学家坡印廷在1884年初提出，它可由麦克斯韦方程直接导出为

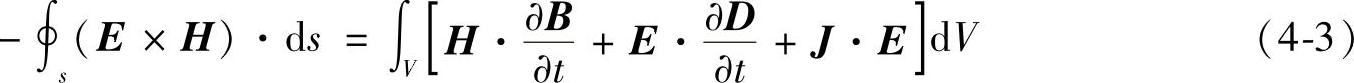
式（4-3）为适合任意媒质的坡印廷定理，实质上，坡印廷定理是能量守恒定律在电场问题中的具体表现。

利用矢量函数求导公式

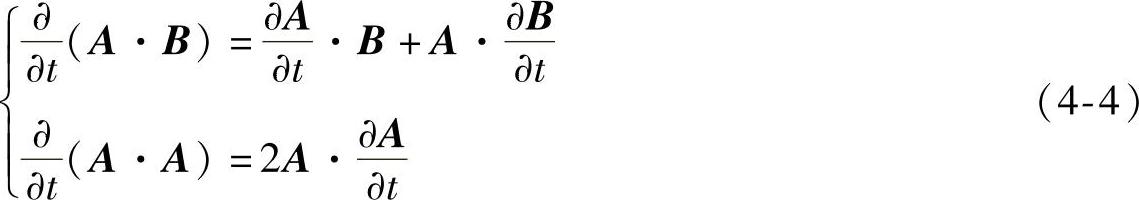
在线性、均匀、各向同性的媒质中，有

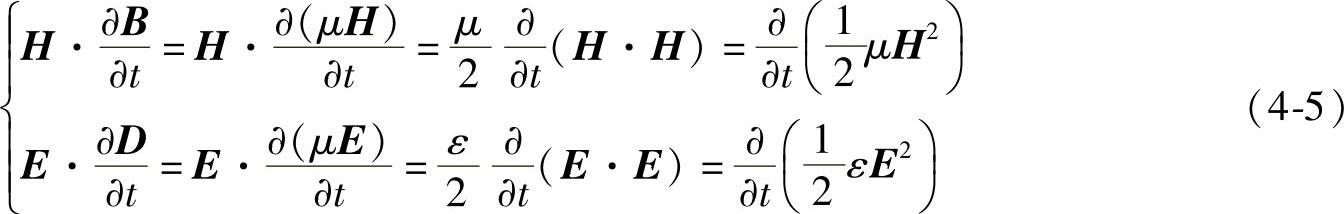
又注意到，电场强度E的大小与其能量密度ω_e的关系为

同样，磁场H的大小与其能量密度ω_m的关系为

(www.xing528.com)

观察矢量积E×H，它具有功率密度，单位为W/m²，称为坡印廷矢量，它表示单位面积的瞬时功率流，方向与包含E和H的平面垂直，用矢量S表示，即

S=E×H （4-8）

于是坡印廷定理可以写为如下形式

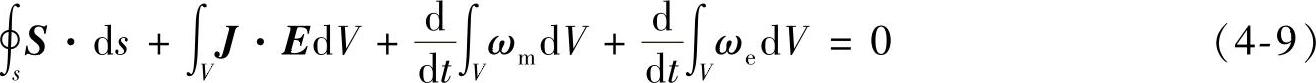
式中，第一项是一个在封闭面上进行的面积分，显然这个积分表示单位时间内从体积V内穿出封闭面向外流失的能量；第二项表示能量的损耗；后面两项分别表示磁场储能和电场储能的变化率。

从一个表面积为A的密封面向外的能量为

对于短线天线产生的远场区域，电场和磁场都被极化且同相。但在近场，很难看出结果是什么，因为电场存在两个分量，E_r×H_φ的方向不是从偶极子径向向外。因此，在近场区内的装置会遭受来自非轴向的能量传入。图4-8所示为电偶极子周围的能量流。

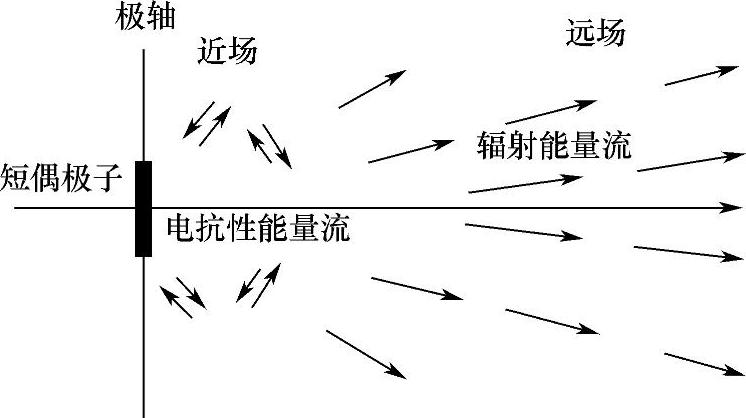
图4-8 电偶极子周围的辐射能量流