1.输入阻抗
终端接负载的传输线如图2-40所示。根据欧姆定律,定义传输线上任一点的电压与电流之比为该点(沿负载端)的输入阻抗。
由前述可知,对于无损耗线,α=0时,γ=jβ,则该点的阻抗为
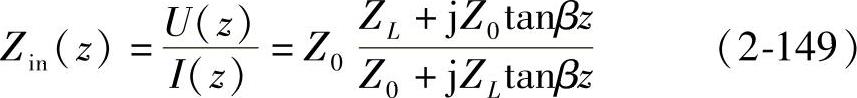
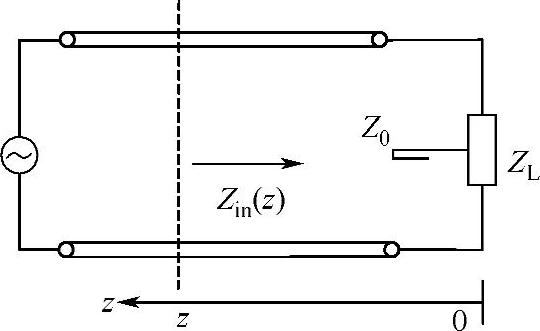
图2-40 终端接负载的传输线
由式(2-149)可知,均匀无耗传输线上任意一点的输入阻抗与负载阻抗ZL、特性阻抗Z0及距终端的位置z有关,一般为复数,故不宜直接测量,而且随位置的变化具有周期性,时间每增加λ/2,Zin重复出现一次,即

下面对几种特殊情况下的输入阻抗进行讨论:
(1)终端短路 当ZL=0时,由式(2-149)得
Zins=jZ0tanβz (2-151)
由此可见,终端短路的无损耗传输线的输入阻抗为纯电抗,其性质和大小随z的变化而发生改变,如图2-41所示。
z=0:Zins=0 串联谐振
0<z<λ/4:tanβz>0 呈感性
z=λ/4:Zins→∞ 并联谐振
λ/4<z<λ/2:tanβz<0 呈容性
z=λ/2:Zins=0 串联谐振(https://www.xing528.com)
线长每增加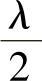 ,输入阻抗的性质重复一次。
,输入阻抗的性质重复一次。
(2)终端开路 当ZL→∞时,由式(2-149)得
Zino=-jZ0cotβz (2-152)
这时输入阻抗仍为纯电抗,可以是电感性的,也可以是电容性的,视βz的值而定。图2-42给出了Zino随z的变化曲线。比较图2-41和图2-42可见,z处的开路线输入阻抗等于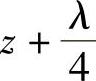 处的短路线的输入阻抗,即
处的短路线的输入阻抗,即

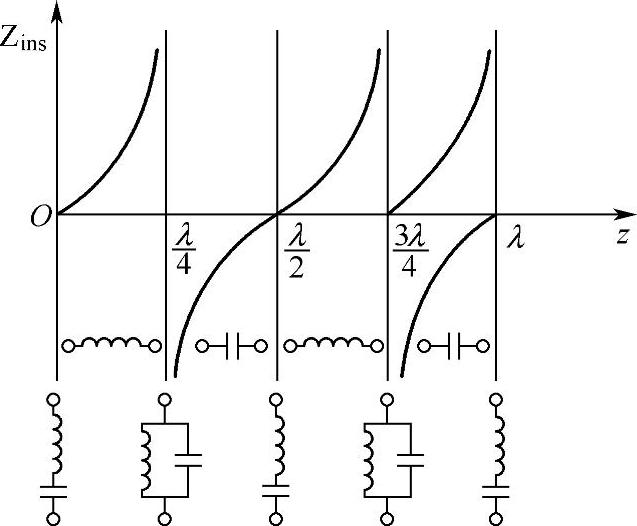
图2-41 终端短路线的输入阻抗
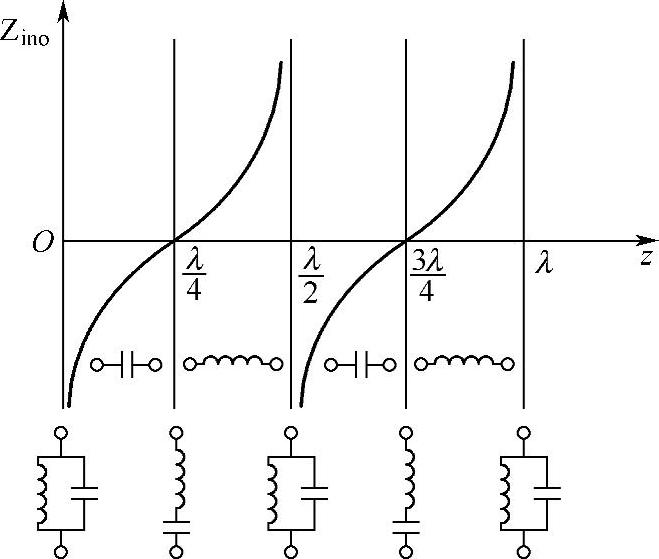
图2-42 终端开路线的输入阻抗
2.反射系数
由传输线方程的解可知,传输线上的电压波和电路波一般由入射波和反射波叠加而成,即由从电源到负载和从负载到电源的波叠加。为了分析传输线的反射特性,在这里引入了反射系数的概念。反射系数定义为:传输线上任意一点z处的反射波电压或电流与入射波电压或电流之比,即

式中,下标i代表入射波,下标r代表反射波。
对均匀无耗传输线来说,任意点反射系数Γ(z)大小相等,沿线只有相位做周期性变化,其周期为λ/2,即反射系数具有λ/2重复性。当Z1=Z0时,Γ1=0,表明没有反射波,传输线上只存在有电源向负载方向传播的行波;当终端开路Z1→∞或终端短路Z1=0或终端接纯电抗负载Z1=jX时,终端反射系数|Γ1|=1,表明入射到终端的波全部被反射回去。而当终端负载为任意数时,则一部分入射波被负载吸收,一部分被反射回去。
设传输线上任意点的反射系数为Γ(z),则该点处的电压及电流表示为
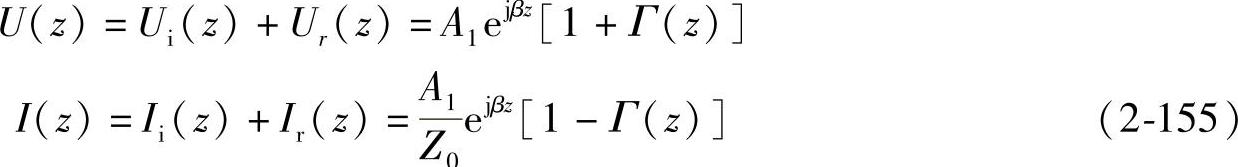
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




