传输线方程及解-车辆电磁兼容基础

1.均匀传输线等效及传输线方程的解

均匀传输线，又称为规则导波系统，指的是截面尺寸、形状、媒质分布、材料及边界条件均不变的导波系统。它可以用两根平行导线来表示，如图2-38a所示。当高频电流通过传输线时，导线将产生热损耗，这表明导线具有分布电阻；由于导线间绝缘不完善而存在漏电流，这表明沿线各处有分布电导；电流通过导线，在周围产生磁场，即导线存在分布电感；两导线间存在电压，其间有电场，则导线间存在分布电容。这四个分布元件可分别用单位长分布电阻R、单位长分布漏电导G、单位长分布电感L和单位长分布电容C来描述，以上参数可通过静态场的分析方法得到，其等效电路如图2-38b所示。

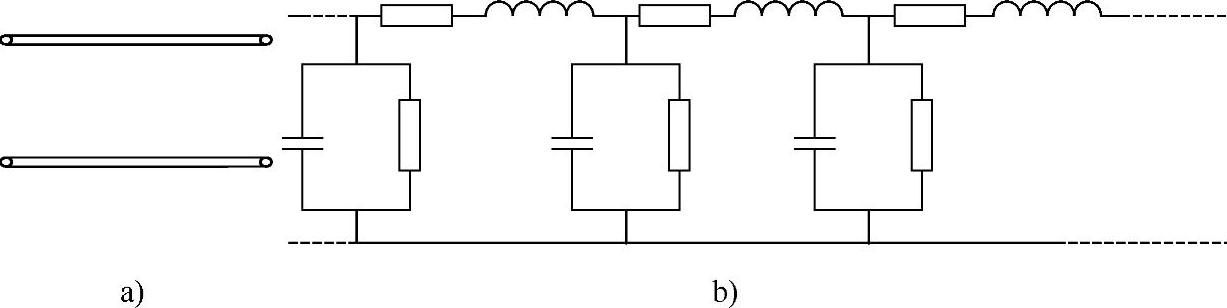
图2-38 均匀传输线及其等效电路

设传输线始端接有内阻为Z_g的信号源，终端接有阻抗为Z_t的负载，并建立坐标，如图2-39a所示。原点在终端负载处，方向由负载指向信号源，其上任意微分小段可等效为电阻RΔz、电感LΔz、电容CΔz和漏电导GΔz组成的网络，如图2-39b所示。设时刻t在离传输线终端z处的电压和电流分别为u（z，t）和i（z，t），而在位置z+Δz处的电压和电流分别为u（z+Δz，t）和i（z+Δz，t），则对很小的Δz应用基尔霍夫定律有

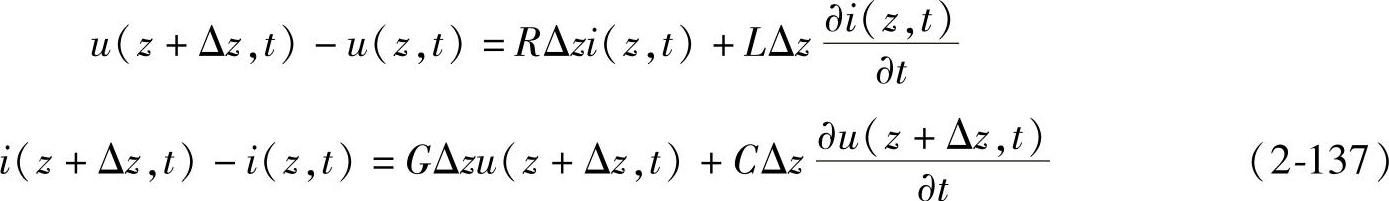
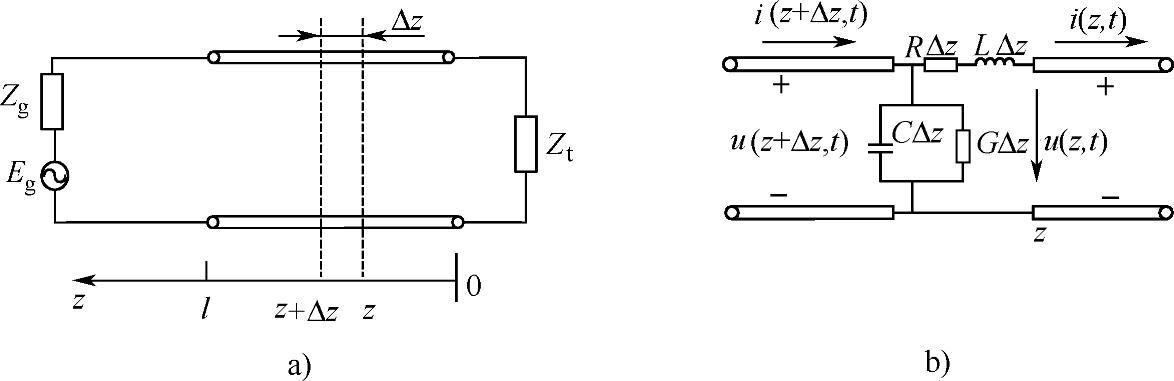
图2-39 传输线系统及微分段的等效电路

a）传输线系统 b）等效电路(www.xing528.com)

对式（2-137）进行整理，并忽略高阶小量。经过推导，可得该二阶微分方程的通解为

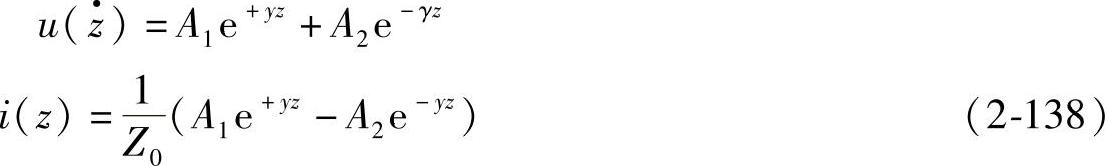
式中，Z=R+jωL（ω是正弦电源的角频率）；γ为传输线的特性阻抗，γ=G+jωC，Z₀=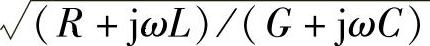；A₁、A₂为积分常数，由传输线的边界条件决定。

2.传输线方程解的分析

在式（2-138）中，令γ=α+jβ，为简单起见，令A₁、A₂、Z₀均为实数并考虑时间因子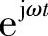，则可得传输线上的电压和电流的瞬时值表达式为

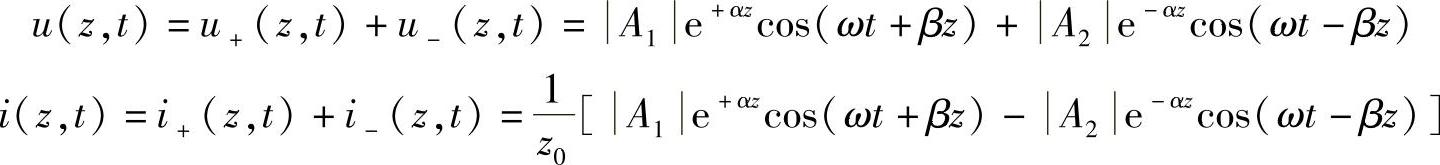
式（2-139）表明，传输线上任意点的电压和电流都由两部分组成，即在任一点z处的电压或电流均由沿-z方向传播的行波（入射波）和沿+z方向传播的行波（反射波）叠加而成。不管是入射波还是反射波，它们都是行波。行波在传播过程中的幅度按e^-αz衰减，因此称α为衰减常数，单位为dB/m；相位随z连续滞后βz，故称β为相位常数，单位为rad/m。