均匀平面波的基本特征

1.一般波动方程

电磁波的存在是麦克斯韦方程组的一个重要结果。1865年，麦克斯韦从他的方程组出发推导出了波动方程，并得到了电磁波速度的一般表示式，由此预言电磁波的存在及电磁波与光波的同一性。1887年，赫兹用实验方法产生和检测了电磁波。

考虑到媒质的无源区域，电容率为ε、磁导率为μ，电导率为σ，这时麦克斯韦方程变为

对式（2-118a）两边取旋度，得

利用矢量恒等关系∇×∇×E=∇（∇·E）-∇²E，又已知∇·E=0，得

∇×∇×E=∇²E

将式（2-118b）代入式（2-119）得

同样可以推导出

式（2-120b）称为一般波动方程，这些方程支配着无源均匀导电媒质中电磁场的行为。在二阶微分方程中，一阶项的存在，表明电磁场在导电媒质中的传播是衰减的（有能量损耗）。因此，导电媒质称为有耗媒质。当媒质完全电介质或无耗媒质即媒质的导电率σ=0时，上述波动方程变为

式（2-121）称为时变亥姆霍兹方程，它表明电磁场在无耗媒质中的传播是不衰减的。对于时谐电磁场，将场量的向量形式代入式（2-121）可得

式中，k²=ω²_με，其中，ω=2πf，是波的角频率，单位为rad/s；f是振荡频率，单位为Hz。式（2-122）称为亥姆霍兹方程，也称为无源、无耗媒质中时谐电磁场的波动方程。

2.无耗媒质中的均匀平面电磁波

如果把电磁波的传播方向称为纵向平面，与传播方向垂直的平面称为横向平面，若场量E和H的分量都在横向平面中，则称这种波为平面电磁波（简称平面波），如图2-29所示。在任意固定时间观察平面波，若它在横向平面中场值的大小和方向不变，则称这种平面波为均匀平面波。例如，沿z轴方向传播的均匀平面波，电场E和磁场H都不是x和y的函数，而只是z的函数，但其方向在xy平面内，即E_z=H_z=0。

电场在时域中的表达式为

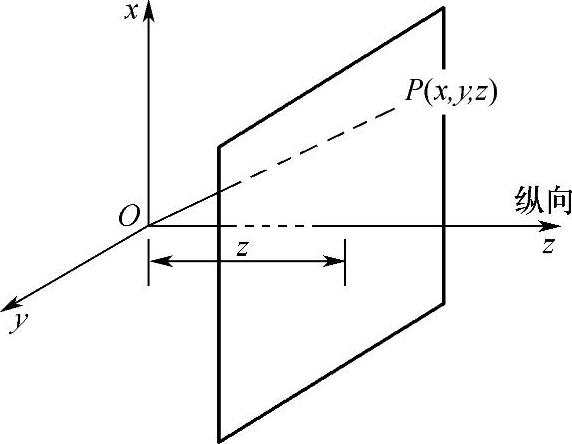
图2-29 平面电磁波

下面对平面波即式（2-123）进行较为仔细的分析，从而建立起电磁波的一些重要概念。

（1）电磁波的相位 式（2-123）中的cos（ωt-kz+φ₀）代表了场的波动状态，称为电磁波的相位。它由三部分构成。其中ωt表示随时间变化部分，-kz表示随空间距离变化部分，φ₀表示场在z=0、t=0时的状态，称为初相位。

（2）行波与相速 平面波在空间某点z=z₀处的电场（E_x）与时间（t）的关系曲线，如图2-30所示。由图可以看出均匀平面波在空间任意观察点处，其场强是以角频率ω随时间按正弦规律变化的。当t增加一个周期，ω=2π/T，场强恢复其初始的大小和相位。

场强也随z变化。图2-31给出的是不同时刻t₁和t₂（t₂＞t₁）电场E_x对距离z的关系曲线。由图2-30及图2-31可见，在任一固定时刻，场强随距离z同样按正弦规律变化，且随着时间的推移函数的各点沿+z方向向前移动，因此称之为行波。

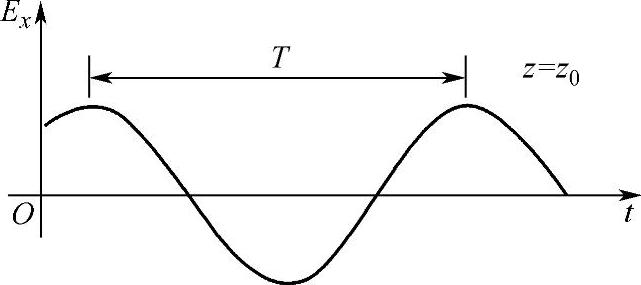
图2-30 电场与时间的关系曲线

图2-31 不同时刻电场与距离z的关系曲线

现在把平面波的相位记为φ=ωt-kz+φ₀，令t=t₀并依次作出φ与z的关系曲线，如图2-32所示。由图可见，在传播方向上行波的相位随距离z的增大而连续滞后。这是行波的一个基本概念。

行波既然是一个行进的波，那么必然可以找到一个物理量来表示其行进速度。定义平面波的等相位面移动的速度称为相速，所谓等相位面即指满足ωt-kz+φ₀=常数的平面。

将上式两边对时间t微分，整理可得行波的相速为

在自由空间中，其介电常数与真空的几乎相同，即ε=，，代入式（2-124）可得其传播相速为v_p=3×10⁸（m/s）=c（真空中的光速）。因此电磁波在自由空间中传播的速度等于光速。相速还可以表示为(www.xing528.com)

式中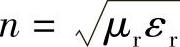，，n为媒质的折射率。显然相速取决于媒质的介电常数和磁导率。如果相速与频率无关，此时的媒质称为非色散媒质，否则称为色散媒质。上述均匀的、线性各向同性的无耗媒质一定是非色散媒质。

图2-32 相位φ与距离z的关系曲线

（3）波长与相位常数 由于平面波在任意给定的时刻（t=t₀），其波形随距离z按正弦波变化，如图2-33所示。因此任意给定时刻相位相差2π的两平面的距离λ称为波长，kλ=2π，即有

另外，由于k=2π/λ表示电磁波单位距离上的相位变化，因此称k为相位常数。

（4）波阻抗与功率密度 由麦克斯韦第二方程得

图2-33 电磁波的波长

将平面波的电场E=a_xE₀e^-jkz代入式（2-127），相应的磁场为

其中，a_z为平面波的传播方向，而

容易得出η的单位是Ω，因此η称为本征阻抗或波阻抗。

无耗媒质中任意点的平均功率流密度为

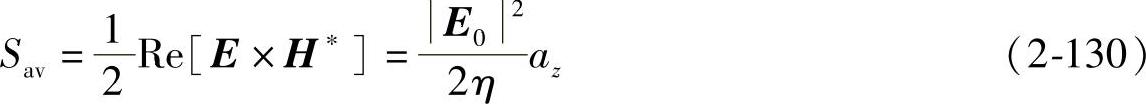
综合以上讨论，可以归纳出在无耗媒质中平面电磁波以光速无衰减地传播；电场与磁场的振幅之比η为常数，故只要求得电场就可求得磁场，即电场和磁场不仅有相同的波形，且在空间同一点具有同样的相位。此外，平面波的电场和磁场均没有纵向分量，只有横向分量，故又称为横电磁波（TEM）波，E、H与S三者互相垂直，且成右手螺旋关系，如图2-34所示。

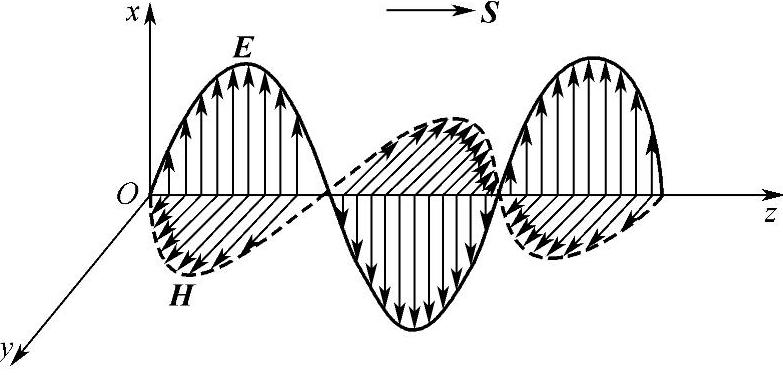
图2-34 无耗媒质中传播的均匀电磁波

3.有耗媒质中的均匀平面电磁波

（1）复介电常数 在导电媒质中，麦克斯韦方程的复数形式可写成

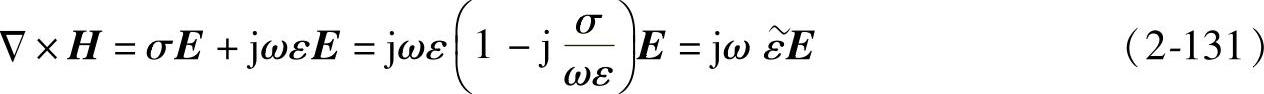
式中，复数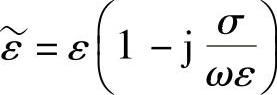，称为导电媒质的复介电常数。其实部代表位移电流的贡献，它不引起功率损耗；而其虚部代表传导电流的贡献，将引起能量的损耗。因此，可以根据传导电流与位移电流的比值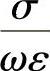的大小对媒质进行分类。若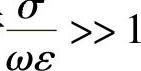，即传导电流占优势，称为导体；若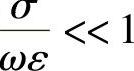，即位移电流占优势，称为绝缘体，亦称电介质；值介于两者之间，称为半导体。由此可见，媒质分类没有绝对的界限。通常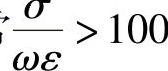时，可认为是导体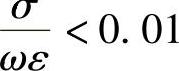；时，可认为是电介质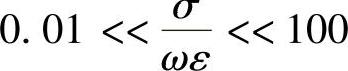；时，则可认为是半导体，或半导电媒质。

因此在时谐电磁场中，对材料性质的划分不仅要考虑材料本身的电导率σ，还要考虑材料的介电常数以及工作频率f。

（2）无限大导电媒质中的均匀平面波 引入复介电常数εv的概念，使导电媒质中的麦克斯韦方程与无耗媒质（电介质）中的麦克斯韦方程形式上完全相同，所不同的是前者为复介电常数。而后者是实介常数ε。因此，只要将无耗煤质场的解答中的ε用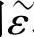取代即可得导电煤质中场的表达式。在无耗煤质的解中，有两处出现ε，一个是相位常数k，另一个是波阻抗η。

将无耗煤质的相位常数k及波阻抗η中的ε均以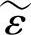来取代，即得导电煤质中的复相位常数和复波阻抗，即

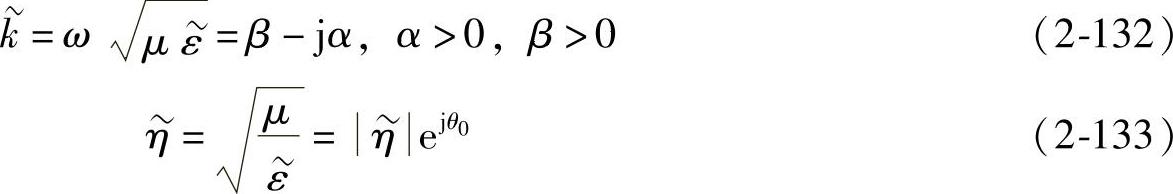
将电介质中电磁场表达式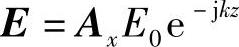及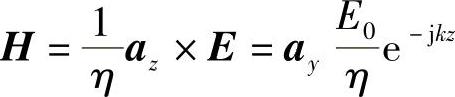中的k和η分别取代以k和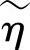，得

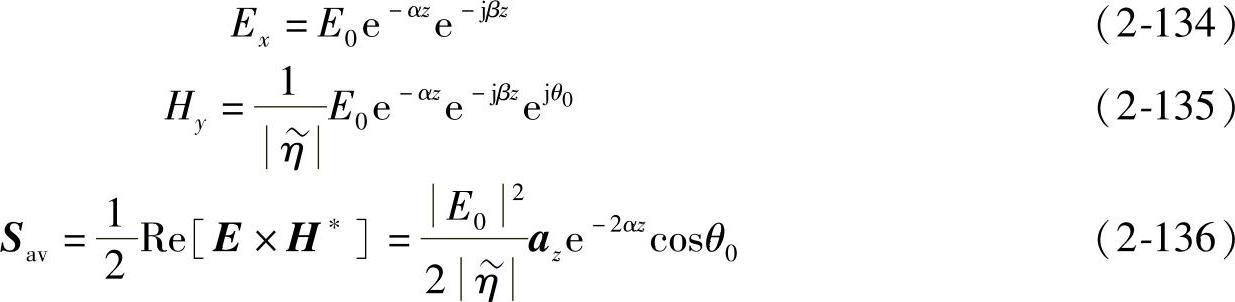
图2-35 有耗煤质中的均匀平面波

由以上分析可见，导电媒质中的均匀平面波仍是横电磁波（TEM波），这个波是一个衰减的行波，简称衰减波。衰减是传导电流引起的，电场和磁场的振幅随距离按指数规律e^αz衰减，衰减速度取决于α，称为衰减常数，单位为Np/m（奈贝/米），而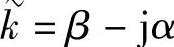中的另一个参数β表示传播过程中相位的变化，称为相位常数，所以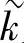又称为传播常数。还需注意，电场和磁场相位是不相同的，彼此间存在一个固定的相位差θ₀。有耗煤质中的均匀平面波如图2-53所示。