车辆电磁兼容基础：电磁场基本定律及其修正

1.静电场的基本定律

由静止电荷产生的电场不随时间而变化，称为静电场。电通密度D可以用电场强度E定义为

D=ε₀E （2-79）

式中，ε₀为真空的介电常数（ε₀=8.85422×10^-12F/m）。D的单位为库仑每平方米（C/m²）。通过电通密度D来定义电通量Φ为

式中，dS为S面上的面微分元，如果D与dS方向相同，则通过S面的电通量最大。

高斯定律：通过任一闭合面S的净穿出电通量，等于该曲面所包围的静电荷Q，即

如果式（2-81）中的Q用S中电荷密度的积分表示，并用散度定理将左边的面积转化成体积积分，则有

式中，ρ_V是媒质中的自由体电荷密度。在导体中ρ_V为0；在电介质中，ρ_V纯属自由电荷，因为极化电荷的效应已包含在相对电容率ε_r中。因为S（及其所包围的体积V）是任意的，所以式中的被积函数应相等，即

式（2-83）是高斯定律的微分形式，其含义为：空间任意存在正电荷密度的点都在发出电通量线。如果电荷密度为负，则电通量线指向电荷所在点。式（2-83）表明电通密度常常是区域内自由电荷多少的量度。

这些论点同样适用于时变电磁场，唯一不同的是，在时变场中D与ρ_V两者都是时变场量。式（2-83）是麦克斯韦四个方程式之一，它也可以用积分形式表示为

2.静磁场的基本定律

（1）磁高斯定律 磁感应强度B通过任一闭合面S的通量恒等于零，即

由散度定理，得其微分形式为

∇·B=0 （2-86）

与静电场不同，B的散度恒为零。所以B是无散场或叫管形场，B线必定是闭合曲线。虽然上面讨论的磁场是恒定电流产生的，但式（2-85）与（2-86）适用于电流以任何形式随时间变化的情况，即在时变电磁场中也是适用的。式（2-85）和式（2-86）是麦克斯韦四个方程式中的两个。

（2）安培环路定律 自由空间的磁场强度H为

式中，真空磁导率μ₀=4π×10^-7H/m。

由式（2-87）可知，磁场强度与磁导率无关，B与H的关系类似于D与E的关系，显然B与H是同方向的。

安培环路定律又叫安培定律，它阐明沿一闭合路径的磁场强度的线积分等于与此路径交链的总电流，即

式（2-88）中I是闭合路径交链的总电流。其中与该路径环形方向成右旋关系的为正，反之为负。在静磁学中，只要电流或电流分布是高度对称的，就可用安培定律简便地求出磁场。

电流又可以用体电流密度表示为

因此

这是安培定律的积分形式。对式（2-90）用斯托克斯定理将线积分改用面积分，得

因此S可以是闭合路径l所包围的任意开表面，式（2-91）又可以写成

∇×H=J_V （2-92）

这是安培环路定律的微分形式。它表明电流是B场的旋涡源，这与静电场旋度恒为零不同。

对式（2-92）两边同时取散度，并注意∇·（∇×H）=0，则有

∇·J_V=0 （2-93）

但对于时变场，∇·J_V不一定为零。事实上，由后述章节连续性方程可知

(www.xing528.com)

式中，ρ_V为体电荷密度。麦克斯韦把恒定磁场中的安培定律用于时变场时出现了矛盾，为此，提出了位移电流的假说，对安培定律做了修正。位移电流的假说就是变化的电场产生磁场的结果。

设一个电容器与时变电源相连，外加电源电压随时间上升或下降，表征由电源送至每一极板上的电荷量q在变化。电荷的变化形成随时间变化的电流，该时变电流i（t）必然在此区域内建立时变磁场。选择一个闭合路径c，包围电容器外的开曲面S，如图2-26所示。

由安培定律得

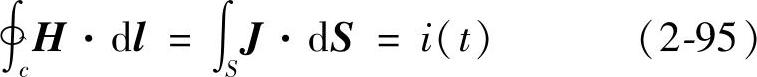
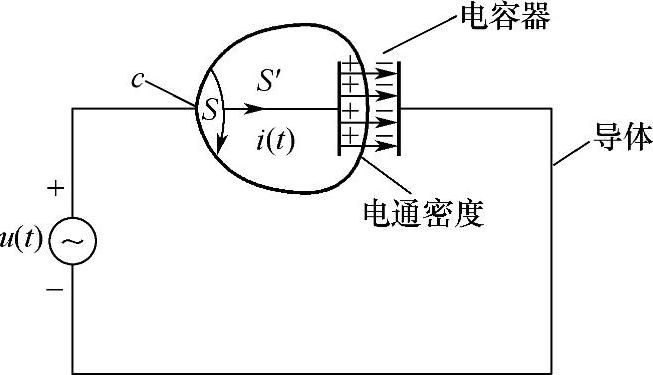
图2-26 电容器的位移电流

但若考虑同一路径C所包围的包含电容器极板的另一个开曲面S′，由于电容器内传导电流等于零，故

式（2-95）与（2-96）显然相互矛盾，因此麦克斯韦断言，电容器中必然有电流存在。由于这种电流并非由传导产生，他认为在电容器的两极板间存在另一种电流，其量值与传导电流相等，因为对于S和S′构成的闭合面，应用电流连续性方程，有

再对式（2-97）应用高斯定理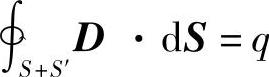，则有

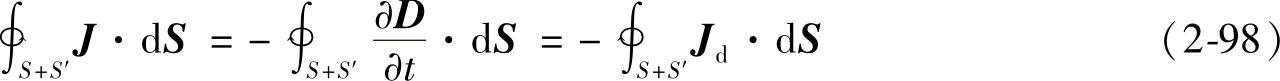
即

麦克斯韦称式（2-99）为位移电流密度，单位为A/m²。

一般来说，空间同时存在传导电流和位移电流，所以，安培定律的修正形式为

式（2-100）称为全电流定律，它表明时变场中的磁场是由传导电流和位移电流共同产生的，位移电流产生磁效应代表了变化的电场能够产生磁场。其微分形式为

对安培定律的修正是麦克斯韦最重大的贡献之一。正是由这一项的存在，使麦克斯韦能够预言电磁场将在空间以波的形式传播。1880年，赫兹用实验证明了电磁波的存在，并证实了波的性质正如麦克斯韦所预言的。

3.时变电磁场的基本定律

在某个区域中，如果存在时变的电（磁）场，则同时存在时变的磁（电）场。

1831年，法拉第发现电磁感应现象，这是人们第一次对随时间变化的电磁场进行研究。法拉第定理表示随时间变化的磁场会产生电场。

如图2-27所示，穿过闭合导线l所包围的面积S的磁通量Φ随时间变化率的负数，即为感应电动势u_emf，且

u_emf的大小等于穿过闭合导线l所包围面积S的磁通量Φ随时间变化率的负数，即

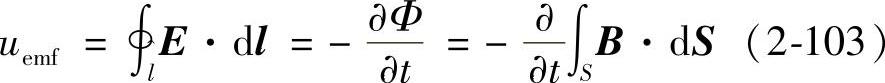
因为微分对时间坐标进行，积分对空间坐标进行，两者次序可调换，这样就得到

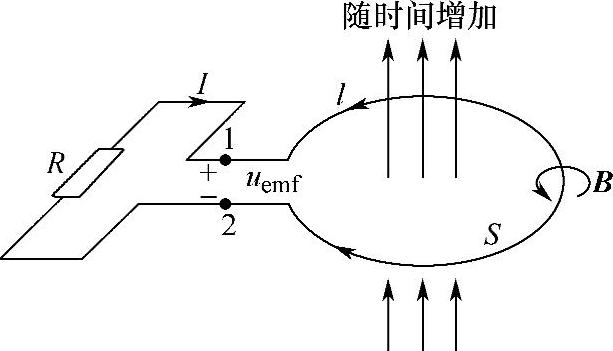
图2-27 穿过闭合导线l的磁通量随时间变化会产生一个感应电动势

这就是积分形式的法拉第定理。图2-28所示为法拉第定理的原理实验装置。矩形导电线圈与一个电流计相连，如有电流通过线圈，电流计指针将偏转。螺线管与电池连接，当螺线管与电池接通，流过螺线管的电流就会产生磁场，部分磁力线穿过矩形导电线圈包围的面积。不管采用什么方法，如螺线管与电池的接通或断开，通电螺线管靠近或远离矩形导电线圈等，只要使螺线管产生的磁力线穿过线圈包围面积的磁通量Φ随时间变化，电流计指针就会偏转，表示矩形线圈上有电流通过。此电流由感应电动势u_emf驱动，而指针偏转的大小反映了电动势的大小。指针偏转的方向，也就是电流的方向，取决于感应电动势的符号。实验得出的规律是，感应电动势v_emf的大小与穿过线圈的磁通量随时间的变化率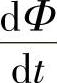成正比，而感应电动势驱动的电流方向，使得该电流激发的磁场抵抗螺线管产生的磁场随时间的变化，式（2-103）右边的符号就说明了这一点。

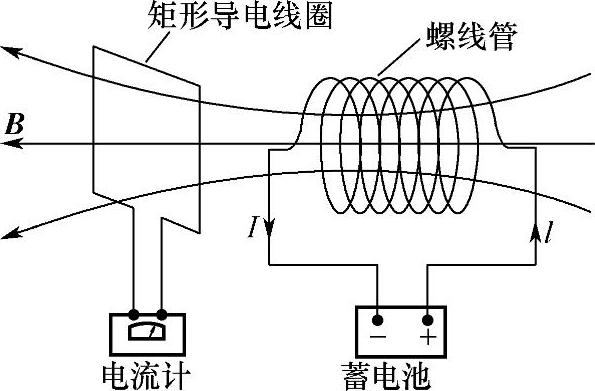
图2-28 法拉第定理的原理实验装置

对式（2-104）用斯托克斯定理，可将沿闭合路径l的线积分变换成由l包围的面积S的面积分，即

由于方程式两边的被积函数相等时才能成立，即

式（2-106）是著名的麦克斯韦四个方程式之一，它是麦克斯韦方程（法拉第定律）的点函数形式或微分形式。此式可用以求出当磁场是时间函数时空间某定点的电场强度。对于静态场，它简化为∇×E=0。