骚扰信号的频域描述及频谱分析

骚扰信号的频域描述即骚扰信号的频谱分析。了解骚扰的频谱就可以确定骚扰会在哪些频段上对其他设备产生干扰。如果骚扰的频谱范围与设备的通频带没有重叠，一般不会产生干扰（除非骚扰强度特别高），反之就有可能产生危害。有关电磁兼容的国际国内标准都是在频域上确定骚扰限值的。例如，在国标GB 14023—2011《车辆、船和由内燃机驱动的装置无线电骚扰特性限值和测量方法》中规定了车辆、船和配有内燃机的装置等设备向空间辐射的骚扰场强在10m处限值，用于对居住环境中使用的广播接收机在30～1000MHz频率范围内提供保护。在30～230MHz频段内骚扰场强应小于30dB，在230～1000MHz频段内骚扰场强应小于37dB。在对骚扰采取抑制措施时也必须考虑骚扰信号的频率范围，不同的频段采用的方法可能不同。常用的骚扰抑制器件如滤波器、磁环、屏蔽材料等都是在一定频率范围内才能起作用，所以电磁骚扰频谱的研究在电磁兼容分析中起着重要的作用。

1.频谱

利用傅里叶级数（对于周期性骚扰信号）或傅里叶积分（对于非周期骚扰信号），可将任何骚扰信号分解成不同频率简谐信号的叠加。这些简谐信号的幅值随频率变化的函数（C_n或F（ω）），称为骚扰信号的频谱。

2.周期性骚扰信号的频谱

大多数功能性骚扰源产生的都是周期性骚扰信号。设f（t）是一个周期性骚扰信号，可以用傅里叶级数展开为

ω₀是基波，nω₀表示各次谐波频率分量的幅度。周期性骚扰信号也可以展开为实数形式

[例2-1] 求一个周期方波信号f（t）的频谱，如图2-1所示，T是方波信号的周期。

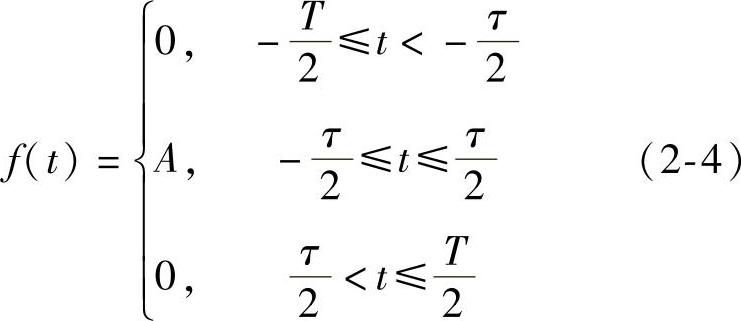
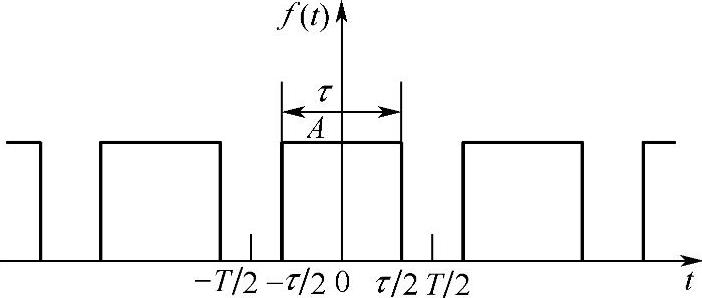
图2-1 周期性方波信号

解：把式（2-4）代入式（2-2）可得：

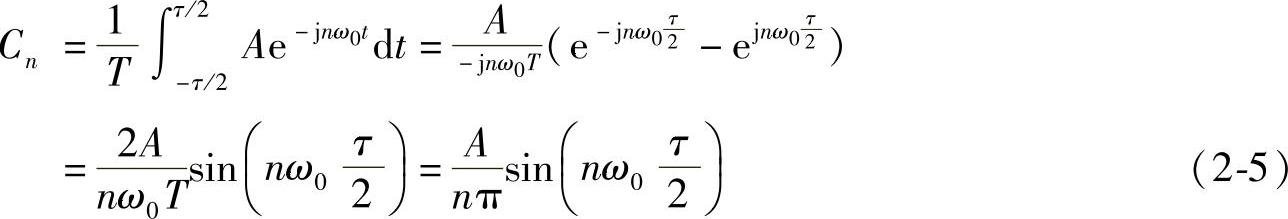
式中，ω₀=2π/T，所以周期性方波信号f（t）可以展开为

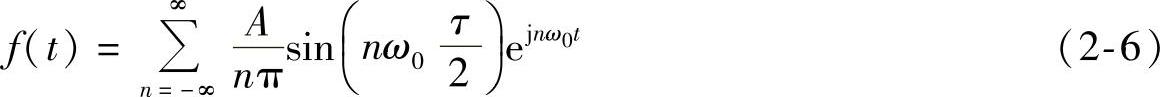
利用式（2-5）可以画出周期性方波信号f（t）的频谱曲线，设τ=T/4，则可以算出基波和各次谐波的幅度，见表2-1。

表2-1 基波和各次谐波的幅度

利用表2-1中的数据可以画出周期性方波信号f（t）的频谱曲线，如图2-2所示。

由图2-2可以看出，周期性骚扰信号频谱的特点如下：

（1）离散性 周期信号的频谱由不连续的谱线组成，谱线间隔为ω₀，每条谱线代表一个正弦分量。

（2）谐波性 周期信号频谱的每一条谱线，只能出现在基频的整数倍的频率上。

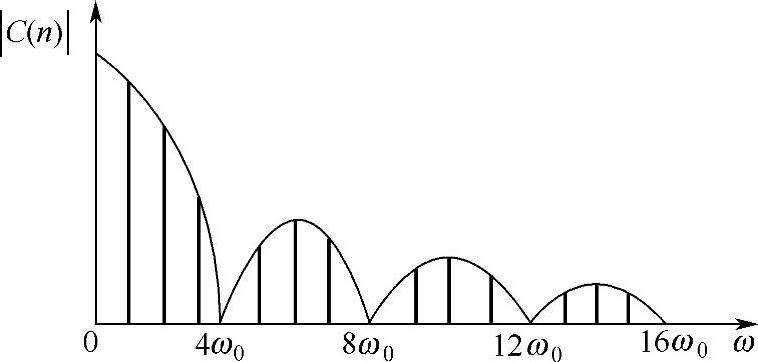
图2-2 周期性方波信号的频谱

（3）收敛性 各次谐波的幅值随频率的增加而减小，频谱是收敛的。

完整的周期性方波信号的频谱如图2-3所示。

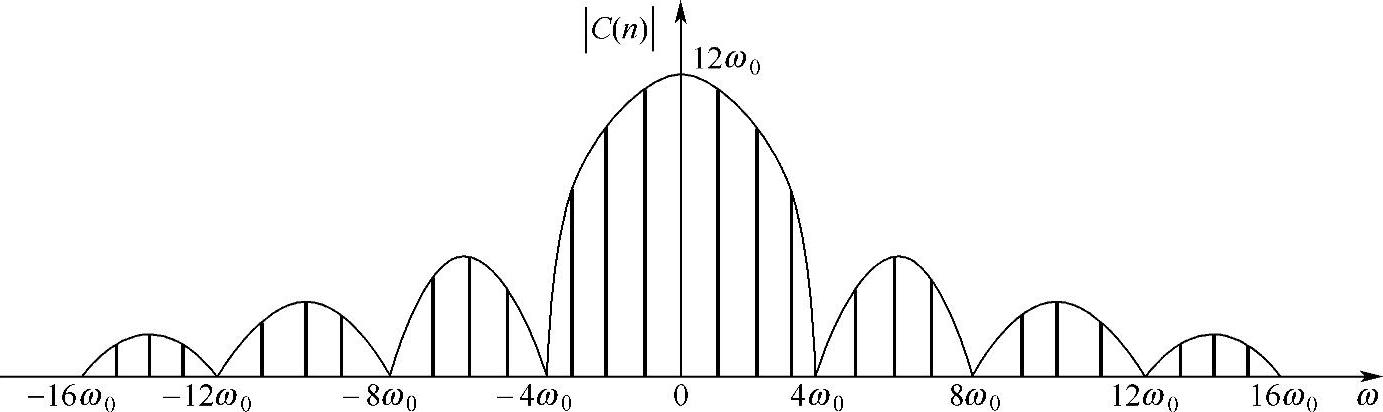
图2-3 完整的周期性方波信号的频谱

除了基波和各次谐波信号以外，骚扰源还可能产生一些寄生信号，频率低于或高于基波频率，但不是基本频率的整数倍，称为非谐波骚扰。非谐波骚扰信号的电平一般低于谐波骚扰信号，在一些情况也可能成为严重的干扰。

3.非周期性骚扰信号的频谱

大多数非功能性骚扰源产生的都是非周期性骚扰信号。设f（t）是一个非周期性骚扰信号，可以利用傅里叶积分展开为

式中，F（ω）是非周期性骚扰信号f（t）的频谱函数，可以写为

[例2-2] 一个尖脉冲

(www.xing528.com)

且

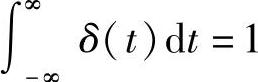，求频谱函数F（ω）。

解：把式（2-9）代入式（2-8）可得

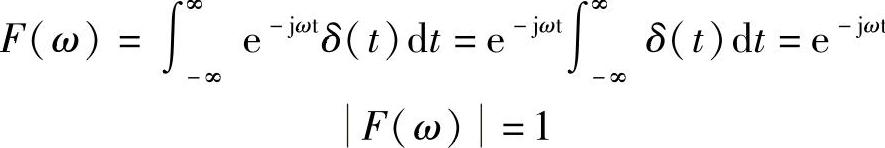
因此，其频谱函数|F（ω）|=1。

一个周期性信号，当周期T→∞时就成为非周期性信号。例如，如图2-4所示，一个周期性方波信号f（t），随着周期T增大，谱线间隔减小，谱线变密；当T→∞时，谱线间隔→0，谱线成为连续的，此时就称为一个孤立的矩形脉冲信号。所以非周期性骚扰信号的频谱是连续的，也是收敛的。

一些常见的脉冲信号的频谱见附录。

由这些脉冲的频谱可知，能量主要集中在频率较低的频段，随着频率的升高，频谱幅度越来越小，最后可以忽略不计。以下以矩形脉冲为例说明频谱幅度与频率的关系。

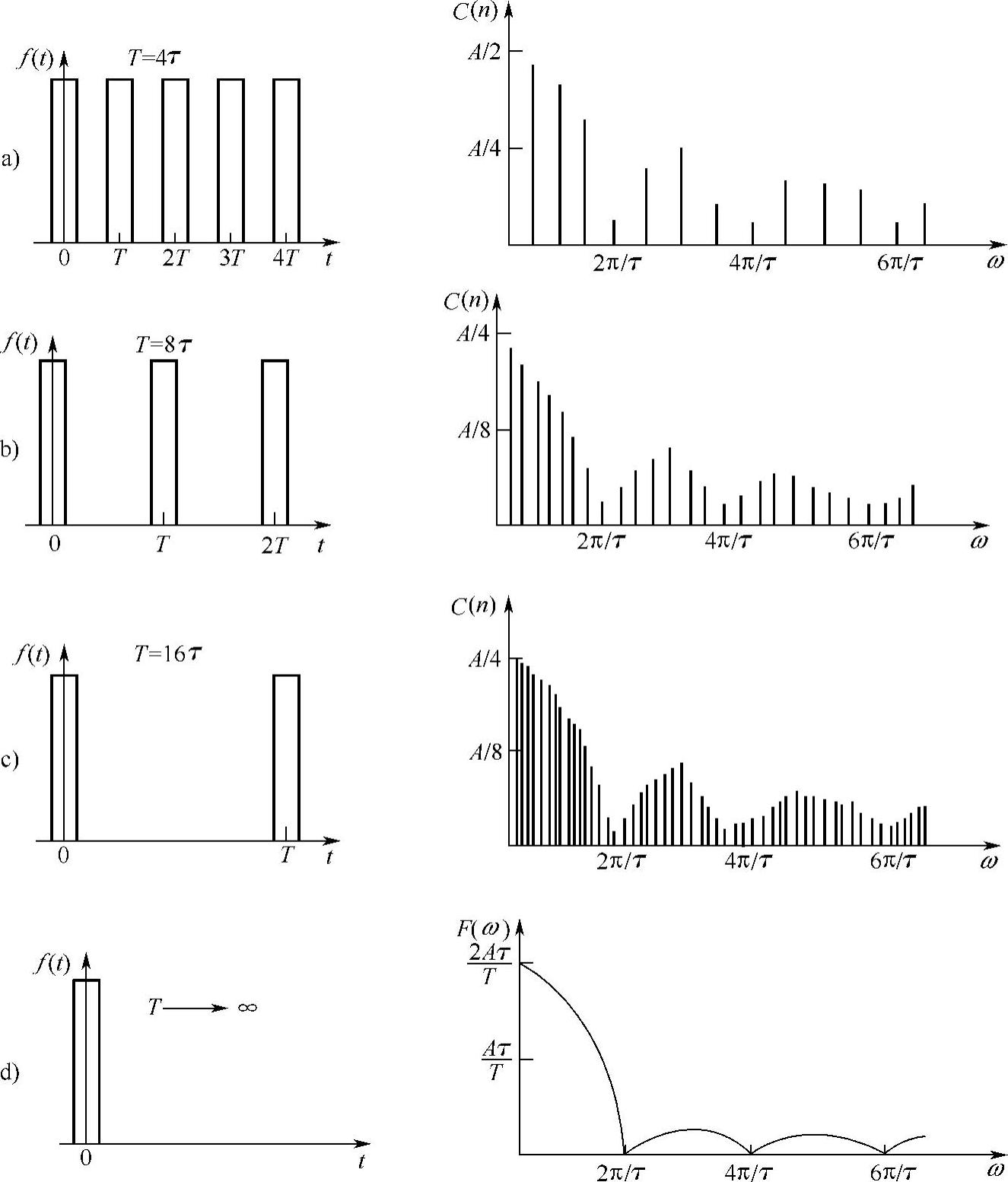
图2-4 一个周期性方波信号，随着周期T增大，谱线变密

矩形脉冲的频谱由主瓣和无数个副瓣组成，每个副瓣虽然也有最大值，但总的趋势是随频率的升高而降低。图2-5所示为一个幅度A=1V、宽度γ=1μs的矩形脉冲的频谱。为了分析方便，频率轴使用对数坐标，单位为MHz，频谱函数取绝对值，即把负频率部分和正频率部分合并，取频率f为0→∞，幅度轴也使用对数坐标，单位是dB（0dB=1μV/MHz），于是频谱函数可改成

由式（2-10）可知这是个sinx/x函数，由于当|x|＜1时sinx/x≈1，因此可得

对于幅度为1V、宽度为1μs的矩形脉冲可得

e=20lg（2Aτ）=126dB（μV/MHz）

如果把频谱中各副瓣的最大值用一条假想的切线连接起来，则由式（2-10）可求出该切线的斜率。已知各副瓣的最大值为

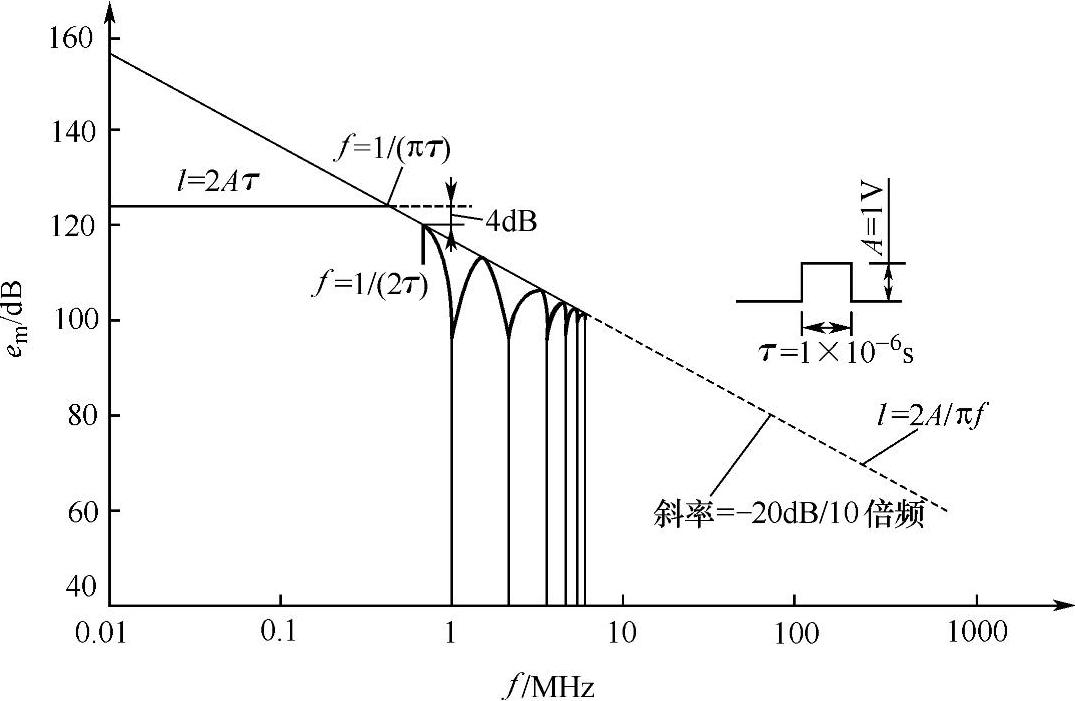
图2-5 矩形脉冲（1V，1μs）的频谱

注：取lμV/MHz为OdB

由式（2-13）可知副瓣最大值的切线率为-20dB/10倍频。

以上分析说明，矩形脉冲的频谱在低频段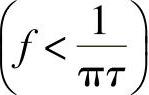时幅度基本不变，e=2Aτ，而在高频段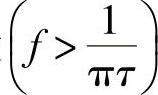时总的趋势是幅度以每10倍频20dB的速率下降。利用同样的方法可以画出其他脉冲波形的频谱（包括切线随频率变化）的比较图。图2-6列出了8种脉冲频谱的比较图，所有脉冲幅度均为1V，宽度为1μs。

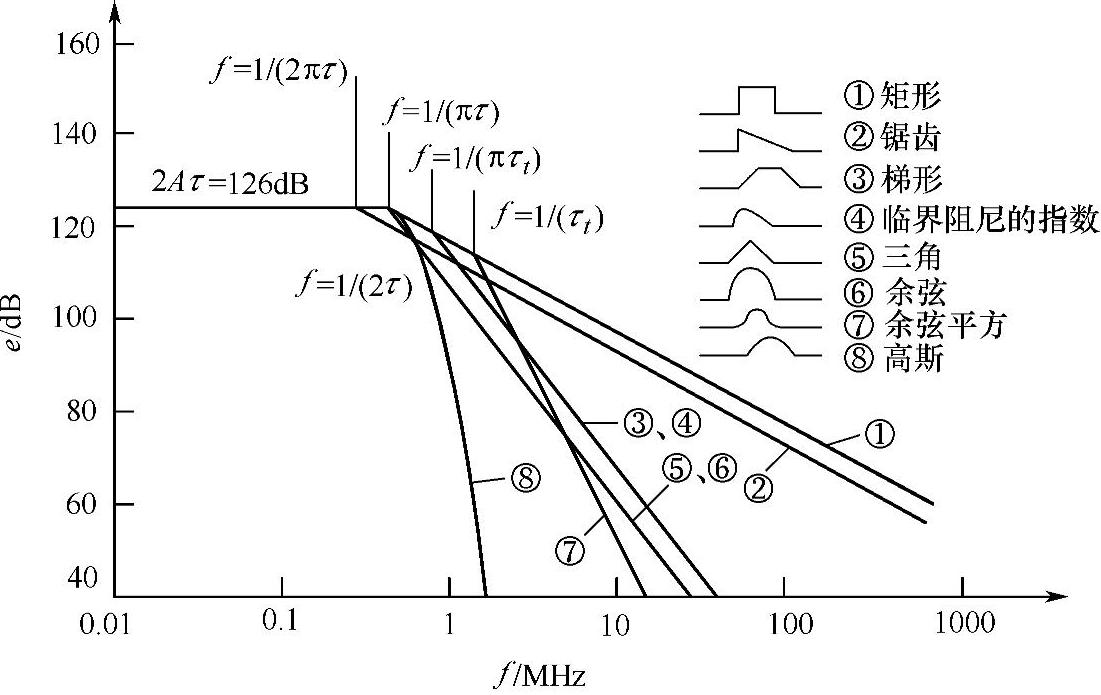
图2-68 种脉冲频谱的比较

注：取lμV/MHz为OdB

由图2-6可知，在低频段各种脉冲的频谱幅度是相同的，但在高频段幅度的衰减情况就大不相同。对于矩形和锯齿形脉冲，其幅度随频率的下降最慢为20dB/10倍频；对于梯形、临界阻尼指数形、三角形、余弦形脉冲则以40dB/10倍频速度下降；对于余弦平方形脉冲下降速率为60dB/10倍频；高斯形脉冲下降最快速率为80dB/10倍频。比较8种脉冲波形的频谱可以得出以下重要结论：

1）脉冲波形具有相当宽的频率带宽。

2）脉冲波形的频谱幅度在低频段较高，在高频段随频率增加而降低，降低的速率与脉冲边沿的陡度有关。脉冲越陡峭即上升时间越短，则频谱幅度下降越慢；反之，脉冲越圆滑下降速率越快。换而言之，陡峭的脉冲比圆滑脉冲含有更高的频率成分，有效频率带宽更宽。

从电磁兼容的角度看，脉冲的频率带宽太宽是我们不希望的，因为高频成分比低频成分更容易通过辐射或耦合途径传输，从而对其他设备产生干扰。例如，在数字电路中常用梯形脉冲来代替矩形脉冲作为数字信号，因为矩形脉冲的前沿十分陡峭，含有丰富的高频成分，容易在电路内部产生相互干扰，也容易干扰其他电路如模拟电路。而梯形脉冲具有一定的上升时间和下降时间，在保证逻辑功能正常进行的情况下还应尽可能地增加其上升、下降时间。上升时间为τ_t、宽度为τ的梯形脉冲频谱峰值包络图如图2-7所示。图中有两个转折点，一个是1/πτ，另一个是1/πτ_t。频谱幅度在低频段是常数，经第一转折点1/πτ以后以20dB/10倍频下降，经第二转折点1/πτ_t以后以40dB/10倍频速率下降。通常在第二转折点的频谱幅度比第一转折点低10dB左右，所以一般把

作为梯形脉冲频率带宽的高端，高于该频率的谐波可以认为能量很小，可以忽略不计，即梯形脉冲的频率带宽为0～πτ_t。例如，脉冲上升时间πτ_t为1ns，则根据式（2-14）可知，应考虑的最高频率为318MHz。有时候只知道数字电路的时钟频率或脉冲的重复频率f_PR，并不确切地知道其脉冲上升时间，则一般要求考虑的最高频率应为

式（2-14）和式（2-15）提供的脉冲应考虑的最高频率估算方法在电磁兼容分析中是很重要的，其他形状的脉冲也可用此法估算。

图2-7 梯形脉冲的频谱