直线上的点的投影成果与比例（建筑制图）

12.3.1　直线上点的投影

在空间上，直线与点的相对位置有两种情况，即点在直线上和点不在直线上。

若点在直线上，则该点的各个投影一定在直线的同面投影上，且符合点的投影规律，如图3.36（a）所示。反之，点的各投影都在直线的同面投影上，且符合点的投影规律，则该点一定在直线上。在图3.36（b）中，由于c 在ab 上，c′在a′b′上，且cc′⊥ox，所以C 点在AB 上。

12.3.2　直线上取点

图3.36（a）中，C 点把AB 分成AC 和CB 两段，设这两段长度之比为m∶n，则有AC∶CB=ac∶cb= a′c′ ∶c′b′=m∶n。即点将直线段分成定比，则该点的各个投影必将该线段的同面投影分成相同的比例。这个关系称为定比关系。

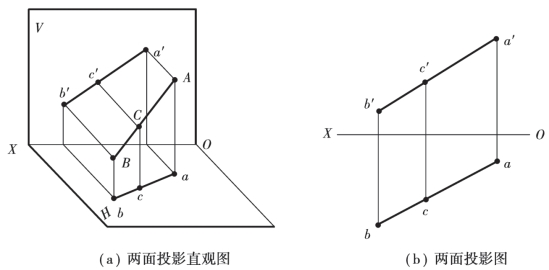
图3.36　直线上的点

例3.3 已知C 点把线段AB 按2∶1 分成两段，求C 点的两个投影，如图3.37 所示。(www.xing528.com)

解 过a 作辅助线aB0，并在该线段上截取3 等份；连接bB0；过二等分点C0 作bB0 的平行线，其与ab 的交点即为C 点的水平投影c；最后利用点的投影性质求出c′。

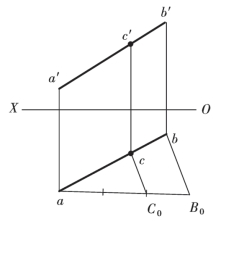
图3.37　一般位置直线上取点

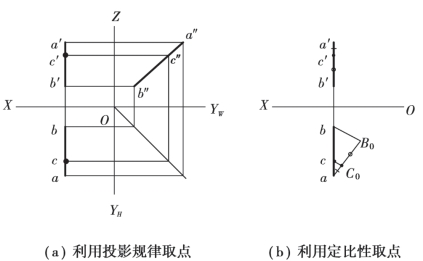
图3.38　侧平线上取点

例3.4 已知在侧平线AB 上一点C 的正面投影c′，求其水平投影c。

方法1：因为C 点在AB 上，它的各个投影均应在直线的同面投影上，所以可先作出直线的侧面投影a″b″，由c′定出c″，再求出C 点的水平投影c ，如图3.38（a）所示。

方法2：过a 作辅助线aB0，并在该线段上截取aC0= a′c′，C0 B0= c′b′；连接bB0；过C0作bB0 的平行线，其与ab 的交点即为C 点的水平投影c，如图3.38（b）所示。