手工制图工具和仪器的应用

建筑物的构件轮廓都是由直线圆弧曲线等几何图形所组成。因此，掌握基本几何图形正确的作图方法，对提高绘图的速度和精确度是很重要的。

6.2.1　平行线垂直线及等分线

①过已知点作已知直线的平行线，如图2.6 所示。

微课 线及多边形的绘制

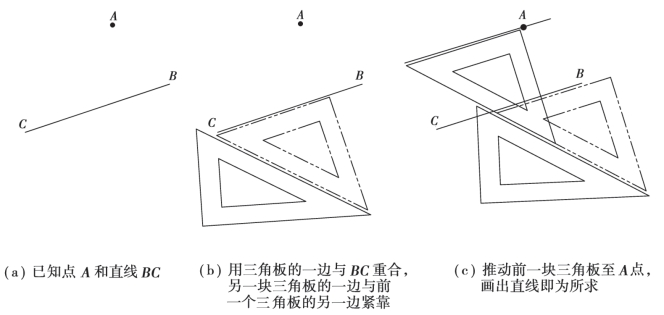
图2.6　过已知点作已知直线的平行线

②过已知点作已知直线的垂直线，如图2.7 所示。

③分已知线段为任意等分，如图2.8 所示。

④分两平行线之间的距离为已知等分，如图2.9 所示。

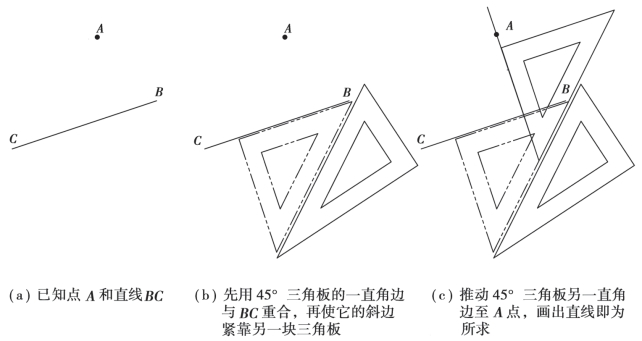
图2.7　过已知点作已知直线的垂线

图2.8　分已知线段为五等分

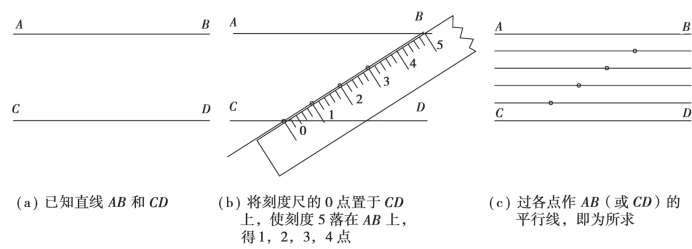
图2.9　分两平行线之间的距离为五等分

6.2.2　正多边形(www.xing528.com)

圆内接正多边形，可采用三角板与丁字尺配合使用求出。

①圆内接正五边形，如图2.10 所示。

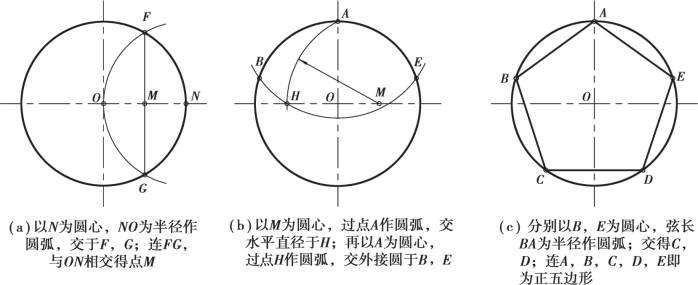
图2.10　圆内接正五边形作法

②圆内接正六边形，如图2.11 所示。

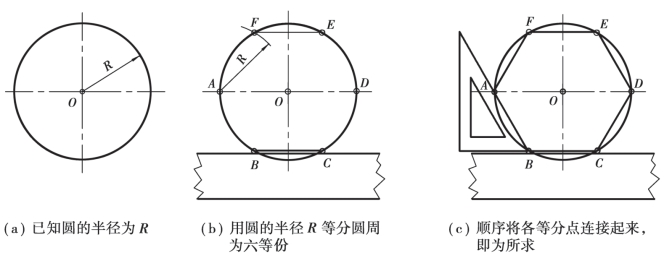
图2.11　圆内接正六边形作法

③圆内接任意正多边形，如图2.12 所示。

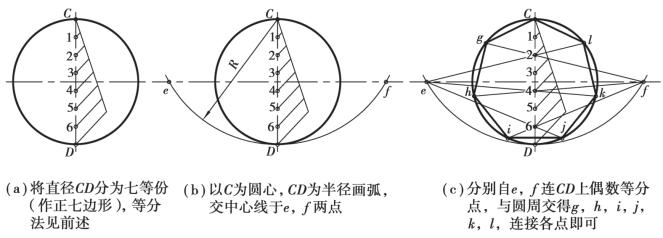
图2.12　圆内接任意正多边形作法

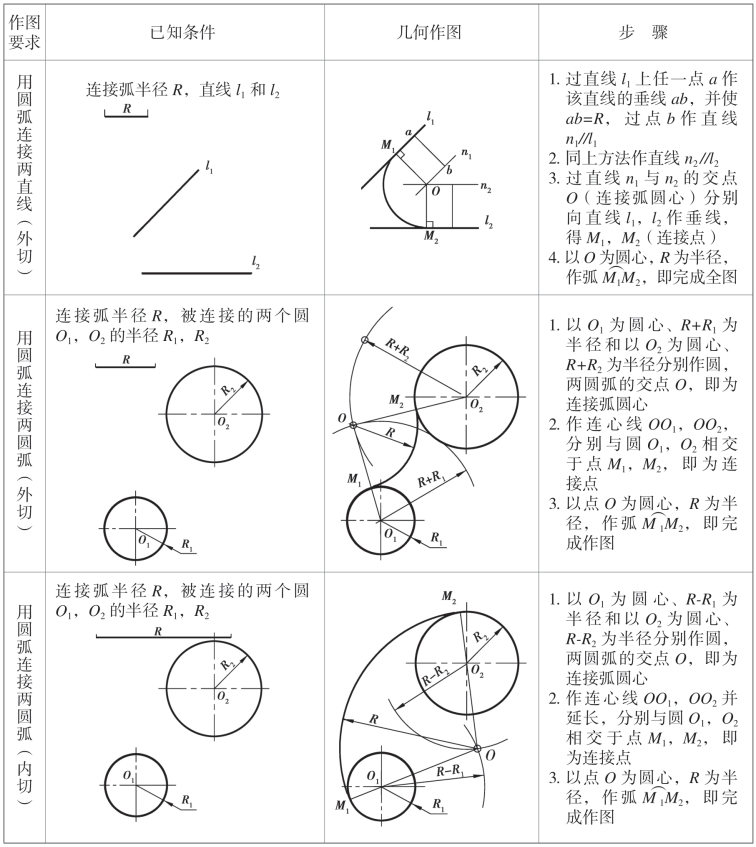
6.2.3　圆弧连接

在设计平面图形时，有时需要从一条直线（或圆弧）经圆弧光滑地过渡到另一条直线（或圆弧），我们称这种作图为圆弧连接。在中间起连接作用的圆弧称为连接弧。连接弧与直线（或圆弧）的光滑过渡实质是直线（或圆弧）与圆弧相切，切点就是连接点。

为实现圆弧连接，必须根据已知条件和连接弧的半径R，求出连接弧的圆心和连接点（切点），才可保证光滑连接。尺规作图方法和步骤见表2.1。

微课 弧线的绘制

表2.1　圆弧连接