模糊综合评价的原理与方法

模糊综合评价法是一种基于模糊数学的综合评标方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰、系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决^[20]。而实际上，建筑遗产保护利用作为一个包罗万象的复杂巨系统，各种因素相互交错而很难绝对分离，而且具有多层次性，在建筑遗产综合价值评价中，价值评价作为对评价主体需要满足程度的量化衡量，无论采取何种技术手段，其结果都是难以精确计算的，我们能做的只是尽最大可能接近其综合价值的实际大小，而模糊综合评价对这样的问题来说可谓非常适合。因此，通过引入模糊数学中的隶属度理论与模糊评价方法，进行综合价值的模糊评价，有助于在复杂的层次关系中建立系统性，并将定性评价转化为定量评价，增加评价的科学性。

1）确定评价指标的隶属度

在确定评价指标隶属函数及隶属度值时，将近现代建筑遗产价值评价的每个指标水平根据九级记分制，标准赋值介于1～9之间，即分别为很差（1）、较差（3）、一般（5）、良好（7）、优秀（9）。第i评价因子的隶属度，其线性函数表达式可定义如下^[21]：

“很差级”隶属函数为：

“较差级”隶属函数为：

“一般级”隶属函数为：

“良好级”隶属函数为：

“优秀级”隶属函数为：

(www.xing528.com)

将指标量化后得到的数值N分别带入隶属函数，可得到指标对5个等级的隶属值。隶属函数图如图3－11所示。

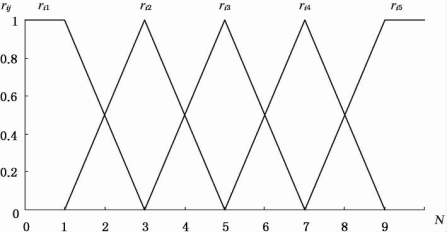
图3－11　隶属函数图

图片来源：周红波，姚浩.城市既有工业建筑可持续改造利用模糊综合评价［J］.建筑管理现代化，2008（6）：28－31

2）模糊评价的步骤^[22]

①将评价因子集按因子的属性分成8个子集，记作u1，u2，…，u8；满足：

设子集Ui＝｛ui1，ui2，…，uin｝，按一级模型分别进行综合评判，假定评判集V＝｛v1，v2，…，v5｝，Ui中的权值分配为Wi＝｛wi1，wi2，…，win｝，要求的单因素的评价矩阵为Ri，于是第一级综合评判为：Bi＝Wi×Ri＝［bi1，bi2，…，bin］

②Ui作为一个元素看待，用Bi作为它的单因素评判，这样

是｛U1，U2，…，U8｝的单因素评价矩阵，每个Ui作为U中的一部分，反映U的某种属性，可按它们的重要性给出权值分配：W＝（w1，w2，…，w8），则得第二级综合评价：

根据最大隶属度原则可确定建筑遗产综合价值指标的等级。