近现代建筑遗产保护与再利用评价方法汇总

综合评价在很多学科领域得到了广泛应用，在实践层面各种类型和特征的综合评价方法也不断推陈出新。表1－1中总结了国内外各学科领域的一些常见的综合评价方法，并从各方法的基本原理、特征、优缺点等方面进行了总结，针对性地指出这些综合评价方法在建筑学科内的应用范围。

表1－1　常用的综合评价方法比较与汇总

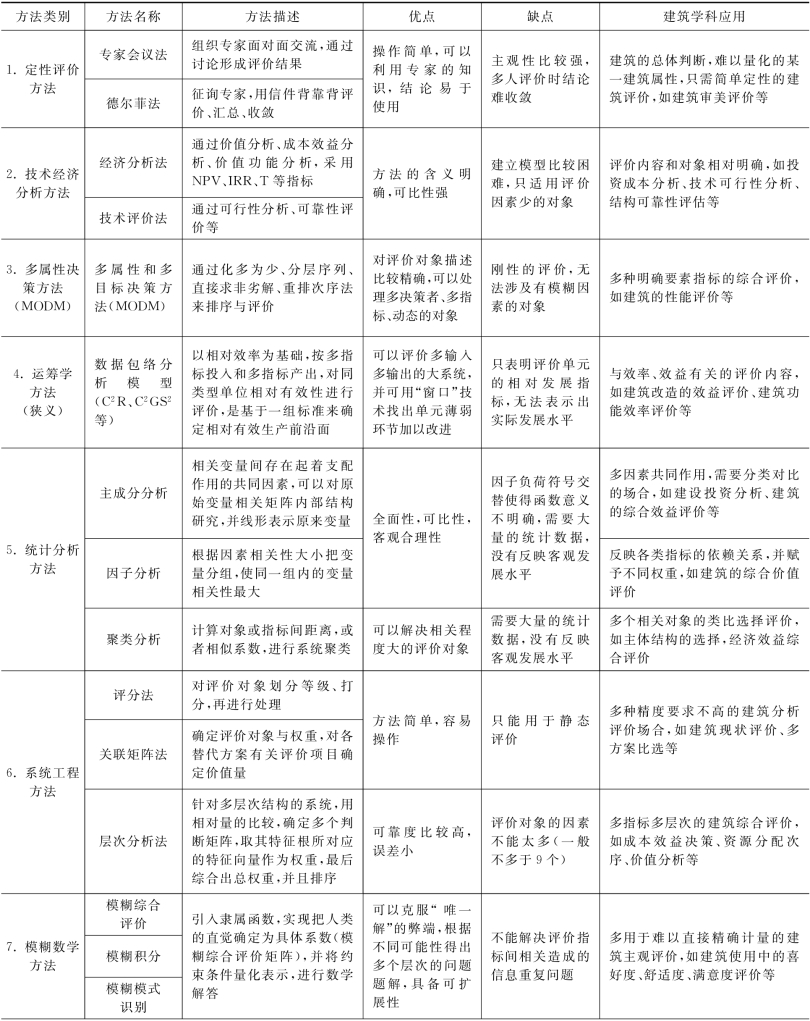
续表1－1

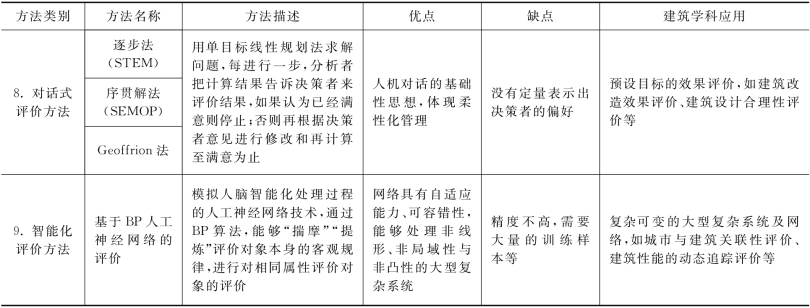
资料来源：修改整理自：陈衍泰，陈国宏，李美娟.综合评价方法分类及研究进展［J］.管理科学学报，2004，7（2）：69－79

其中，以下几种方法在建筑学科研究领域得到较多的应用：

1）综合评分法

综合评分法适用于评价指标无法用统一的量纲进行定量分析的场合，而用无量纲的分数进行综合评价。首先为需要作出评价的对象选定评价的具体指标，并制定出评分表，内容包括所有评价指标及其等级区分和评分规则；其次，评价者收集和指标相关的资料，根据指标和等级评出分数值，并填入表格；最后进行数据处理与评价，将各个指标所得分值进行综合整理归纳，计算各组的综合评分和评价对象的总评分，并按原先确定的评价目的予以运用。归纳来说，综合评分法简便易行，在定性为主的评价中应用较广。(www.xing528.com)

2）模糊综合评价法

模糊综合评价法是一种基于模糊数学^[8]的综合评标方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰、系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种非确定性问题的解决。进行模糊综合评价时，首先建立评价因素集，对各评价因素选择适当的标准，在对每个评价因子进行单项评价的基础上，给出各单项因子隶属于各级标准的隶属度，并根据各评价因素对评价结果的不同影响确定权重，然后进行模糊转换，求得最终的综合评价结果，即隶属于某一标准的隶属度。模糊评价法不仅可对评价对象按综合分值的大小进行评价和排序，还可根据模糊评价集上的值按最大隶属度原则去评定对象所属的等级。模糊综合评价法的优势在于分辨性与可比性较强，但是其运用了模糊数学的原理及方法，过程复杂且不易掌握。

3）层次分析法（Analytic Hierarchy Process，简称AHP）

美国运筹学家、匹兹堡大学萨迪教授（T.L.Saaty）于1977年在第一届国际数学建模会议上宣读了《无结构决策问题的建模——层次分析法》一文，宣告一种新的决策方法问世。所谓层次分析法，是指将一个复杂的多目标决策问题作为一个系统，将目标分解为多个目标或准则，进而分解为多指标（或准则、约束）的若干层次，通过定性指标模糊量化方法算出层次单排序（权数）和总排序，以作为目标（多指标）、多方案优化决策的系统方法。层次分析法的基本特征，其一是要有一个属性集的层次结构模型，它是层次分析法赖以建立的基础；其二是针对上一层某个准则，把下一层与之相关的各个不可公度的因素，通过对比，按重要性等级赋值，从而完成从定性分析到定量分析的过渡。归纳来说，AHP是分解、判断与综合的产物，是一种定性与定量相结合、将人的主观判断用数量形式表达和处理的方法。AHP的层次结构关系，可分为总目标层（综合指标层）、准则层（一级指标）、指标层（二级指标）以及因子层，见图1－3。

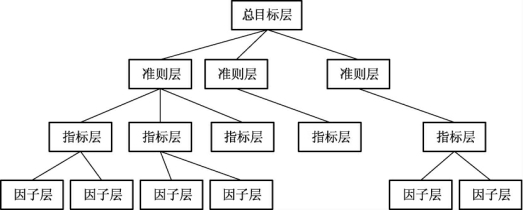
图1－3　评价指标层次结构模型

图片来源：笔者绘制

本书在评价研究中根据具体情况综合运用了多种评价方法：在构建建筑遗产保护利用综合评价指标体系时主要采用层次分析法，其简洁明了并将复杂问题简单化，从评价指标的选取、体系的构建到指标权重的分配，层次结构分明，使得整个评价工作更为系统化、客观化与科学化；在评价指标中无法用统一的量纲进行分析时，尤其是一些主观层面的评价指标，结合德尔菲法与综合评分法进行分级打分评价；在评价对象及其指标较为模糊并难以精确量化时，如涉及建筑遗产的多元价值、再利用适用性等指标，则使用模糊综合评价的方法，通过模糊转换等求得隶属度和评价结果。