岩土工程所面临的对象是复杂的地质体。这些复杂的地质体在一定时间和一定的条件下，可能处于相对稳定的平衡状态。如果条件改变，原来的平衡状态就有可能遭到破坏。隧道施工过程中，原有的应力场会重新分布，从而使岩土体发生变形，进而产生塌陷、滑坡或地面沉降等地质灾害。为预防和治理这些地质灾害，工程上常会采用一些支护手段，如临时支撑、永久性衬砌、锚杆、土钉等。用于调动和提高岩土材料的自身强度和自稳能力。对于隧道工程中的锚喷支护的力学机理，一般从围岩和锚喷支护共同作用的观点出发，认为支护不仅承受来自围岩的压力，并且反过来也给围岩以压力，改善围岩的受力状态，限制围岩的变形；同时还认为施加了锚喷支护以后，可以提高围岩的强度指标，从而提高围岩的承载能力（胡国伟等，2007）。进行有限元分析时，通常有以下两种处理方法。
（1）提高锚喷加固区的围岩参数（如弹性模量及C′、φ′等）来模拟锚喷支护的作用。但这种处理方法的问题在于，无法分析锚杆和喷层本身的受力特性及其失效后对围岩的影响。
（2）将锚杆处理成铰接于岩石单元节点的杆单元（一维轴力单元），锚杆的作用视为对围岩内壁增加附加抗力Pa。
从考虑单根锚杆出发，导出锚杆的静力平衡方程。如图7-2所示，拉力作用于锚杆时，锚杆受拉伸长，并通过界面将力传给灌浆和岩体。于是锚杆与砂浆界面以及砂浆与岩体界面产生切应力，在z—z+Δz微段内的传递用下式表示：
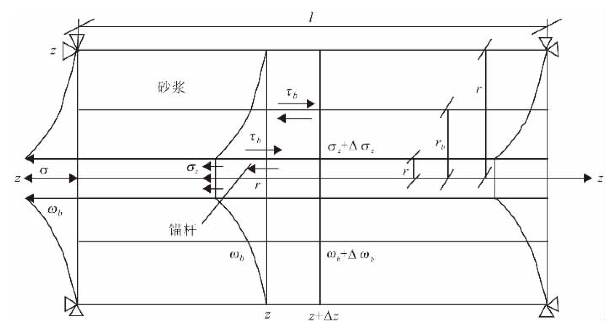
图7-2 锚杆受力示意图
式中：τb为锚杆砂浆界面的切应力：
rb为锚杆半径；
σz为锚杆轴向应力。
假设锚杆为弹性状态，利用胡克定律可以导出：
式中：ωb为锚杆及锚杆砂浆界面沿z方向的变位；
Eb为锚杆拉伸弹性模量；
εz为锚杆轴向应变。
另外，也可以得到径向平衡方程：
式中：τrz为垂直径向柱面上沿z方向切应力。(www.xing528.com)
有了锚杆轴向、径向平衡式，很容易进行有限元离散。式（7-16）在边界条件上有：
可以写成：
分部积分，得：
对z方向变位ω及试验函数Φ进行离散近似：
式中
为各节点z方向变位
）为r方向形函数
为z方向形函数。
将式（7-20）和式（7-21）代入式（7-19）得到：
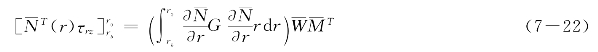
式（7-22）即为锚杆径向的有限元离散化方程。
对于一维线性单元e，设其两端节点分别为s和t，则形函数
可以写成：式中：he=rt-rs。
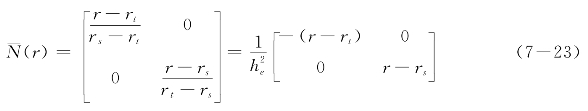
同样，也可以得到锚杆轴向的有限元离散化方程：
对于一维线性单元e，设其两端节点分别为p和q，其形函数如下：
其中，le=zq-zp。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
