改进粒子群算法MPSO在求解非线性方程组中的应用

（1）问题转化

通常情况下，包含n个变量的m个方程的方程组的一般形式为：

其中，ai≤xi≤bi，i=1，2，…，n。

在运用优化解法求解时，应将代数方程组转化为优化问题，即式（6.6）。当F（X）最小值为0时，所对应的X即为方程组（6.6）的解，于是方程组求解问题转化为函数优化问题。在应用时，往往当F（X）最小值满足求解误差的要求时，所对应的X即可作为方程组的解。

其中，X=（x1，x2，…，xn），X∈S={（x1，x2，…，xn）|ai≤xi≤bi}，δi＞0为权值，表示每个方程在目标函数中的权重，‖·‖为向量范数，常用1范数和2范数。本文取δi=1，i=1，2，…，m，且选用1－范数，即：

（2）算法流程

MPSO算法步骤如下。

Step 1，在初始化范围内，对粒子群（种群规模为N）中各粒子进行速度和位置随机初始化，为了保证种群多样性，将所有粒子位置均匀分布在搜索区域内，粒子位置按式（6.8）进行初始化：(www.xing528.com)

其中，R为［0，1］之间均匀分布的随机数，i=1，2，…，N，j=1，2，…，D。

Step 2，计算所有粒子的适应值。

Step 3，根据粒子群当前状态，更新每个粒子所经历的最好位置pbest和所有粒子所经历的最好位置gbest。

Step 4，根据式（6.9）计算惯性权重，按式（6.10）和式（6.2）对粒子的速度和位置进行更新，用式（6.3）和式（6.4）进行越界限制。

Step 5，当迭代次数未达到最大迭代次数itmax时，则转Step2；若达到最大迭代次数，则进行Step6。

Step 8，在（－Bk，Bk）上按照均匀分布产生一个随机数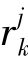，令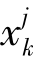=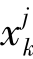+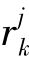，计算F2=F（xj）；如果F2≥F1，则令，返回Step7，否则令F1=F2，k=k+1；如果k＞D，令k=1，j=j+1，，k=1，2，…，D。

Step 9，检查是否达到预设精度ε和最大迭代次数，如未达到，且j＜104，则返回Step7，否则，将作为min F（X）最终数值解。