混杂系统建模方法在高地应力硬岩诱导卸荷

（1）混杂Petri网建模方法

为了对混杂系统进行分析和研究，需要有能够很好地描述其特性的模型。混杂Petri（HybridPetriNets，HPN）网的概念由David和Alla在1992年提出，将离散事件系统和连续时间系统在同一层次直接交互。现有基于混杂Petri网的建模方法主要有：

依据数学模型（微分方程）来建立混杂Petri网模型。在同一层次上对连续部分和离散部分建模，连续库所表示系统的状态变量，离散库所表示装置的状态。

Petri网模型和微分方程组相结合的方法。Petri网模型用来描述离散部分，微分方程组用来描述连续部分，这两部分的接口通过积分器来实现。这种方法可以充分利用已经发展成熟的Petri网理论和连续动态系统理论。

分层递阶建模方法。该方法将一个复杂问题分成几个子问题来解决，降低了建模难度，通常将整个系统分解成基本的控制层、协调层和监督管理层，再对各层采用相应的模型来描述。

（2）混杂Petri网基本理论

标记的混合Petri网是一个六元组Q=〈P，T，Pre，Post，h，M0〉其中：

P=PC∪PD={P1，P2，…，Pn}（n≥0）有限非空库所集。

T=TC∪TD={T1，T2，…，Tm}（m≥0）有限非空变迁集。

Pre：P×T→R+（N）输入关联映射，表示输入库所与变迁之间的有向弧权重。

Post：P×T→R+（N）输出关联映射，表示变迁与输出库所之间的有向弧权重。

h：P∩T→{D，C}混合函数，指明结点是离散节点（PD和TD）还是连续节点（PC和TC）。

M0：P→R+（N）初始标识。

如果Pi∈PD，，则Pre，Post，M0取值范围为N。

如果Pi∈PC，则Pre，Post，M0取值范围为R+。

Pre，Post满足准则：(www.xing528.com)

如果Pi∈PD，且Tj∈TC，则Pre（Pi，Tj）=Post（Pi，Tj）。

在混杂Petri网的图形中，如图6.8所示，分别表示了HPN的各个节点。其中，双圈表示连续位置，单圈表示离散位置；用空心条表示连续变迁，实心条表示离散变迁。对其输入输出弧、权重标记、变迁标记等描述中，都有一些比传统的离散Petri网更深刻的内容，用以描述连续变迁、离散变迁、连续到离散、离散到连续等状态演变。

图6.8　HPN节点表示

满足下列条件，称一个变迁Tj是使能的：

如果Tj是离散变迁，那么对任何Pi∈°Tj满足条件：

M(Pi)≥Pre(Pi，Tj)

这里对离散变迁的输入集和输出集的元素没有任何限制，即不区分离散库所和连续库所。

如果Tj是连续变迁，那么对任何Pi∈°Tj满足条件：

对∀∈°Tj，有M（Pi）≥Pre（Pi，Tj）。

对∀∈°Tj，有M（Pi）＞0或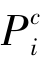是被供给的。

对于连续变迁，当∃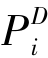∈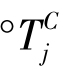时，必有∈（）°。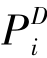

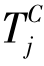使能的连续变迁有强使能和弱使能之分。如果°Tj中的每个连续库所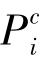都满足M（Pi）＞0，则这个变迁是强使能的，否则，是弱使能的。

根据混合Petri网的定义，一个连续变迁的激发不能改变离散库所中的标识，只能读取离散库所中的内容，这使得连续的行为能被离散标识所修改。

一个离散变迁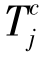的激发包括从每个输入库所Pi中取出Pre（Pi，Tj）个标记，而在每个输出库所Pk中增加Post（Pk，TJ）个标记，一个激发量为r的连续变迁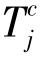的激发，包括从每个输入位置Pi中取出量为r×Pre（Pi，Tj）个标记，而在每个输出库所Pk中增加量为r×Post（Pk，Tj）个标记。