解压缩弹簧时外力做功全部转化为势能

典型例题

例1　一个人在岸上以速度ν水平拉船，岸的高度为h，绳子与河面夹角为θ，此时船的速度和加速度为多少？

（2017清华大学）

例2　如图所示，光滑导轨上垂直放置两根质量为m且有电阻的金属棒，导轨宽处与窄处间距比为2：1，平面内有垂直纸面向内的磁场。现给左边的杆一个初速度ν0，在系统稳定时，左杆仍在宽轨上，右杆仍在窄轨上运动，则这个过程产生的热量Q为多少？

（2016清华大学）

解　当系统稳定时，导轨不再受磁场力，此时无感应电流，两导轨匀速运动导致磁通量变化为零，满足以上条件，需要左右两导轨速度比为1：2，则：根据两导轨系统动量守恒：mν0＝mν1＋mν2。磁通量不变（或切割磁感线产生的动生电动势等大）：l1ν1＝l2ν2。

例3　在光滑的水平面上有一质量为M、倾角为θ的光滑斜面，其上有一质量为m的物块，如图所示。物块在下滑的过程中对斜面压力的大小为（　）

（2011北京大学）

解　设物块对斜面的压力为N，物块m相对斜面的加速度为a1，斜面的加速度为a2，方向向左；则物块m相对地面的加速度为aχ＝a1cosθ﹣a2，ay＝a1sinθ，由牛顿第二定律对m有

例4　在光滑的水平桌面上有两个质量均为m的小球，由长度为2l的拉紧细线相连。以一恒力作用于细线中点，恒力的大小为F，方向平行于桌面。两球开始运动时，细线与恒力方向垂直。在两球碰撞前瞬间，两球的速度在垂直于恒力方向的分量为（　）

（2010清华大学）

解　设两球的速度沿恒力方向的分量为νχ，在垂直于恒力方向的分量为νy，在两球碰撞前的瞬间，两球的速度的两个分量大小相等，即νχ＝νy，恒力F的位移为2l，由动能定理得

例5　如图，一简谐横波沿χ轴正方向传播，图中实线为t＝0时刻的波形图，虚线为t＝0.286 s时刻的波形图，则该波的周期T和波长λ可能正确的是（　）

A.0.528 s　2 m

B.0.528 s　4 m

C.0.624 s　2 m

D.0.624 s　4 m

（2012清华大学）

例6　如图甲，在χOy平面内有一列沿χ轴传播的简谐横波，频率为2.5 Hz。在t＝0时，P点位于平衡位置，且速度方向向下，Q点位于平衡位置下方的最大位移处。则在t＝0.35 s时，P、Q两质点的（　）

A.位移大小相等，方向相反

B.速度大小相等，方向相同

C.速度大小相等，方向相反

D.加速度大小相等，方向相反

解　T＝0.4 s，在t＝0时的波形如图乙所示。由波的周期性，t＝0.35 s＝时的波形与t＝﹣时的波形相同，如图乙虚线所示，可见选项ABD正确。

例7　如图所示，竖直墙面和水平地面均光滑，质量分别为mA＝m，mB＝3m的A、B两物体如图所示放置，其中A紧靠墙壁，A、B之间有质量不计的轻弹簧相连，现对B物体缓慢施加一个向左的力，该力做功W，使A、B间弹簧被压缩但系统静止，最后突然撒去向左推力解除压缩。求：

（1）从撒去外力到物块A运动，墙壁对物块A的冲量大小？

（2）A、B都运动后，A、B两物的最小速度各为多大？

（2011清华大学）

解　（1）压缩弹簧时外力做功全部转化为势能，撒去外力后，物体B在弹力作用下加速运动。在弹簧恢复原长的过程中，系统的机械能守恒。设弹簧恢复原长时，物体B的速度为νB0，有解得

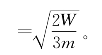
在此过程中，墙对A的冲量大小等于弹簧对A的冲量的大小，也等于弹簧对B的冲量大小，则联立解得

（2）当弹簧恢复原长后，物体A的速度从最小值逐渐增大νA，有νA＝0。物体A离开墙壁后，弹簧伸长，物体A的速度逐渐增大，物体B的速度逐渐减小。当弹簧恢复到原长时，物体A达到最大速度νA，物体B的速度减小到最小值νB，在此过程中系统的动量守恒、机械能守恒，有

例8　如图所示，小球从台阶上以一定初速度水平抛出，恰好落到第一级台阶边缘，反弹后再次落下经0.3 s后恰好落至第3级台阶边界，已知每级台阶宽度及高度均为18 cm，取g＝10 m/s2，且小球反弹时水平速度不变，竖直速度反向，但变为原速度的(www.xing528.com)

（1）求小球抛出时的高度及距第一级台阶边缘的水平距离；

（2）问小球是否会落到第5级台阶上？说明理由。

（2012清华大学）

例9　（1）质量约为1 T的汽车在10 s内由静止加速到60 k m/h。如果不计阻力，发动机的平均输出功率约为多大？

（2）汽车速度较大时，空气阻力不能忽略。将汽车简化为横截面积约1 m2的长方体，并以此模型估算汽车以60 k m/h行驶时为克服空气阻力所增加的功率。已知空气密度ρ＝1.3 kg/m3。

（3）数据表明，上述汽车所受阻力与速度的平方的关系如图所示。假定除空气阻力外，汽车行驶中所受的其他阻力与速度无关，估计其他阻力总的大小。

（2013清华大学）

解　（1）假设汽车启动时做匀加速运动，根据匀加速运动规律有

在不计阻力的情况下，汽车的平均功率为

联立①②③式并代入数据解得

（2）假设汽车的横截面积为A，当汽车以一定速度运动时，将推动前方的空气使之获得相应的速度，则在∆t时间内，车前方以A为底、ν·∆t为高的柱形空气获得的动能为

为使该空气柱在∆t时间内获得上述动能，车需增加的功率为

根据已知条件，汽车的横截面积约为1 m2，代入上式解得

（3）当汽车匀速运动时，牵引力与阻力平衡，由图可知

式中F为牵引力，f为除空气阻力外的其他阻力之和，外推图线得

例10　明理同学平时注意锻炼身体，力气较大，最多能提起m＝50 kg的物体。一重物放置在倾角为θ＝15°的粗糙斜坡上，重物与斜坡间的摩擦因数为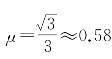。试求该同学向上拉动的重物质量M的最大值。

（2013清华大学）

解　如图所示，设该同学拉动重物的力F的方向与斜面所成的角度为ψ，根据力的平衡，在垂直于斜面的方向上有FN＋F sinψ﹣Mgcosθ＝0。①

式中FN是斜面对重物的支持力，其大小等于重物对斜面的正压力。

例11　平直铁轨上停着一节质量为M＝2m的小车厢，可以忽略车厢与水平铁轨之间的摩擦。有N名组员沿着铁轨方向列队前行，另有1名组长在最后，每名组员的质量同为m。

（1）当组员和组长发现前面车厢时，都以相同速度ν0跑步，每个组员在接近车厢时又以2ν0速度跑着上车坐下，组长却因跑步速度没有改变而恰好没有追上车，试求N。

（2）组员们上车后，组长前进速度减为，车上的组员朝着车厢前行方向一个接一个水平跳下，组员离开车的瞬间的速度与车厢速度相同为u，结果又可使组长也能追上车。试问，跳车过程中组员们总共至少消耗掉人体中的多少内能？

（2011清华大学）

例12　两质量均为m的小球，放在劲度系数为k，原长为L的弹簧两端，自由静止释放。设两个小球中心与整个弹簧都始终在一条直线上。（小球半径r≪L）

（1）问仅在两球之间万有引力的作用下，弹簧的最大压缩量χ为多大？

（2）若体系整体绕中心以角速度ω旋转，要求弹簧保持原长，角速度ω应为多大？

（2009同济大学）

例13　图所示是传送带装置，与水平面的夹角为θ，且tanθ＝0.75。传送带的速度为ν＝4 m/s，动摩擦因数为将一个质量m＝4 kg的小物块轻轻地放置在装置的底部，已知传送带装置的底部到顶部之间的距离L＝20 m。（本题重力加速度g＝10 m/s2）

（1）求物块从传送带底部运动到顶部的时间t；

（2）求此过程中传送带对物块所做的功。

（2014清华大学）