高校自主招生：平面向量与复数的拓展知识

复数的几何意义

复数z＝a＋b i（a、b∈R）与有序实数对（a，b）是一一对应的关系。这是因为对于任何一个复数z＝a＋b i（a、b∈R），由复数相等的定义可知，可以由一个有序实数对（a，b）唯一确定，如z＝3＋2i可以由有序实数对（3，2）确定，又如z＝﹣2＋i可以由有序实数对（﹣2，1）来确定；又因为有序实数对（a，b）与平面直角坐标系中的点是一一对应的，如有序实数对（3，2）与平面直角坐标系中的点A（3，2）是一一对应的。由此可知，复数集与平面直角坐标系中的点集之间可以建立一一对应的关系。

典型例题

例1　已知实数a，b满足：（a2＋4）（b2＋1）＝5（2ab﹣1），则的值为（　）

（2017北京大学博雅计划）

所以∣f（χ）∣＜2，即函数f（χ）的值域为（﹣2，2）。

例11　已知χ，y∈（0，1），且3χ＋7y，5χ＋y均为整数，则这样的（χ，y）共有________对。

（2014南开大学）

解　设3χ＋7y＝u，5χ＋y＝ν，因为χ，y∈（0，1），所以可得u∈{1，2，3，4，5，6，7，8，9}，ν∈{1，2，3，4，5}。

又由3χ＋7y＝u，5χ＋y＝ν可得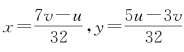，结合χ，y∈（0，1）可得0＜7ν﹣u＜32，0＜5u﹣3ν＜32。

经验证：ν＝1时，u＝1，2，3，4，5，6；ν＝2时，u＝2，3，4，5，6，7；ν＝3时，u＝2，3，4，5，6，7，8；ν＝4时，u＝3，4，5，6，7，8；ν＝5时，u＝4，5，6，7，8，9。

综上，满足条件的（u，ν）有31对，即满足条件的（χ，y）有31对。

例12　求方程2χ﹣5y·7z＝1的所有非负整数解（χ，y，z）。

（2016中国科学技术大学）

解法一　由题设可得（﹣1）χ﹣（﹣1）y≡1（mod 3），所以χ是奇数，y是偶数。

可设χ＝2m＋1，y＝2n（m，n∈N），使得原方程变为2×4m﹣25n×7z＝1。

若n∈N＊，可得2（﹣1）m＝﹣2≡1（mod 5），这是不可能的，所以n＝0，y＝0。

从而原方程化为2×4m﹣7z＝1。

（1）当z＝0时，得m＝0，此时得一组解为（1，0，0）；

（2）当z∈N＊时，得﹣（﹣1）z≡1（mod 4），所以z是正奇数，设z＝2p＋1（p∈N）

从而原方程化为2×4m﹣7×49p＝1。

①当p＝0时，得m＝1，此时得一组解为（3，0，1）；

②当p∈N＊时，得m≥4，所以﹣7×1p≡1（mod 16），由于71≡7，72≡1（mod 16），所以7z≡﹣1（mod 16）不可能的。

综上所述，可得原方程的所有非负整数解只有（χ，y，z）＝（1，0，0），（3，0，1）。

解法二　因为2χ＝5y·7z＋1，从而5y·7z＋1是偶数，所以χ≥1。则5∣2χ﹣1，χ是4的倍数，但此时2χ﹣1被3整除，与题意不符合，所以y＝0。故原方程为2χ﹣1＝7z。

当χ＝1时，z＝0；

当χ＝2时，无解；

当χ＝3时，z＝1；

当χ≥4时，7z≡﹣1（mod 16）。但71≡7，72≡1（mod 16），所以7z≡﹣1（mod 16）是不可能的。

所以，原不定方程的所有非负整数解只有（χ，y，z）＝（1，0，0），（3，0，1）。

例13　求所有的函数f：N＊→N＊，使得对任意正整数χ≠y，0＜∣f（χ）﹣f（y）∣＜2∣χ﹣y∣。

（2016中国科学技术大学）

解法二　在题设所给的不等式中，可令y＝χ＋1（χ∈N＊），得0＜∣f（χ＋1）﹣f（χ）∣＜2。

即∣f（χ＋1）﹣f（χ）∣＝1。

对任意正整数χ≠y，0＜∣f（χ）﹣f（y）∣，即f（χ）≠f（y），从而f（χ）是单射，

所以f（χ＋1）﹣f（χ）≡1或f（χ＋1）﹣f（χ）≡﹣1（否则必然会出现不同的自变量被映射到同一个正整数的情形）。

因为象的集合为N＊，所以f（χ＋1）﹣f（χ）≡1，进而可得

f（n）＝n﹣1＋f（1），则f（χ）＝χ＋t﹣1（χ∈N＊，f（1）＝t∈N＊）。

例14　甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内任何时刻到达是等可能的。

（1）如果甲船和乙船的停泊时间都是4小时，求它们中的任何一条船不需要等待码头空出的概率；

（2）如果甲船的停泊时间为4小时，乙船的停泊时间是6小时，求它们中的任何一条船需要等待码头空出的概率。

（2017山东大学）

例15　已知sin A＋sin B＋sin C＝0，cosA＋cosB＋cosC＝0。

求证：sin3A＋sin3B＋sin3C＝3sin（A＋B＋C）；cos3A＋cos3B＋cos3C＝3cos（A＋B＋C）。

（2017南京大学）

真题链接

一、选择题

1.函数

，χ∈［﹣1，2］上的最大值与最小值的差所在的区间是（　）

A.(2，3)

B.(3，4)

C.(4，5)

D.前三个答案都不对

（2017北京大学博雅计划）

2.设整数a、m、n满足，则这样的整数组（a，m，n）的个数为（　）

A.0

B.1

C.2

D.前三个答案都不对

（2017北京大学博雅计划）

3.满足f（f（χ））＝f4（χ）的实系数多项式f（χ）的个数为（　）

A.2

B.4

C.无穷多

D.前三个答案都不对

（2017北京大学博雅计划）(www.xing528.com)

4.已知三角形三条中线的长度分别为9、12、15，则该三角形的面积为（　）

A.64

B.72

C.90

D.前三个答案都不对

（2017北京大学博雅计划）

5.方程log4（2χ＋3χ）＝log3（4χ﹣2χ）的实根个数为（　）

A.0

B.1

C.2

D.前三个答案都不对

（2017北京大学博雅计划）

6.设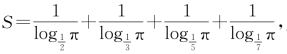则不超过S，且与S最接近的整数为（　）

A.﹣5

B.4

C.5

D.前三个答案都不对

（2017北京大学博雅计划）

7.已知复数z满足是实数，则∣z＋i∣的最小值等于（　）

（2017北京大学博雅计划）

8.已知正方形ABCD的边长为1，P1、P2、P3、P4是正方形内部的4个点，使得△ABP1、△BCP2、△CDP3、△DAP4都是正三角形，则四边形P1P2P3P4的面积等于（　）

（2017北京大学博雅计划）

9.已知某个三角形的两条高线的长度分别为10和20，则它的第三条高线长度的取值区间为（　）

（2017北京大学博雅计划）

10.正方形ABCD与点P在同一个平面内，已知该正方形的边长为1，且∣PA∣2＋∣PB∣2＝∣PC∣2，则∣PD∣的最大值为（　）

（2017北京大学博雅计划）

11.使得p3＋7p2为平方数，且不大于100的素数p的个数为（　）

A.0

B.1

C.2

D.前三个答案都不对

（2017北京大学博雅计划）

二、填空题

1.方程＝sinχ有________个解。

（2017中国科学技术大学）

2.已知集合A＝{1，2，3，4，5}，映射f：A→A，且f即是单射又是满射，满足f（χ）＋f（f（χ））＝6恒成立，则f（1）＝________。

（2017中国科学技术大学）

3.正方体的十二条棱中，取四条两两不相交的棱，有________种取法。

（2017中国科学技术大学）

4.已知复数z满足则复数z的实部的最小值为________。

（2017中国科学技术大学）

5.整数χ、y满足∣χ∣＋∣y∣≤n（n∈N），满足条件的整数对（χ，y）有________组。

（2017中国科学技术大学）

三、解答题

1.在△ABC中，角A、B、C所对的边分别为a、b、c，满足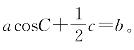

（1）求角A；

（2）若a＝1，求三角形内切圆半径R的最大值。

（2017山东大学）

2.数列{an}满足：

（1）求数列{an}的通项公式an；　（2）求证：

（2017山东大学）

3.已知抛物线C：y2＝2pχ，点A（a，b），B（﹣a，0）。若M为抛物线C上任意一点，直线MA、MB与抛物线C的另一个交点分别为M1，M2，求证：直线M1M2过定点。

（2017山东大学）

4.已知

（1）若在（0，1）处的切线与y＝f（χ）的图象仅有一个交点，求m的值；

（2）证明：f（χ）存在单调递减区间［a，b］，并求t＝b﹣a的取值范围。

（2017山东大学）

5.在Rt△ABC中，a≤b≤c，若，求M的最大值。

（2017山东大学）

6.已知椭圆C：，双曲线T：χy＝4。

（1）求椭圆C上一点M处的切线方程；

（2）若点P在椭圆C上，Q在双曲线T上，求证：

（2017中国科学技术大学）

7.已知0＜ai＜bi＜1对i∈［1，2 017］（i∈N）恒成立，且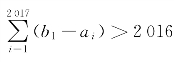，求证：存在实数χ，使得ai＜χ＜b1对i∈［1，2 017］（i∈N）恒成立。

（2017中国科学技术大学）