先进汽车缓速器设计与试验

为了研究液冷式永磁缓速器的结构参数对其制动力矩的影响，本书应用试验设计法和Rosenbrock法进行永磁缓速器电磁场模型的优化设计。图6-31所示为永磁缓速器电磁场分析模型，从图中可看出各尺寸参数。由于对称边界条件，只建立了1/20的模型。转子和永磁体以750r/min的转速旋转。用Rosenbrock法使图中的永磁缓速器制动力矩得以优化，即在一定转速下，使制动功率P与永磁体体积V之比达到最大值，同时，定子不会出现过热现象而导致永磁体失磁。

图中4个设计参数（h₁是转子厚度；h₂是定子厚度；h_m是永磁体厚度；b_m是永磁体宽度）是未知变量，需要优化。永磁体体积V为

V=h_mb_mL_m（m³） （6-27）

式中，L_m是永磁体厚度。

对该模型进行优化，使目标函数W变得最小，见式（6-28）。为了避免制动功率过大而导致永磁体失磁，定子中涡流密度J_s的最大值必须小于指定值J_s0=2.5×10⁸A/m²。

图6-31 永磁缓速器电磁场分析模型

式中，U是罚函数，定义如下

J_s的计算公式为

式中，J_sx、J_sy和J_sz是复数。因此式（6-28）可以近似为

表6-7给出了缓速器优化设计尺寸的初始值及其约束条件。

表6-7 缓速器优化设计尺寸的初始值及其约束条件

采用试验设计法，根据表6-8选择一个3水平4因素的试验确定初选尺寸参数，因此要选用L₉（3⁴）来安排试验。制动力矩有总共要做9个试验，从表6-8中所示的正交阵列计算得到。1～3号试验有h₁的一个级别1。级别1的有效值是1～3号模型的平均值。级别2和级别3的有效值分别是4～6号模型和7～9号模型的平均值。初始值和约束可以通过每个设计变量对转矩的影响来确定，如图6-32所示。通过如下方法确定：

1）通过比较每个级别的制动力矩来减少搜索区域。在工况2中，如果级别1最大，级别2较小，级别3最小，则认为最佳值小于级别2。同理，认为工况3的最佳值大于级别1，小于级别3。如果变量灵敏度设计的较低，如工况1，则最优值的搜索区域不能减少。

2）制动力矩达到最大极限值时，设计变量的级别可以采用一个备选最佳值，或者为最大力矩时的设计变量选取多级别组合值。

表6-8 优化试验方案

图6-32 设计变量的影响(www.xing528.com)

通过试验设计法优化后的结果见表6-9所示，用该种方法得到了初步的优化尺寸参数。

表6-9 试验设计法优化结果

注：1.使用的计算机：AMD Opteron Processor 61282.0GHz，8核；

2.RBM收敛标准：0.3mm；

3.ICCG方法的收敛标准：5×10^-4。

Rosenbrock法是一种迭代法，用于获得尺寸的最佳值。因为不必用目标函数W的梯度，所以这种方法很容易与有限元法结合。在执行这种方法的过程中，取W的最大值作为最佳值时，要以步长ΔL来改变L。步长初始值ΔL^（0）取自初始形状尺寸的1/10。

当搜索成功（W变大时），第（k+1）次的长度ΔL^（k+1）变成式（6-32）

ΔL^（k+1）=α·ΔL^（k） （6-32）

当搜索不成功（W变小）时，ΔL^（k+1）变成式（6-33）

ΔL^（k+1）=-β·ΔL^（k） （6-33）

式中，α和β是ΔL的调节系数，取值分别为2和0.5。如果ΔL足够小，则搜索结束，得出缓速器的最佳尺寸。

图6-33给出了Rosenbrock法优化设计流程图。使用Rosenbrock法和试验设计法的优化过程如下。

1）使用有限元法和试验设计法进行磁场计算获得初始尺寸。

2）计算目标函数W。

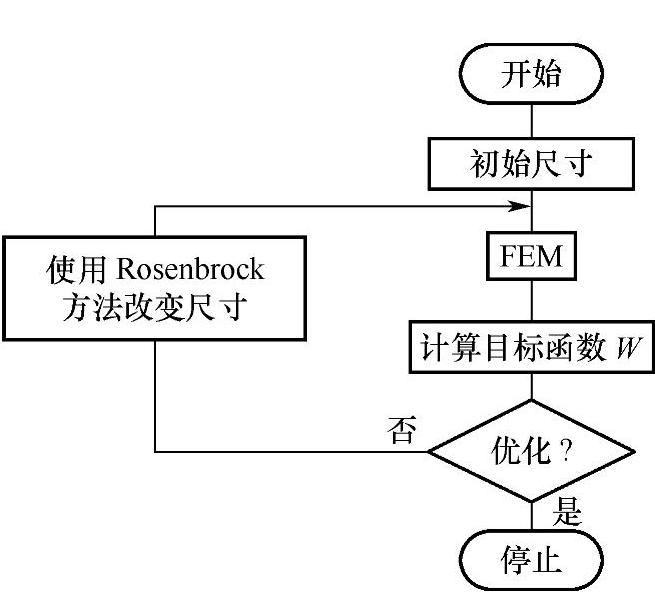
图6-33 Rosenbrock法优化设计流程图

3）改变尺寸，采用Rosenbrock法，并考虑约束条件。

4）重复进行2）～3）步的计算过程，直到获得缓速器的最佳尺寸。

通过Rosenbrock法优化后的结果见表6-10，用该种方法得到了精确的优化尺寸参数。优化后的永磁体质量减小了22%，定子和转子的质量也减小了约16%，制动力矩仅减小了4.5%。

表6-10 Rosenbrock法优化结果